当前位置：首页 > news >正文

牛客周赛 Round 111(小红的阶梯/小红的数组取数/小红抽卡/小红的好数对/小芳的排列构造小红的排列构造)

news 2025/9/29 13:51:49

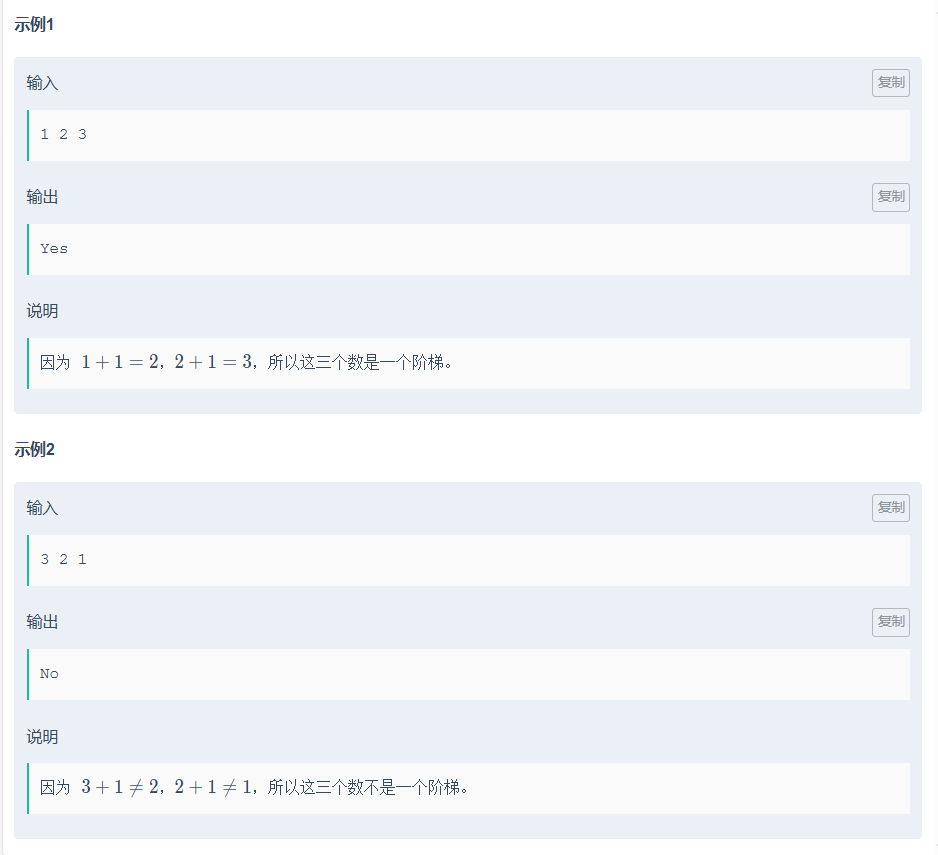
小红的阶梯

#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
void solve() {int x, y, z;cin >> x >> y >> z;if (x + 1 == y && y + 1 == z) {cout << "Yes" << endl;}else {cout << "No" << endl;}return;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步std::cin.tie(nullptr),std::cout.tie(nullptr);             // 解除cin与cout绑定int t = 1;//cin >> t;while (t--) {solve();}return 0;
}

小红的数组取数

思路：

就是找a数组的最小值位置和b数组最大值的位置。

#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
void solve() {int n;cin >> n;vector<int>a(n), b(n);int min_a=INT_LEAST32_MAX, aj = -1;for (int i = 0; i < n; i++) {cin >> a[i];if (min_a > a[i]) {aj = i;min_a = a[i];}}int max_b = INT_LEAST32_MIN, bj = -1;for (int i = 0; i < n; i++) {cin >> b[i];if (max_b < b[i]) {bj = i;max_b = b[i];}}cout << aj + 1 << " " << bj + 1 << endl;return;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步std::cin.tie(nullptr),std::cout.tie(nullptr);             // 解除cin与cout绑定int t = 1;//cin >> t;while (t--) {solve();}return 0;
}

小红抽卡

思路：

x以下的数位置不变，x以上的数循环向右移一位。

所以可以将k先%x;

然后(x-k+i-1) % x+1，就是i位移k次后对应的坐标（a[1]为首元素）

#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
void solve() {ll n, k, x;cin >> n >> k >> x;vector<ll>a(n+1);for (int i = 1; i <= n; i++) {cin >> a[i];}k %= x;for (int i = 1; i <= n; i++) {if (i <= x) {cout << a[(x-k+i-1) % x+1] << " ";}else {cout << a[i] << " ";}}cout << endl;return;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步std::cin.tie(nullptr),std::cout.tie(nullptr);             // 解除cin与cout绑定int t = 1;//cin >> t;while (t--) {solve();}return 0;
}

小红的好数对

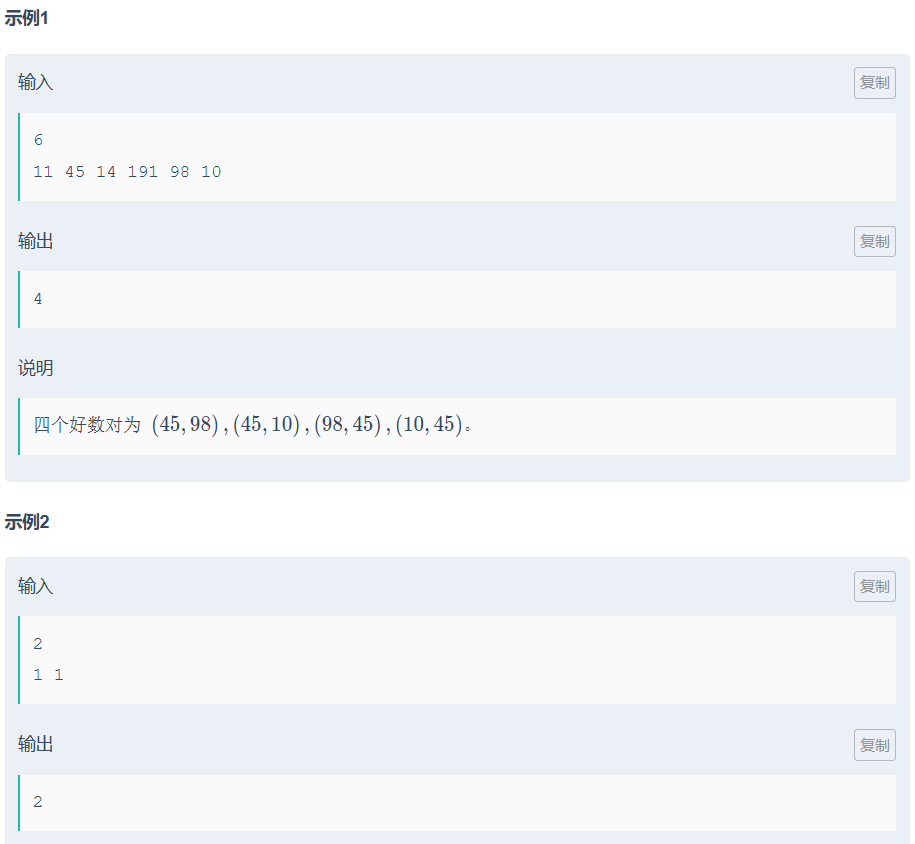
思路：

实现步骤

输入处理：读取数组并预处理每个数的模 11 结果及其不同位数下的模 11 结果(a[i]*10，a[i]*100……）
统计长度和模结果：使用二维数组 b 统计每个数的长度和模 11 结果的频率。
计算配对数量：遍历每个数，计算其作为 B 时满足条件的 A 的数量，注意避免重复计算和自配对。
输出结果：统计所有满足条件的数对数量。

预处理部分：
- 对每个数计算其模 11 的结果 a[i][0]。
- 计算其在不同拼接长度（1 到 9 位）下的模 11 结果 a[i][j]。
- 统计每个数的长度和模 11 结果的频率到二维数组 b 中。
配对条件检查：
- 对于每个数 B，计算其作为拼接后的数时需要的 A 的模 11 结果 required_mod。
- 查询 b 数组中满足条件的 A 的数量，并累加到答案中。
结果调整：
- 减去自配对的情况 sum，确保只统计不同元素的配对。

复杂度分析

时间复杂度：O(n * 9) = O(n)，每个数处理 9 次，适用于大规模数据。
空间复杂度：O(n + 11 * 11) = O(n)，预处理和统计数组的空间需求。

#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
void solve() {int n;cin >> n;vector<vector<ll>>a(n, vector<ll>(10)), b(11, vector<ll>(11));ll sum = 0;//记录能否与自己成对for (int i = 0; i < n; i++) {cin >> a[i][0];ll w = a[i][0];a[i][0] %=11;for (int j = 1; j <= 9; j++) {a[i][j] = a[i][j - 1] * 10 % 11;}int u = 0;ll o = 1;while (w > 0) {w /= 10;u++;o *= 10;}b[u][a[i][0]]++;if (a[i][0] * ((o + 1) % 11) % 11==0) {sum++;}}ll ans = 0;for (int i = 0; i < n; i++) {for (int j = 1; j <= 9; j++) {if (a[i][j] == 0) {ans += b[j][0];}elseans += b[j][11 - a[i][j]];}}cout << ans - sum << endl;return;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步std::cin.tie(nullptr),std::cout.tie(nullptr);             // 解除cin与cout绑定int t = 1;//cin >> t;while (t--) {solve();}return 0;
}

小芳的排列构造

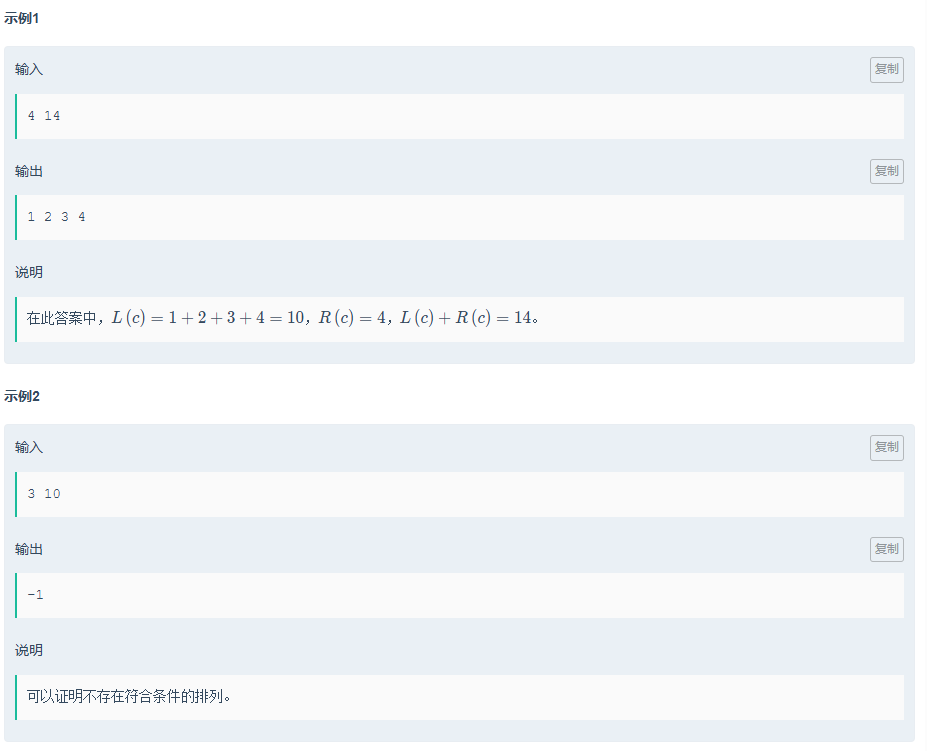
思路：

我可以发现L+R中 n必出现两次，n-1必出现一次，剩下的最多出现一次

所以n * (n + 1) / 2 + n < k||n*2+n-1>k 不存在

然后就找出1——n-2组成n的一种方案然后从小到大排列放在最前端就ok，剩下的放在n-1——n之间

#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
void solve() {ll n;ll k;cin >> n >> k;if (n == 1) {if (k == 2) {cout << 1 << endl;}else {cout << -1 << endl;}return;}vector<int>a(n + 1, 0);if (n * (n + 1) / 2 + n < k||n*2+n-1>k) {cout << -1 << endl;return ;}a[n] = 2, a[n - 1] = 2;k -= n * 2 + n - 1;int u = n - 2;while (k > 0) {if(k>u){k -= u;a[u--] = 1;}else {a[k] = 1;break;}}for (int i = 1; i <= n; i++) {if (a[i] == 1) {cout << i << " ";}}cout << n - 1 << " ";for (int i = 1; i <= n; i++) {if (a[i] == 0) {cout << i << " ";}}cout << n << endl;return;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步std::cin.tie(nullptr),std::cout.tie(nullptr);             // 解除cin与cout绑定int t = 1;//cin >> t;while (t--) {solve();}return 0;
}

小红的排列构造

思路：

这就有点相当与选择排序吧，将a[i]于j互换位置（a[i]==j),所以他最多就n-1步，最少是（n+1）/2步

关键观察

最小交换次数等于排列中环的个数减去1。对于排列a，可以将其分解为若干不相交的环。每个环需要至少（环长度-1）次交换才能将元素归位，总交换次数为n - c，其中c是环的个数。

因此，为了得到恰好k次交换，需要满足：

k = n - c
c = n - k

即排列必须恰好由（n - k）个环组成。

构造方法

无解条件：当k ≥ n或k < ⌈n/2⌉时无解。因为：
- 最少交换次数为n - c，其中c ≤ n/2（因为每个环至少2个元素）。
- 最大交换次数为n - 1（当排列本身是一个大环时）。
构造排列：
- k = n - 1：排列为一个n元环，例如[2, 3, ..., n, 1]。
- k = ⌈n/2⌉：排列为尽可能多的2元环，例如[2, 1, 4, 3, ..., n, n-1]（当n为偶数时）。
- 其他情况：通过调整环的数量和大小来满足c = n - k。

代码实现思路

检查k是否在有效范围内。
根据k的值构造对应的排列：
- 当k = n - 1时，构造一个n元环。
- 当k = ⌈n/2⌉时，构造尽可能多的2元环。
- 其他情况，通过合并或拆分环来调整环的数量。

代码修正

提供的代码中：

当k = (n + 1)/2且n为奇数时，构造了一个特殊情况。
其他情况构造了一个n元环，并通过交换调整环的数量。

需要确保构造的排列满足：

无固定点（a_i ≠ i）。
环的数量c = n - k。

注意事项

确保构造的排列无固定点。
环的数量必须精确控制为c = n - k。
当n为奇数时，可能需要特殊处理最后一个元素。

#include<bits/stdc++.h>
#define ll long long 
#define endl "\n"
using namespace std;
void solve() {int n, k;cin >> n >> k;if (k >= n || k < (n + 1) / 2) {cout << -1 << endl;return;}vector<int>a(n + 1);if(n%2==1&&k==(n+1)/2){for (int i = 1; i <= n; i++) {a[i] = n - i + 1;}swap(a[n / 2], a[n / 2 + 1]);}else {for (int i = 1; i <= n; i++) {a[i] = i + 1;}a[n] = 1;k = n - k - 1;for (int i = 2; i <= n && k > 0; i += 2) {swap(a[i], a[n]);k--;}}for (int i = 1; i <= n; i++) {cout << a[i] << " ";}cout << endl;return;
}
int main(){ios::sync_with_stdio(false);        // 禁用同步std::cin.tie(nullptr),std::cout.tie(nullptr);             // 解除cin与cout绑定int t = 1;//cin >> t;while (t--) {solve();}return 0;
}

查看全文

http://www.dtcms.com/a/420321.html