当前位置：首页 > news >正文

大型语言模型的门控注意力：非线性、稀疏性与无注意力沉没

news 2025/9/29 11:54:31

摘要

https://arxiv.org/pdf/2505.06708
门控机制已被广泛应用，从早期的LSTM（Hochreiter & Schmidhuber, 1997）和Highway Networks（Srivastava et al., 2015）到近期的状态空间模型（Gu & Dao, 2023）、线性注意力（Hua et al., 2022）以及softmax注意力（Lin et al., 2025）。然而，现有文献很少探讨门控的具体效果。在本研究中，我们进行了全面的实验，系统地探究了门控增强的softmax注意力变体。具体而言，我们在一个3.5万亿token的数据集上，对30多种15B规模的混合专家（MoE）模型和1.7B规模的稠密模型进行了全面比较。我们的核心发现是，一个简单的修改——在缩放点积注意力（SDPA）之后应用一个头特定的sigmoid门控——能够持续地提升性能。这种修改还能增强训练稳定性，容忍更大的学习率，并改善模型的扩展性。通过比较各种门控位置和计算变体，我们将这种有效性归因于两个关键因素：(1) 在softmax注意力的低秩映射上引入了非线性；(2) 应用了查询依赖的稀疏门控分数来调制SDPA的输出。值得注意的是，我们发现这种稀疏门控机制能够缓解“注意力沉没”（attention sink）问题，并提升长上下文外推性能。我们也将发布相关的代码和模型，以促进未来的研究。

1 引言

门控机制在神经网络中已得到充分验证。早期的架构，如LSTM（Hochreiter & Schmidhuber, 1997）、Highway Networks（Srivastava et al., 2015）和GRU（Dey & Salem, 2017），率先使用门控来控制跨时间步或跨层的信息流并改善梯度传播。这一原则在现代架构中依然存在。近期的序列建模工作，包括状态空间模型（Gu & Dao, 2023; Dao & Gu, 2024）和注意力机制（Hua et al., 2022; Sun et al., 2023; Qin et al., 2024a; Yang et al., 2024b; Lin et al., 2025），通常会应用门控，经常用于调制token混合组件的输出。尽管其被广泛采用且经验上取得了成功，但门控机制的功能和影响在最初的直觉之外仍缺乏充分探索。理解上的不足阻碍了我们评估门控的真实贡献，尤其是在与其他架构因素混杂的情况下。例如，虽然Switch Heads（Csordas et al., 2024a;b）引入了sigmoid门控来选择前K个注意力头专家，但我们的实验揭示了一个有趣的发现（附录A.1）：即使简化为单个专家，其性能增益依然显著，此时门控仅用于调制值（value）的输出。这强烈表明门控本身提供了重要的内在价值，与路由机制无关。同样，在原生稀疏注意力（NSA）（Yuan et al., 2025）中，尽管展示了整体性能的提升，但并未将其门控机制的贡献与稀疏注意力设计本身的效果区分开来。这些考虑凸显了将门控效果与其他架构组件严格解耦的必要性。

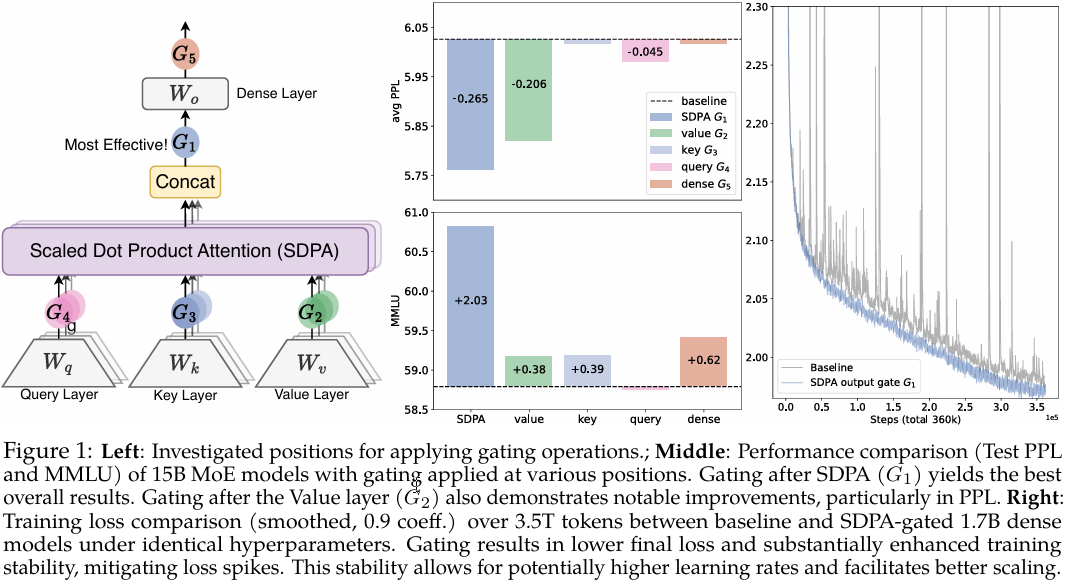
在本研究中，我们探究了标准softmax注意力（Vaswani, 2017）（第2.2节）中的门控机制。具体来说，我们在不同位置引入门控（图1）：查询（G4）、键（G3）和值（G2）投影之后；缩放点积注意力（SDPA）输出之后（G1）；以及最终稠密输出层之后（G5）。我们的探索涵盖了多种门控变体，包括逐元素（elementwise）和逐头（headwise）、头特定（head-specific）和头共享（head-shared），以及加性和乘性形式。我们发现：(i) 在SDPA输出上应用头特定门控（G1）能带来最显著的性能提升（例如，困惑度PPL最多降低0.2，MMLU分数提升2分）；(ii) SDPA输出门控还能提高训练稳定性，几乎消除了损失尖峰，从而允许使用更大的学习率并增强模型的可扩展性。
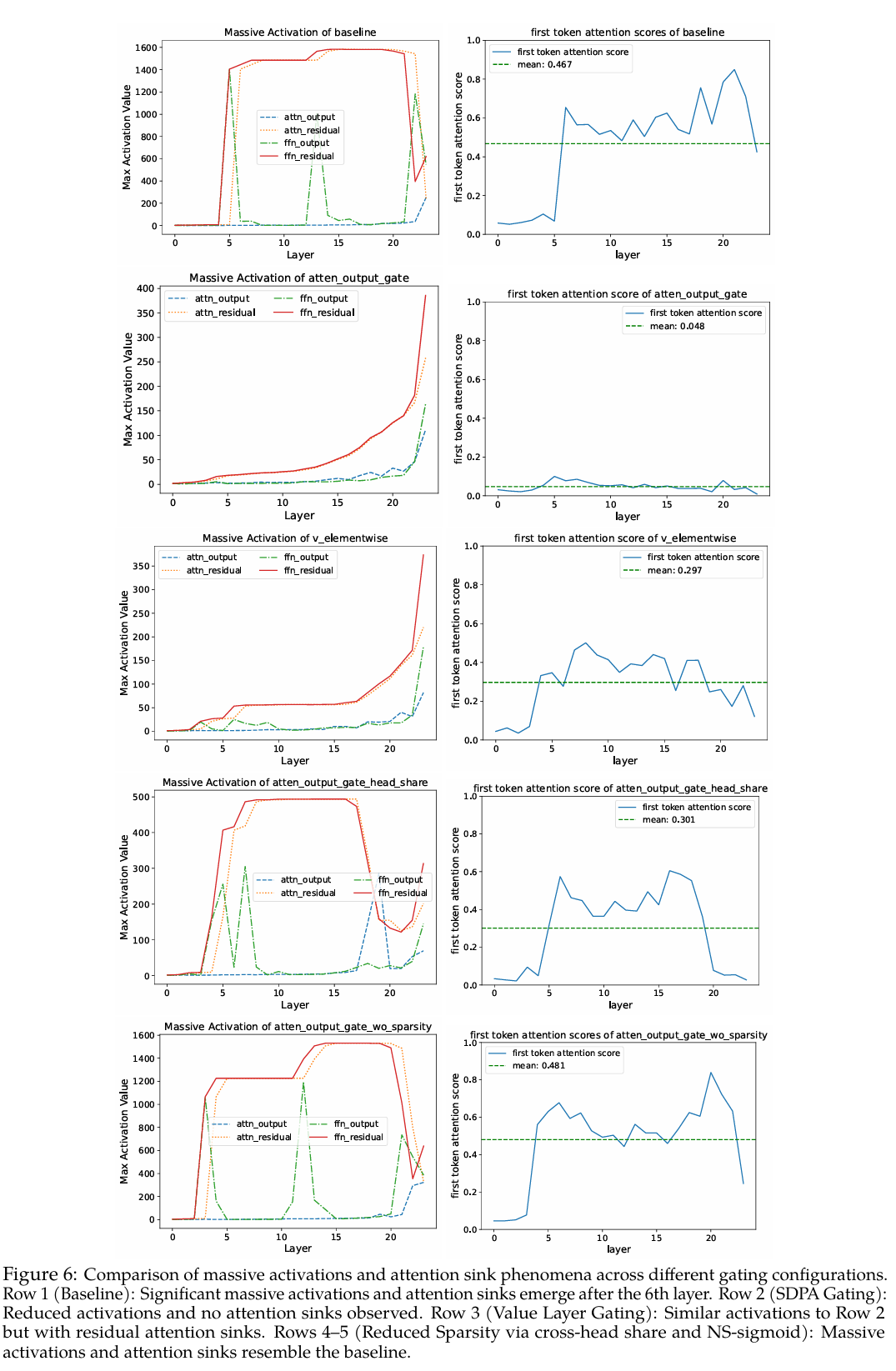
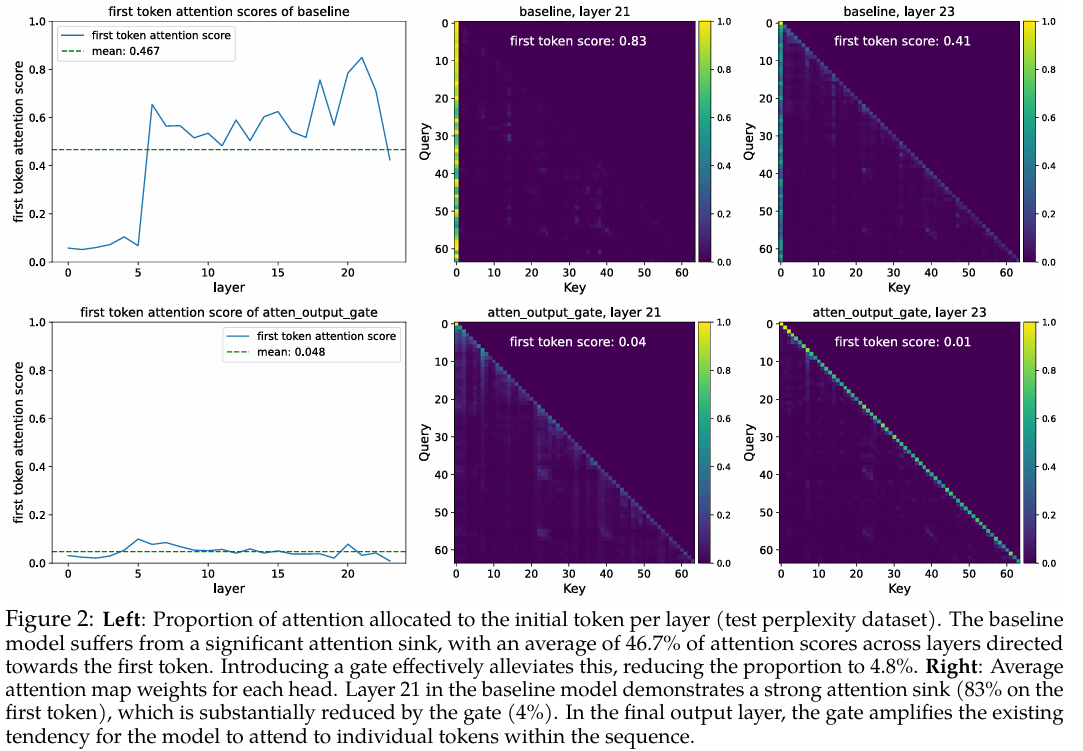
在这里插入图片描述

我们确定了门控有效性的两个主要因素：(i) 非线性。值（ $W_v$ ）和稠密（ $W_o$ ）投影这两个连续的线性层可以被重写为一个低秩线性投影。因此，在 $G_{1}$ 或 $G_{2}$ 位置通过门控引入非线性，可以增强这个低秩线性变换的表达能力（第4.1节）。(ii) 稀疏性。尽管非线性门控变体始终能提升性能，但我们观察到其增益程度各不相同。我们的分析进一步揭示，门控分数的显著稀疏性是另一个关键因素，它为SDPA输出引入了输入依赖的稀疏性（第4.2节）。此外，稀疏门控消除了“注意力沉没”（Xiao et al., 2023）：初始token不成比例地主导了注意力分数（图2，第4.3节）。先前的工作（Xiao et al., 2023; Sun et al., 2024; Gu et al., 2024）将注意力沉没解释为由于非负的softmax归一化导致的冗余注意力累积。通过实验，我们验证了当在SDPA输出处应用查询依赖的稀疏门控时，我们的稠密模型和MoE模型（均在3.5T token上训练）均未出现注意力沉没现象。此外，这些模型在长度泛化方面表现出色，在RULER（Hsieh et al., 2024）基准上获得了超过10分的提升（第4.4节）。
在这里插入图片描述

总之，我们的工作强调了门控在标准注意力层中对模型性能和行为的影响。通过评估各种门控变体，我们揭示了它们引入非线性和稀疏性以及消除注意力沉没的能力。这些发现加深了我们对门控注意力机制的理解。我们将开源我们的无注意力沉没模型，以推动未来的研究。

2 门控注意力层

2.1 预备知识：多头Softmax注意力

给定一个输入 $X∈Rn×dmodelX\in\mathbb{R}^{n\times d_{\mathrm{model}}}$ ，其中 $n$ 是序列长度， $dmodeld_{\mathrm{model}}$ 是模型维度，Transformer的注意力层（Vaswani, 2017）的计算可分为四个阶段。

QKV线性投影：输入 $X$ 通过学习到的权重矩阵 $WQ,WK,WV∈Rdmodel×dkW_{Q},W_{K},W_{V}\in\mathbb{R}^{d_{\mathrm{model}}\times d_{k}}$ 线性变换为查询（queries） $Q$ 、键（keys） $K$ 和值（values） $V$ ，并且 $Q,K,V∈Rn×dkQ,K,V\in\mathbb{R}^{n\times d_{k}}$ ：
$W_{Q},\quad K=X W_{K},\quad V=X W_{V}.$

缩放点积注意力（SDPA）：计算查询和键之间的注意力分数，然后进行softmax归一化。输出是值的加权和：
$Attention⁡(Q,K,V)=softmax⁡(QKTdk)V,\operatorname{Attention}\bigl(Q,K,V\bigr)=\operatorname{softmax}\left({\frac{Q K^{T}}{\sqrt{d_{k}}}}\right)V,$
其中 $QKTdk∈Rn×n{\frac{Q K^{T}}{\sqrt{d_{k}}}\in\mathbb{R}^{n\times n}}$ 代表缩放的点积相似度矩阵， $softmax⁡(⋅)\operatorname{softmax}(\cdot)$ 确保注意力权重非负且每行之和为1。

多头拼接：在多头注意力中，上述过程在 $h$ 个头上并行重复，每个头都有其投影矩阵 $W_{q}^{i},W_{k}^{i},W_{v}^{i}$ 。所有头的输出被拼接起来：
$MultiHead⁡(Q,K,V)=Concat⁡(head⁡1,…,head⁡h),\operatorname{MultiHead}\bigl(Q,K,V\bigr)=\operatorname{Concat}(\operatorname{head}_{1},\ldots,\operatorname{head}_{h}),$
其中 $head⁡i=Attention⁡(QWQi,KWKi,VWVi)\operatorname{head}_{i} = \operatorname{Attention} \left(Q W_{Q}^{i},K W_{K}^{i},V W_{V}^{i}\right)$ 。

最终输出层：拼接后的SDPA输出通过一个输出层 $Wo∈Rhdk×dmodelW_{o}\in\mathbb{R}^{h d_{k}\times d_{\mathrm{model}}}$ ：
$O=MultiHead(Q,K,V)Wo.O=\mathrm{MultiHead}\big(Q,K,V\big)W_{o}.$

2.2 用门控机制增强注意力层

门控机制的形式化定义为：
$Y′=g(Y,X,Wθ,σ)=Y⊙σ(XWθ),Y^{\prime}=g\big(Y,X,W_{\theta},\sigma\big)=Y\odot\sigma\big(X W_{\theta}\big),$
其中 $WθW_{\theta}$ 是门控的可学习参数， $σ\sigma$ 是一个激活函数（例如，sigmoid），而 $Y′Y^{\prime}$ 是门控后的输出。门控分数 $σ(XWθ)\sigma(X W_{\theta})$ 有效地充当了一个动态滤波器，通过选择性地保留或擦除 $Y$ 的特征来控制信息流。

在本研究中，我们全面探究了注意力层内门控机制的多种变体。我们的探索聚焦于五个关键方面：
(1) 位置。我们研究了在不同位置应用门控的效果，如图1（左）所示：(a) 在 $Q, K, V$ 投影之后（公式1），对应图1（左）中的位置 $G_{2},G_{3},G_{4}$ ；(b) 在SDPA（公式3）输出之后（ $G1ˉ\bar{G_{1}}$ ）；© 在最终拼接的多头注意力输出之后（公式4, $G_{5}$ ）。
(2) 粒度。我们考虑了门控分数的两个粒度级别：(a) 逐头（Headwise）：单个标量门控分数调制整个注意力头的输出。(b) 逐元素（Elementwise）：门控分数是与 $Y$ 维度相同的向量，能够实现细粒度的、逐维度的调制。
(3) 头特定或共享。鉴于注意力的多头特性，我们进一步考虑：(a) 头特定（Head-Specific）：每个注意力头都有其特定的门控分数，从而实现对每个头的独立调制。(b) 头共享（Head-Shared）： $WθW_{\theta}$ 和门控分数在所有头之间共享。
(4) 乘性或加性。对于将门控分数应用于 $Y$ ，我们考虑：(a) 乘性门控（Multiplicative Gating）：门控输出 $Y′Y^{\prime}$ 计算为： $Y′=Y⊙σ(XWθ)Y^{\prime} = Y \odot \sigma(X W_{\theta})$ 。(b) 加性门控（Additive Gating）： $Y′=Y+σ(XWθ)Y^{\prime} = Y + \sigma(X W_{\theta})$ 。
(5) 激活函数。我们主要考虑两种常见的激活函数：SiLU（Shazeer, 2020）和sigmoid。由于SiLU的输出范围无界，我们仅在加性门控中使用它；而sigmoid的输出范围在 $[0, 1]$ 之间。

除非另有说明，我们采用头特定、乘性门控，并使用sigmoid激活函数 ( $σ(x)=11+e−x\sigma(x)={\frac{1}{1+e^{-x}}}$ )。

在这里插入图片描述

3 实验

3.1 实验设置

模型架构与训练设置：我们在混合专家（MoE）模型（总计15B参数，激活2.54B，记为15A2B）和稠密模型（总计1.7B参数）上进行实验。15A2B MoE模型采用128个专家，top-8 softmax门控、细粒度专家（Dai et al., 2024）、全局批次LBL（Qiu et al., 2025）和z-loss（Zoph et al., 2022）。我们在注意力部分采用分组查询注意力（GQA）（Ainslie et al., 2023）。我们在一个3.5T高质量token数据集的子集上训练模型，内容涵盖多语言、数学和通用知识。上下文序列长度设为4096。学习率和批次大小（bsz）等更详细的配置将在各部分中介绍。其他超参数遵循AdamW优化器的默认值。由于门控引入的参数和计算量很小，因此门控带来的实际延迟（wall-time latency）不到2%。

评估：我们在流行的基准上测试少样本（few-shot）结果，包括用于英语的Hellaswag（Zellers et al., 2019）、用于通用知识的MMLU（Hendrycks et al., 2020）、用于数学推理的GSM8k（Cobbe et al., 2021）、用于代码的HumanEval（Chen et al., 2021）、以及用于中文能力的C-eval（Huang et al., 2024）和CMMLU（Li et al., 2023）。我们还报告了在多样化的保留测试集（held-out test sets）上的语言建模困惑度（PPL），这些测试集涵盖英语、中文、代码、数学、法律和文学等领域。

3.2 主要结果

3.2.1 MoE模型的门控注意力

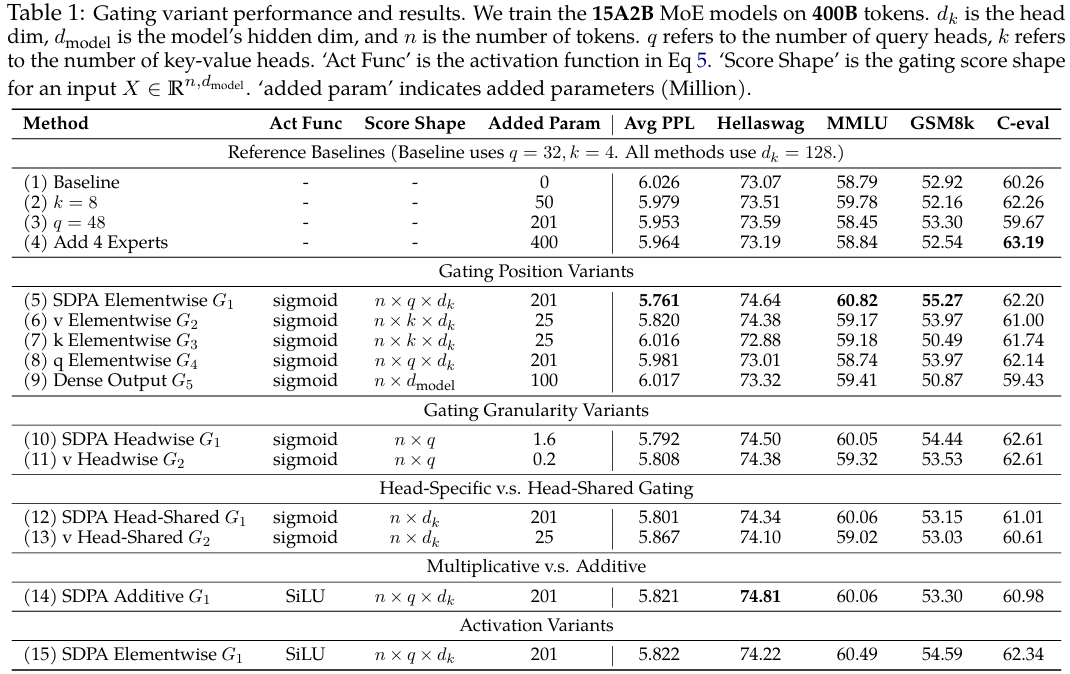
我们首先在训练高效的MoE-15A2B模型上比较不同门控注意力层的结果。所有模型均使用一个调度器，在1k步内将学习率（LR）从0线性预热到最大值2e-3，然后使用余弦衰减到3e-5。我们使用1024的全局批次大小（bsz），共进行100k次优化步。结果汇总在表1中。为了提供公平的比较，我们用参数扩展方法补充了基础的MoE模型（第1行），包括增加键-值头的数量（第2行）、增加查询头的数量（第3行）以及同时增加总专家数和激活专家数（第4行）。这些方法引入的参数量与门控机制相当或更多。

从表1中，我们观察到：
(i) SDPA和值输出门控是有效的。在SDPA（ $G_1$ ）或值映射（ $G_2$ ）的输出处插入门控是最有效的，相比其他变体，能获得更低的PPL和更好的整体基准性能。我们将在第4.2节进一步探究为何在这两个位置进行门控是有效的。
(ii) 头特定门控很重要。在 $G_1$ 和 $G_2$ 位置应用逐头门控为MoE-15A2B模型引入的额外参数非常少（少于2M），但仍能带来显著的改进（第10和11行）。当在不同注意力头之间共享门控分数时（我们对查询头维度 $q$ 取平均，从原始的 $n×q×dkn\times q\times d_k$ 得到 $n×dkn\times d_k$ 的分数），基准测试的改进幅度小于逐头门控（第12行 vs. 第10行，第13行 vs. 第11行）。这凸显了为不同注意力头应用不同门控分数的重要性。
(iii) 乘性门控更优。加性SDPA输出门控的表现不如乘性门控，尽管它比基线有所改进。
(iv) Sigmoid激活函数更好。在最有效的门控配置（第5行）中，将激活函数替换为SiLU（第15行）会导致改进幅度减小。

总的来说，在值层（ $G_2$ ）和SDPA输出（ $G_1$ ）处添加门控可使PPL降低超过0.2，优于各种参数扩展的基线。然而， $G_1$ 位置的门控在PPL和基准测试结果上表现更好。只要不同的头能接收到不同的门控分数，门控的粒度和激活函数的选择影响就相对较小。我们将在分析部分（第4.2节）进一步分析这些观察结果背后的原因。

3.2.2 稠密模型的门控注意力

我们还参照（Yang et al., 2024a）在稠密模型上进行实验，以验证SDPA输出的sigmoid门控。使用门控时，我们会减小FFN的宽度以保持参数量不变。大多数实验使用针对基线优化的超参数。例如，对于在400B token上训练的1.7B模型，我们使用4e-3的最大LR和1024的bsz。对于在3.5T token上训练的模型，我们将最大LR提高到4.5e-3，bsz提高到2048。先前的工作已表明，虽然增加网络深度、使用大学习率和大批次大小可以显著提升模型性能（McCandlish et al., 2018; Wang et al., 2022; D’Angelo et al., 2024）和分布式训练效率，但它们常常会引入训练不稳定性（Wang et al., 2022; Zeng et al., 2022; Takase et al., 2023）。我们观察到，应用门控机制能显著减少训练过程中的损失尖峰（loss spikes）（Chowdhery et al., 2023; Takase et al., 2023），这表明门控在增强训练稳定性方面具有重要作用。受此发现的启发，我们引入了另一种实验设置，其特点是层数更多、最大学习率更高、批次大小更大，以进一步探究门控的稳定效果。
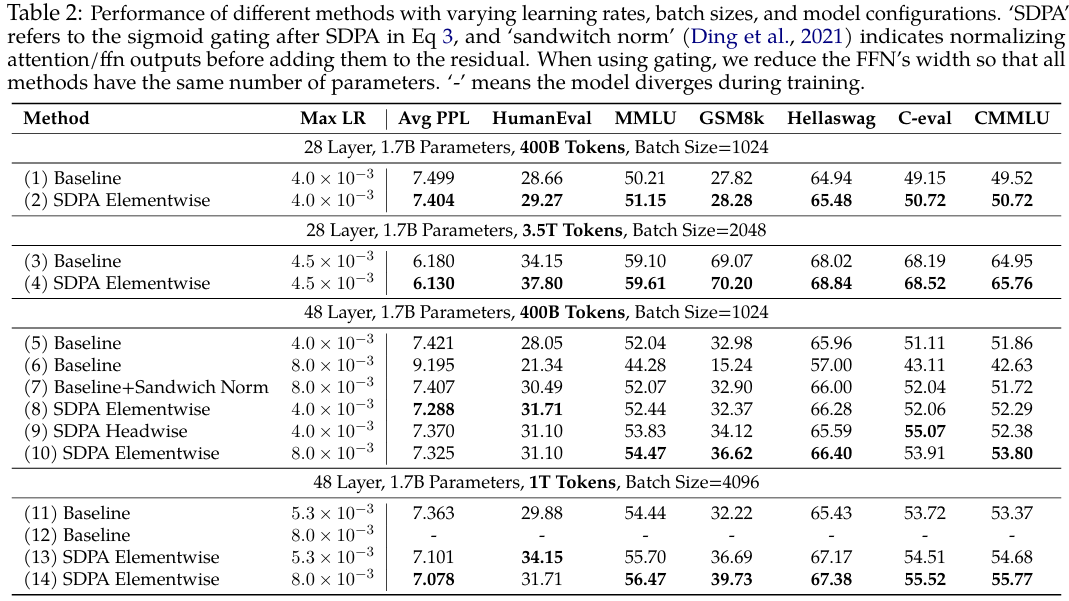
在这里插入图片描述

表2显示：
(i) 门控在各种设置下均有效。在不同的模型配置（第1行 vs. 第2行，第5行 vs. 第8行）、训练数据（第3行 vs. 第4行）和超参数（第11行 vs. 第13行）下，应用SDPA输出门控始终能带来收益。
(ii) 门控提升了稳定性并促进了扩展。在3.5T token设置下，门控提高了训练稳定性，大幅减少了损失尖峰（图1，右）。当增加最大LR时，基线模型会遇到收敛问题（第6行，第12行）。虽然添加sandwich norm（Ding et al., 2021）可以恢复收敛，但改进微乎其微。相比之下，在带门控的模型中增加最大LR则能带来明显的性能提升。

总之，我们将SDPA逐元素门控确定为增强注意力机制的最有效方法。将此方法应用于稠密Transformer进一步证明，该门控能够支持使用更大的批次大小和学习率进行稳定训练，从而获得更好的性能。

4 分析：非线性、稀疏性与无注意力沉没

在本节中，我们进行了一系列实验，以探究为何如此简单的门控机制能在性能和训练稳定性上带来显著提升。根据我们的分析，主要结论如下：(1) 增强非线性的门控操作始终能带来性能提升（第4.1节）；(2) 最有效的SDPA逐元素 $G_1$ 门控为SDPA输出引入了强烈的输入依赖稀疏性（第4.2节），这有助于消除“注意力沉没”（attention sink）现象。

4.1 非线性提升了注意力中低秩映射的表达能力

受先前在SDPA输出上使用分组归一化的工作（Sun et al., 2023; Ye et al., 2024）启发，在第3.2.1节的相同设置下，我们在拼接前对每个注意力头的输出独立应用RMSNorm（Zhang & Sennrich, 2019）。如表3第5行所示，引入几乎不增加额外参数的RMSNorm也能显著降低PPL。

在多头注意力中，第 $i$ 个token在第 $k$ 个头上的输出可以表示为：
$oik=(∑j=0iSijk⋅XjWVk)WOk=∑j=0iSijk⋅Xj(WVkWOk),o_{i}^{k}=(\sum_{j=0}^{i}S_{i j}^{k}\cdot X_{j}W_{V}^{k})W_{O}^{k}=\sum_{j=0}^{i}S_{i j}^{k}\cdot X_{j}(W_{V}^{k}W_{O}^{k}),$
其中 $W_{O}^{k}$ 是输出层 $W_{O}$ 中对应于第 $k$ 个头的参数。这里， $S_{i j}^{k}$ 表示第 $k$ 个头中第 $i$ 个token对第 $j$ 个token的注意力分数， $X_{j}$ 是第 $j$ 个token的注意力输入， $X_{j}W_{V}^{k}$ 代表第 $j$ 个token在第 $k$ 个头中的值输出。从公式6可以看出，我们可以将 $W_{V}^{k}W_{O}^{k}$ 合并为一个应用于所有 $X_{j}$ 的低秩线性映射，因为 $dk<dmodeld_{k}<d_{\mathrm{model}}$ 。在GQA中， $W_{V}$ 在同一组内的头之间共享，这进一步降低了表达能力。

鉴于在两个线性映射之间添加非线性可以提升其表达能力（Montufar et al., 2014），我们有两种修改方式来缓解低秩问题：
$oik=(∑j=0iSijk⋅Non-Linearity-Map(XjWVk))WOk,oik=Non-Linearity-Map(∑j=0iSijk⋅XjWVk)WOk.\begin{aligned}&o_{i}^{k}=\left(\sum_{j=0}^{i}S_{ij}^{k}\cdot \text{Non-Linearity-Map}\big(X_{j}W_{V}^{k}\big)\right)W_{O}^{k},\\&\quad o_{i}^{k}=\text{Non-Linearity-Map}\left(\sum_{j=0}^{i}S_{ij}^{k}\cdot X_{j}W_{V}^{k}\right)W_{O}^{k}.\\ \end{aligned}$
值得注意的是，在 $G_2$ 位置添加门控（表3第3行）对应于第一种修改（公式7），而在 $G_1$ 位置添加门控（第4行）或分组归一化（第5行）则对应于第二种（公式8）。这也解释了为什么在 $W_O$ 之后的 $G_5$ 位置添加门控或归一化没有效果（表1第9行）——因为它没有解决 $W_V$ 和 $W_O$ 之间缺乏非线性的问题。

对于 $G_1$ 位置的加性门控，门控的输出会经过SiLU（表3第4行），这也引入了一些非线性，这解释了观察到的性能提升，尽管其幅度小于乘性门控。基于这些见解，我们进行了两个额外的实验：(i) 仅在 $G_1$ 位置添加SiLU，而不引入额外参数（表3第6行）。请注意，这种简单修改也能带来适度的PPL降低，但大多数基准分数保持不变。(ii) 从加性门控中移除SiLU，使得 $X_j$ 经过门控后的输出直接在 $G_1$ 位置相加（表3第7行）。这进一步削弱了加性门控的收益。
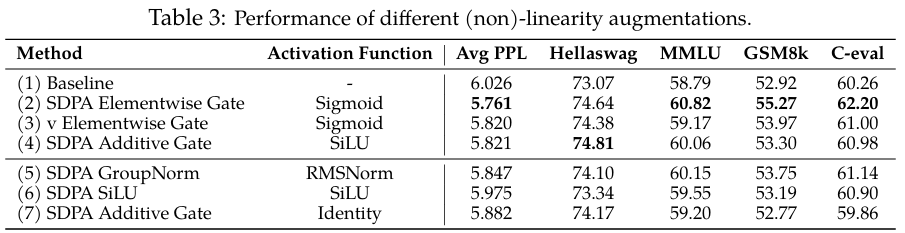
在这里插入图片描述

总之，有效门控变体带来的性能提升很可能归因于在 $W_V$ 和 $W_O$ 之间引入了非线性。虽然在 $G_1$ 和 $G_2$ 位置应用门控都能引入这种非线性，但它们带来的性能提升却不同。这一观察到的差异促使我们进一步分析在这两个位置进行门控的影响。
在这里插入图片描述

4.2 门控引入了输入依赖的稀疏性

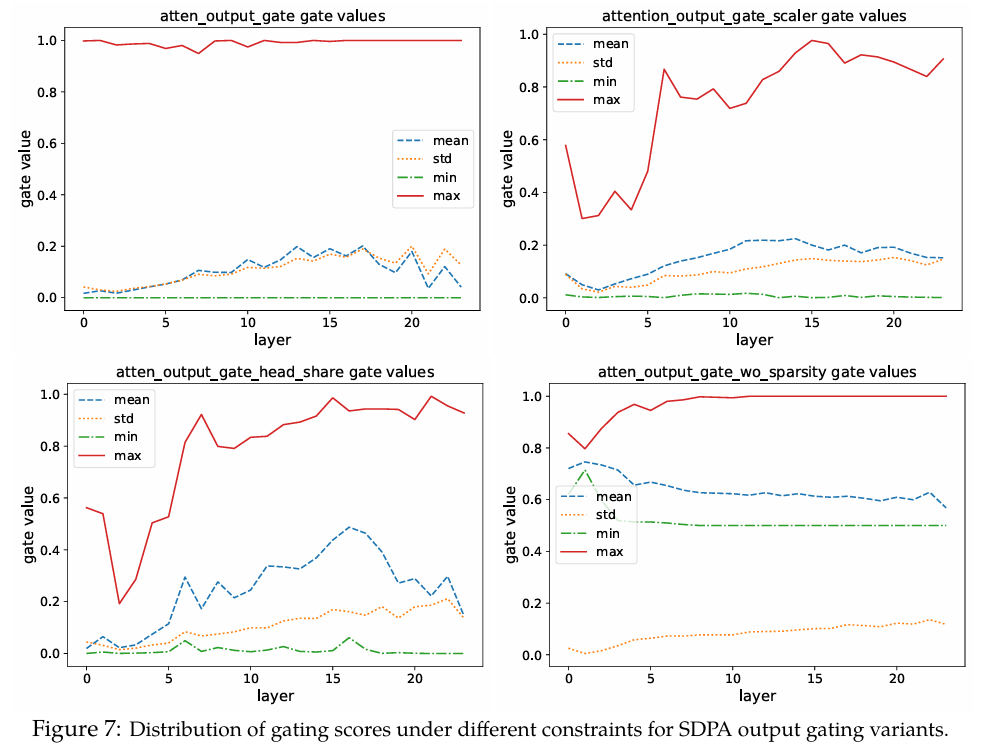
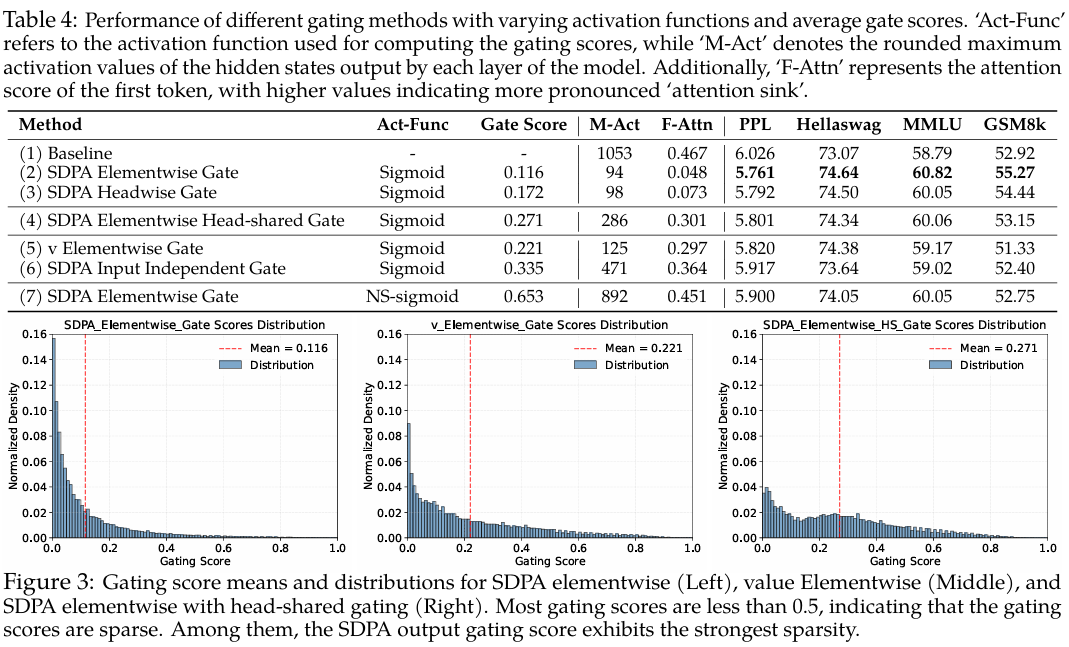
我们分析了在值（ $G_2$ ）和SDPA输出（ $G_1$ ）位置应用门控的模型在测试语言建模数据上的门控分数（表1，“Gate Score”列）。所有层的平均门控分数如表4所示，分数分布如图3所示（逐层分数见附录A.2）。主要观察结果包括：

(i) 有效的门控分数是稀疏的。SDPA输出门控（逐元素/逐头）表现出最低的平均门控分数。此外，SDPA输出门控分数分布显示出在0附近高度集中，表明其具有显著的稀疏性，这与其优越的性能一致。
(ii) 头特定的稀疏性很重要。强制在注意力头之间共享门控分数会提高整体门控分数并削弱性能增益。观察(i)和(ii)强调了头特定门控的重要性，这与先前的研究一致，即各个注意力头捕获输入的不同方面（Voita et al., 2019; Wang et al., 2021; Olsson et al., 2022; Wang et al., 2023）。
(iii) 查询依赖性很重要。值门控（ $G_2$ ）的分数高于SDPA输出门控（ $G1~\widetilde{G_1}$ ），且性能更差。这表明，当门控分数是查询依赖的，而非由键和值决定时，其稀疏性更为有效。具体来说，SDPA输出门控分数源自与当前查询对应的隐藏状态（例如，公式8中的Non-Linearity-Map依赖于 $X_i$ ），而值门控分数则源自与过去键和值相关的隐藏状态（例如，公式7中的Non-Linearity-Map依赖于每个 $X_j$ ）。这意味着门控分数的稀疏性可能会过滤掉与查询无关的上下文信息。为了进一步验证查询依赖性的重要性，我们通过将可学习参数（ $\times d_k$ ）零初始化、应用sigmoid函数并将其与SDPA输出相乘，引入了输入无关的门控。如第(6)行所示，输入无关的门控优于基线，这可能是因为引入了非线性。此外，较高的门控分数也印证了有效的稀疏性应该是输入依赖的。
(iv) 稀疏性越低效果越差。为了进一步验证门控分数稀疏性的重要性，我们从门控公式中减少了稀疏性。具体来说，我们将sigmoid函数替换为一个修改后的非稀疏（NS）版本：
$NS-sigmoid⁡(x)=0.5+0.5⋅sigmoid⁡(x),\operatorname{NS\text{-}sigmoid}\bigl(x\bigr)=0.5+0.5\cdot\operatorname{sigmoid}\bigl(x\bigr),$
这将门控分数约束在 $[0.5, 1.0]$ 之间。这确保了引入非线性的同时去除了门控分数的稀疏性。如表4第(7)行所示，NS-sigmoid门控的收益不如SDPA输出sigmoid门控。在附录A.2中，我们更详细地讨论了稀疏门控分数如何影响SDPA隐藏状态的稀疏性（低于阈值的值的比例）。我们将在下一节讨论不同稀疏性水平对模型行为的影响，包括减少“注意力沉没”。

4.3 SDPA输出门控减少了注意力沉没

基于门控以输入依赖的方式为SDPA输出引入稀疏性的观察，我们假设这种机制可以过滤掉与当前查询token无关的上下文，从而缓解注意力沉没（Xiao et al., 2023; Sun et al., 2024）。为了验证这一点，我们分析了注意力分数（在所有头上取平均）的分布以及分配给第一个token的注意力分数比例（图2，表4，“F-Attn”列）。受关于隐藏状态中大规模激活与注意力沉没的讨论（Sun et al., 2024）启发，我们还计算了各层最大隐藏状态激活的平均值，如表4的“M-Act”列所示。更详细的逐层结果见附录A.3。

我们可以观察到：
(i) 在SDPA输出（ $G_1$ ）处进行逐头和逐元素的查询依赖sigmoid门控，大幅减少了分配给第一个token的注意力分数，并降低了大规模激活。
(ii) 强制在头之间共享门控分数或仅在值投影后（ $G_2$ ）应用门控，虽能降低大规模激活，但并未减少对第一个token的注意力分数。这再次强调了头特定门控的重要性，并表明大规模激活并非注意力沉没的先决条件。
(iii) 降低门控的输入依赖性（第6行）或使用NS-sigmoid来降低稀疏性（第7行），都会加剧大规模激活和注意力沉没。

综合来看，这些观察结果表明，对SDPA输出进行输入依赖、头特定的门控引入了显著的稀疏性，从而缓解了注意力沉没。此外，SDPA输出的稀疏性减少了模型内部的大规模激活，稀疏性越高，激活值越小。这或许可以解释门控带来的训练稳定性提升：通过减少大规模激活，模型在BF16训练期间对数值误差的敏感性降低（Budzinskiy et al., 2025）。我们还观察到，大规模激活主要源自早期层（例如第5层），其中FFN输出了很大的值，这与（Yona et al., 2025）的研究一致。一旦这些激活被添加到残差流中，就会通过预归一化（pre-norm）机制传播到后续层。这与sandwich归一化（Ding et al., 2021）在提升训练稳定性方面的有效性相吻合（表2，第7行）：对FFN输出应用LayerNorm可以防止这些大激活值进入残差流。

4.4 SDPA输出门控促进了上下文长度扩展

基于无注意力沉没的模式，我们在长上下文设置下评估了SDPA门控的效果。具体来说，我们扩展了在3.5T token上训练的模型的上下文长度。我们将RoPE（Su et al., 2024）的基底（base）从10k增加到1M，并在序列长度为32k的数据上继续训练了额外的80B token。这使我们得到了上下文长度为32k的模型。随后，我们使用YaRN（Peng et al., 2023）将上下文长度扩展到128k。我们在RULER基准（Hsieh et al., 2024）上评估模型，结果汇总在表5中。我们观察到以下几点：
(i) 在32k设置下，带门控的模型略优于基线。这表明在训练长度内，注意力沉没现象可能不会损害模型的长上下文性能。
(ii) 当使用YaRN将上下文长度扩展到128k时，基线模型和带门控模型在原始的32k范围内都出现了性能下降。这一观察结果与先前通过修改RoPE来扩展上下文长度的工作一致（Chen et al., 2023; Peng et al., 2023; Dong et al., 2025）。尽管带门控模型的下降幅度较小。
(iii) 在64k和128k的上下文长度下，带门控注意力的模型显著优于基线。

从这些观察中，我们推测添加门控有助于模型适应上下文长度的扩展。一种可能的解释是，基线模型依赖注意力沉没来调整注意力分数的分布。Dong等人（2025）基于注意力和隐藏状态分布推导了改变RoPE的效果。当应用YaRN等技术修改RoPE基底时，注意力沉没模式可能难以在无需训练的情况下进行适应，从而导致性能显著下降。相比之下，带门控的模型主要依靠输入依赖的门控分数来控制信息流，使其对这类变化更具鲁棒性。这项工作是2025年阿里Qwen团队的成果，系统性地探讨了门控机制在标准softmax注意力中的作用，揭示其对模型性能、训练稳定性和注意力动态具有显著影响。

5 相关工作

5.1 神经网络中的门控

门控机制已被广泛应用于神经网络。早期的工作，如LSTM（Hochreiter & Schmidhuber, 1997）和GRU（Dey & Salem, 2017），引入了门控来调节跨时间步的信息流，通过选择性地保留或丢弃信息来解决梯度消失/爆炸问题。Highway Networks（Srivastava et al., 2015）将这一概念扩展到前馈网络，使得非常深的架构能够成功训练。SwiGLU（Shazeer, 2020）将门控机制引入到Transformer的FFN层中，增强了其表达能力，并成为许多开源大语言模型（LLM）的标准组件（Grattafiori et al., 2024; Yang et al., 2024a）。

一些关于状态空间模型（Gu & Dao, 2023; Dao & Gu, 2024）和线性注意力的工作，如FLASH（Hua et al., 2022）、RetNet（Sun et al., 2023）、Lightning Attention（Qin et al., 2024a;b; Li et al., 2025）和Gated Delta Networks（Yang et al., 2024b），也包含了门控模块来控制token混合模块的信息。Forgetting Transformer（Lin et al., 2025）将门控机制应用于softmax注意力的输出，并观察到显著的性能提升。尽管这些工作证明了门控的有效性，但对于其精确机制及其有效性的原因仍缺乏全面的理解。这有助于我们更广泛地认识到门控在RNN之外的重要性，并促进设计出能更好利用门控独特优势的模型。例如，Switch Heads（Csordas et al., 2024b;a）、NSA（Yuan et al., 2025）和MoSA（Piekos et al., 2025）都使用基于sigmoid的门控（Csordas et al., 2023）进行选择，进一步研究以分离出门控的具体贡献可能会提供宝贵的见解。与在标准Transformer中采用类似门控机制的基线进行比较，可以更精细地评估其提出的门控选择机制的有效性。与我们工作最相关的是Quantizable Transformers（Bondarenko et al., 2023），该工作也发现，在softmax注意力中应用门控可以缓解编码器模型（如BERT和ViT）中注意力过度集中和隐藏状态中的异常值问题。虽然该工作主要利用门控来消除异常值以进行模型量化，但我们对各种门控变体进行了详细分析，揭示了其通过增强非线性和稀疏性以及提高训练稳定性所带来的好处。基于这些见解，我们对门控注意力模型进行了扩展，展示了门控的广泛适用性和影响力。

5.2 注意力沉没

Xiao等人（2023）正式定义了“注意力沉没”（attention sink）现象，即特定token获得了很大的注意力分数。同样，Darcet等人（2023）发现在视觉Transformer中，一些冗余的token充当“寄存器”来存储注意力分数。后来，Sun等人（2024）表明，与大规模激活值相关的token也会被分配过多的注意力分数。然而，我们的工作揭示，在值投影的输出处应用门控可以消除大规模激活，但注意力沉没现象依然存在，这表明大规模激活并非注意力沉没的必要条件。同样，Gu等人（2024）将注意力沉没描述为存储冗余注意力分数的非信息性“键偏置”（key biases），并认为softmax固有的归一化依赖性驱动了这种行为。一些尝试修改softmax注意力的实验，例如用非归一化的sigmoid注意力替换softmax（Ramapuram et al., 2024; Gu et al., 2024）、在softmax注意力中添加注意力陷阱（Bondarenko et al., 2023）以及修改softmax的计算（Zuhri et al., 2025）和分母（Miller, 2023），在缓解注意力沉没方面显示出潜力。我们的工作证明，在SDPA之后应用稀疏门控可以在稠密（1B参数）和MoE（15B参数）模型中消除注意力沉没，即使这些模型是在3.5T token上训练的。此外，我们还揭示了消除注意力沉没对上下文长度扩展的潜在益处。

6 结论

本工作系统地探究了门控机制在标准softmax注意力中的作用，揭示了其对性能、训练稳定性和注意力动态的显著影响。通过对在最多3.5T token上训练的30多种15B MoE和1.7B稠密模型进行广泛的实验比较，我们证明了在缩放点积注意力之后应用sigmoid门控能带来最显著的改进。这种简单机制增强了非线性，引入了输入依赖的稀疏性，并消除了“注意力沉没”等低效现象。此外，门控促进了上下文长度的扩展，使模型能够在无需重新训练的情况下有效地泛化到更长的序列。我们还发布了首批无注意力沉没的模型。我们相信，这些实证验证将为构建下一代先进基础模型铺平道路。

局限性

我们的工作主要通过一系列消融研究来分析注意力门控的原因和影响。然而，我们承认存在一些局限性。非线性对注意力动态和整体训练过程的更广泛影响仍有待探索。尽管我们观察到消除注意力沉没能改善长上下文扩展场景下的性能，但我们并未提供一个严格的理论解释来说明注意力沉没如何影响模型对更长序列的泛化能力。

附录A：补充实验

A.1 Switch Head基线

在本节中，我们展示了与Switch Heads相关的详细实验。Switch Head论文表明，在注意力中引入稀疏激活——即每个token通过可学习的sigmoid路由从一组键/值/输出专家池中选择top-k个专家——可以使模型获得与基线相当的结果。这表明，在Switch Head框架内，专家参数和激活参数都是有益的，在相同的总参数预算下，越多越好。
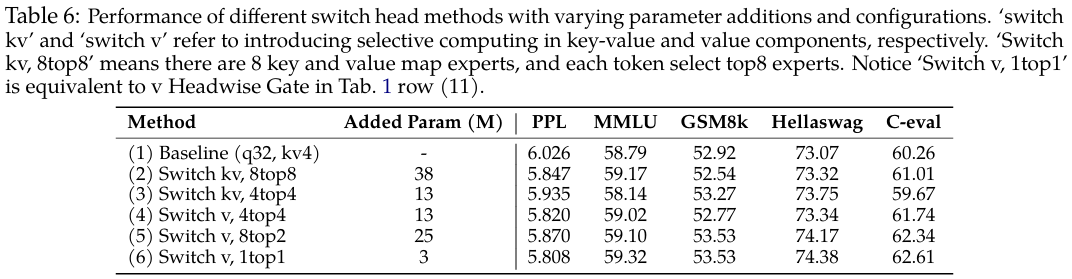
在这里插入图片描述

查看表6中的结果，我们观察到一个有趣的趋势：虽然增加激活的kv专家数量（在相同的专家参数设置下）似乎能带来一些PPL的改进（第4行 vs. 第5行），但在整体基准性能上的收益却不那么明显。值得注意的是，基准分数和PPL的最佳结果是由“Switch v 1top1”（第6行）实现的，如前所述，这类似于直接在值层的输出上应用sigmoid门控。这些发现提出了一个关于这些实验中观察到的性能改进主要驱动因素的有趣问题。它表明门控本身的引入在此方法的有效性中扮演了重要角色。

A.2 关于稀疏门控分数的更多讨论

在本节中，我们分析了门控分数稀疏性对注意力输出的影响。首先，我们检查了对隐藏状态应用门控前后SDPA输出的平均值。具体来说，我们计算了每层在 $G_1$ 位置门控前后 $Y$ 和 $Y^{'}$ 的平均绝对值，如图4所示。我们还包含了无门控基线的结果以供比较。结果表明：(1) 门控后，隐藏状态的平均值从0.71下降到0.05，这与普遍较小的门控分数相对应；(2) 门控后的隐藏状态与基线非常相似，这表明门控可能起到了与注意力沉没类似的作用，即过滤掉无关信息。
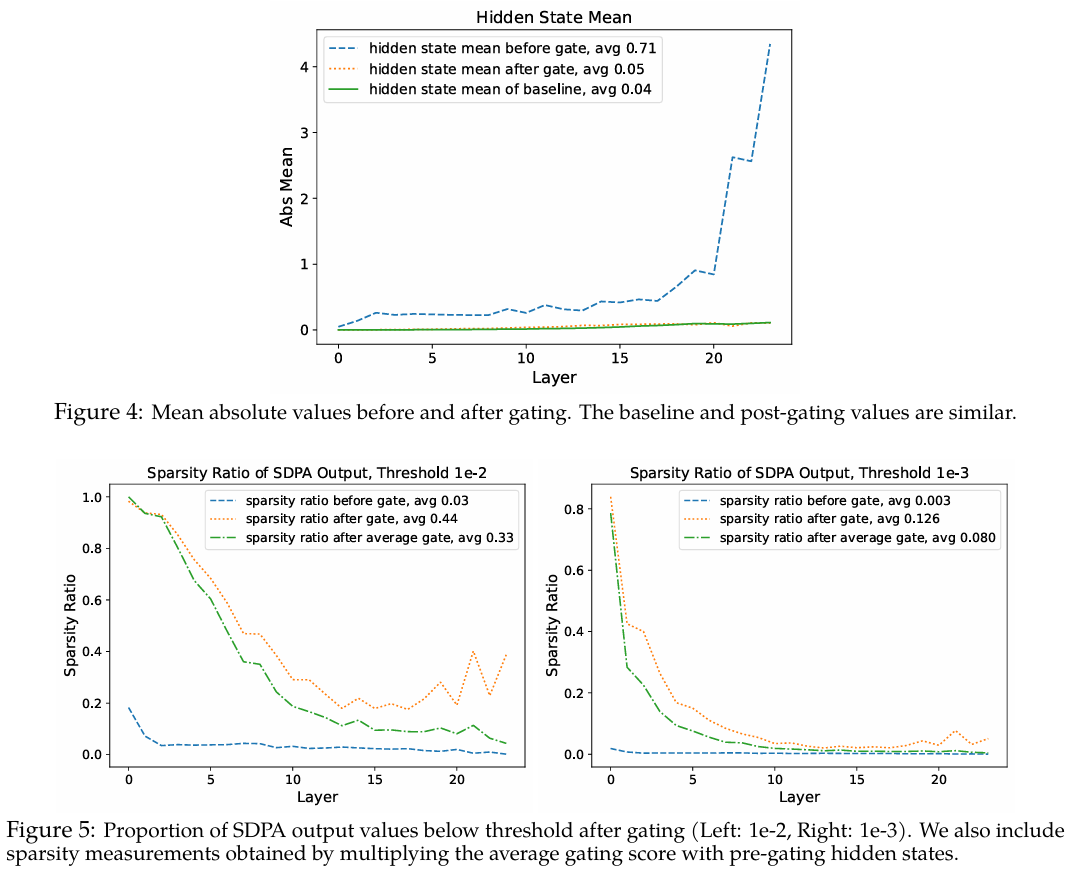
在这里插入图片描述

我们进一步分析了门控前后隐藏状态低于特定阈值的比例，如图5所示。结果揭示：(1) 门控后，不同阈值下的隐藏状态稀疏性显著增加。由于平均门控分数已经很小，将隐藏状态乘以一个小数自然会将一些值推到阈值以下。因此，(2) 我们进一步将门控前的隐藏状态乘以平均门控分数，观察到稀疏性的增加小于原始门控。这表明稀疏的门控分数增强了隐藏状态的稀疏性。

A.3 逐层的大规模激活与注意力沉没

在本节中，我们比较并分析了模型内部大规模激活和注意力沉没（第一个token的注意力分数）的存在情况。从结果中，我们观察到以下几点：

对于基线（第1行），第6层FFN的输出包含大规模激活，这些激活随后被添加到残差流中，导致后续层的残差中持续存在大激活。相应地，从第6层开始出现了显著的注意力沉没现象。在SDPA输出处应用门控后（第2行），网络中较早层的输出总体上仍然相对较小，大规模激活随着层数的增加而逐渐增长。值得注意的是，在网络的任何一层都没有观察到明显的注意力沉没现象。

当仅在值层应用门控时（第3行），模型表现出与第2行类似的大规模激活。然而，一定程度的注意力沉没现象仍然存在。这表明大规模激活并非注意力沉没出现的必要条件。当强制在不同头之间共享门控分数（第4行）或修改门控的激活函数以抑制稀疏性（第5行）时，门控引入的稀疏性会降低。在这些情况下，大规模激活和注意力沉没都与基线中观察到的情况相当。

这些观察结果表明，在注意力机制中引入足够的稀疏性可能有助于缓解大规模激活的发生。然而，需要进一步的研究来充分理解稀疏性、大规模激活和注意力沉没之间的相互作用，特别是在扩展到更深、更大模型的背景下。

A.4 更多的逐层门控分数

在本节中，我们在使用SDPA输出门控作为基线（第1行，逐元素/逐头）的情况下，分析了在两种额外约束下门控分数的分布：(1) 强制在不同头之间使用相同的门控分数（第2行，左）；(2) 限制门控分数的最小值（第2行，右）。当强制在不同头之间共享门控分数时，大多数层的门控分数都会增加。这表明不同的头需要不同的稀疏性，凸显了头特定门控机制的重要性。

A.5 其他稳定训练的尝试

我们观察到，添加sandwich归一化（Ding et al., 2021）和门控机制都能消除大规模激活并提高训练稳定性。这促使我们探索是否可以使用更简单的方法来防止残差中的大激活。具体来说，我们引入了一个裁剪（clipping）操作，在注意力和FFN层的输出进入残差连接之前对其进行约束，将其值限制在(-clip, clip)范围内。然而，我们发现无论clip值设置为300还是100，模型在8e-3的学习率下仍然会遇到收敛问题。这表明预归一化（pre-norm）模型训练中的不稳定性不仅仅是由残差中的大激活引起的。任何产生大输出的层都可能导致稳定性问题，这表明需要进一步研究训练不稳定的根本原因。

在这里插入图片描述