当前位置： 首页 > news >正文

数据结构 之 【图的遍历与最小生成树】(广度优先遍历算法、深度优先遍历算法、Kruskal算法、Prim算法实现)

news 2025/9/29 5:43:42

目录

1.图的遍历

1.1图的广度优先遍历

实现思路

代码呈现

广度优先遍历（BFS）详解与评价

1.2图的深度优先遍历

实现思路

递归实现

递归实现深度优先遍历（DFS）详解与评价

栈实现

栈实现DFS算法实现评价

2.最小生成树

2.1Kruskal算法

核心思想及演示

代码实现

Kruskal算法详解与评价

2.2Prim算法

核心思想及演示

代码实现

Prim算法详解与评价

3.上述总结

4. 底层数据结构分析

空间复杂度：稀疏图的天然适配

时间效率：遍历与边操作的优势

下述算法实现是在上一期邻接表实现图的代码基础上实现的

1.图的遍历

给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思

1.1图的广度优先遍历

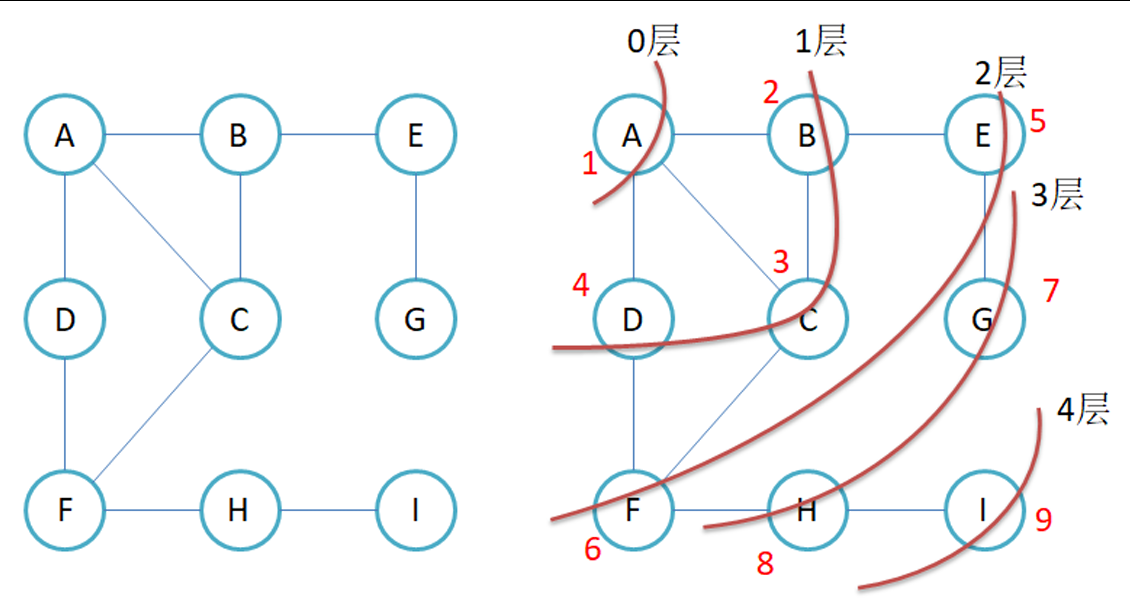
核心思想：从起点出发，先访问所有邻接顶点，再逐层向外扩展（类似水波纹扩散）

实现思路

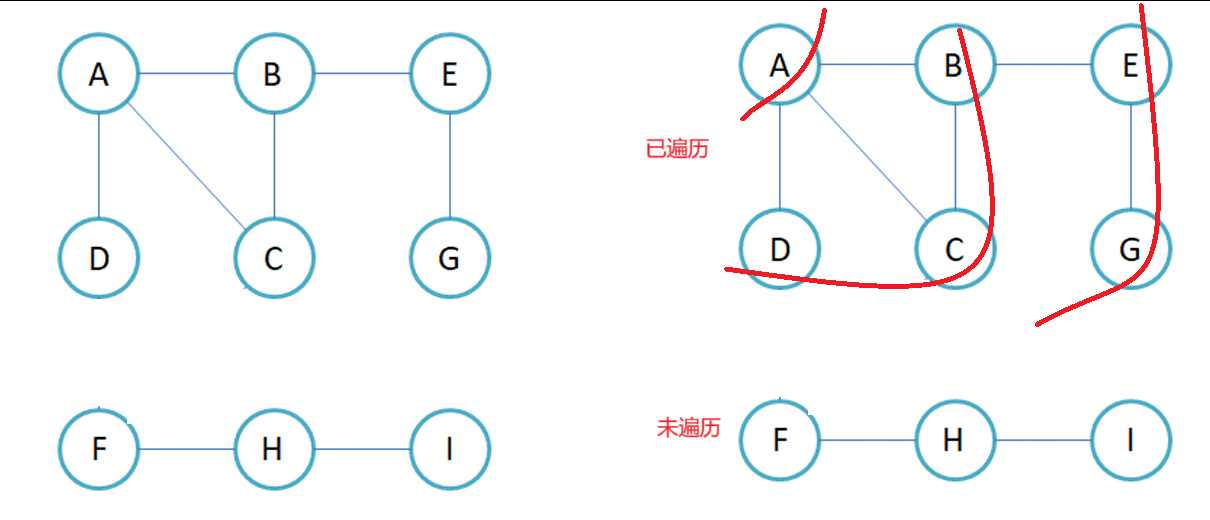
(1)将给定起点入队列，并标记为入队列

(2)访问、出队头元素之后，将与队头元素相连的未被标记过的顶点入队列

(3)重复步骤2，直到队列为空为止

元素入队列就进行标记，那么就可以防止同一元素多次入队列

当出队头元素B时，与B相连的定点有A、C、E

A、C已经入队列了，就没有必要再入了

队列为空标志着给定起点所在的联通分量被遍历完

代码呈现

(1)实现铺垫：队列、标记数组

	void BFS(const V& src){int n = _vertexes.size();int srci = GetIndexOfVertexes(src);//队列和标记数组queue<int> q;vector<bool> visited(n, false);//进队列就标记，防止同一元素多次入队列q.push(srci);visited[srci] = true;//..}

(2)遍历逻辑

    while (!q.empty()){//访问队头元素int front = q.front();q.pop();cout << front << " : " << _vertexes[front] << ' ';//所连接的未被访问过的顶点入队列Edge* cur = _tables[front];while (cur){if (visited[cur->_dsti] == false){q.push(cur->_dsti);visited[cur->_dsti] = true;}cur = cur->_next;}}

(1)队列不为空，说明还有顶点未被访问

(2)先访问队头元素(这里打印顶点下标及顶点)

(3)所连接的未被访问过的顶点入队列

  • 这里选择用邻接表查找未被访问过的顶点而不时邻接矩阵，是因为即使两顶点不相连，在遍历邻接矩阵的过程中也可能被访问，这就造成了效率损失(访问大量不存在的边时)

(4)直到队列为空，给定起点所在的联通分量被遍历完

(3)完整实现

//广度优先遍历
//从一个顶点出发，访问它所连接的未被访问过的顶点
void BFS(const V& src)
{int n = _vertexes.size();int srci = GetIndexOfVertexes(src);//队列和标记数组queue<int> q;vector<bool> visited(n, false);//进队列就标记，防止同一元素多次入队列q.push(srci);visited[srci] = true;//每层的个数int levelsize = 1;//开始遍历while (!q.empty()){//一层一层的出for (int i = 0; i < levelsize; ++i){	//访问队头元素int front = q.front();q.pop();cout << front << " : " << _vertexes[front] << ' ';//所连接的未被访问过的顶点入队列Edge* cur = _tables[front];while (cur){if (visited[cur->_dsti] == false){q.push(cur->_dsti);visited[cur->_dsti] = true;}cur = cur->_next;}}cout << endl;levelsize = q.size();}
}

广度优先遍历（BFS）详解与评价

实现逻辑：基于队列实现，按层扩展访问范围。在邻接表中，通过队列管理顶点访问顺序，利用levelsize控制层序输出。
时间复杂度：O(V+E)，与DFS相同但空间复杂度更高（队列需存储O(V)顶点）。
优点：

  • 天然适合最短路径问题（如无权图）。
  • 层序遍历特性利于网络爬虫、社交网络层级扩散等场景。

缺点：

  • 内存占用大（队列存储所有待访问顶点）。
  • 路径记录复杂（需额外存储父节点信息）。
    适用场景：无权图最短路径、网络爬虫、社交网络分析、连通分量检测。

1.2图的深度优先遍历

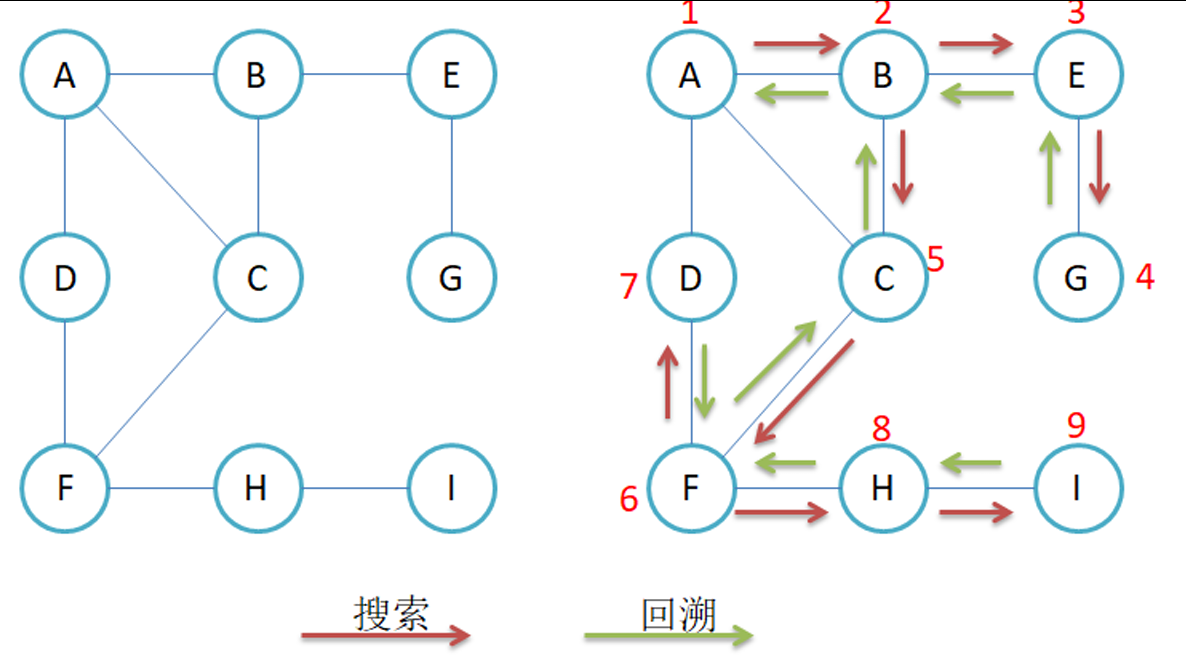
核心思想：从起点出发，沿着一条路径尽可能深地访问，直到无法继续（遇到已访问顶点或死胡同），然后回溯到上一个分支点继续探索

实现思路

(1)从给定起点出发，访问当前节点

(2)然后访问与当前节点相连的未被访问过的任一节点(一般是存储时的第一个点，访问过了就往后找)

(3)重复步骤2，直到与当前节点相连的节点都被访问过后，回溯到之前的某一节点

该节点的特点是：仍有相连的未被访问过的节点

(4)再从与该节点相连的未被访问过的任一节点出发，访问这任一节点

(5)重复步骤3，直到所有点都被访问过


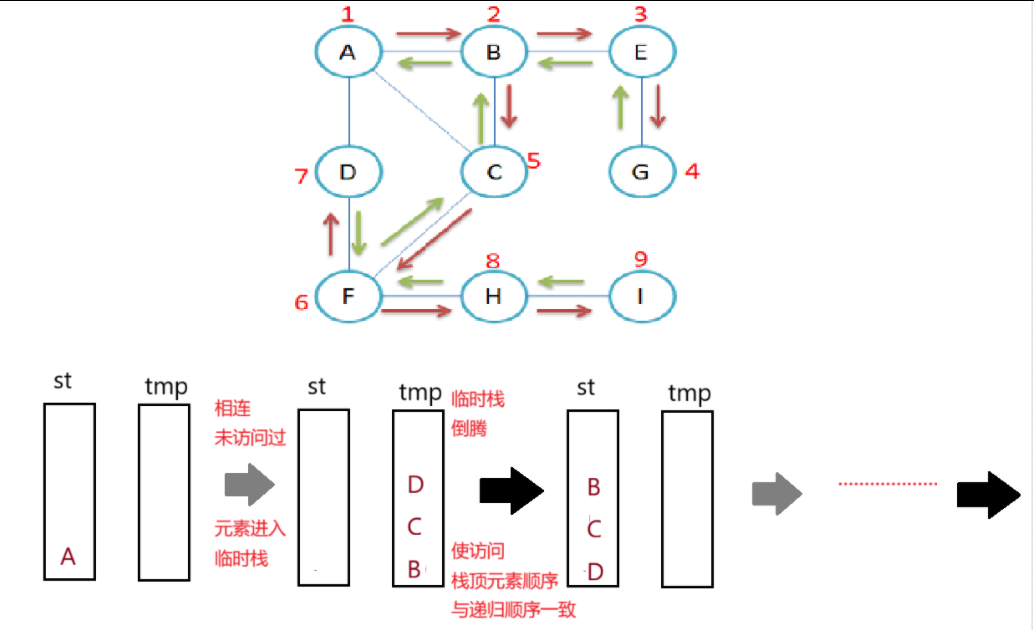
访问A节点，B与A相连且未被访问                                                                                步骤1
访问B节点，E与B相连且未被访问                                                                                步骤2
访问E节点，G与E相连且未被访问                                                                                步骤2
访问G节点，与G节点相连的所有节点都被访问过，开始回溯G->E->B                        步骤3   
与B节点相连的C节点仍未被访问
访问C节点，F与C相连且未被访问                                                                                步骤4
访问F节点，D与F相连且未被访问                                                                                步骤2
访问D节点，与D节点相连的所有节点都被访问过，开始回溯D->F                               步骤3
与F节点相连的H节点仍未被访问
访问H节点，I与H相连且未被访问                                                                                步骤4
访问I节点，与I节点相连的所有节点都被访问过，开始回溯I->H->F->C->B->A           步骤3    
直到所有点都被访问过，遍历结束
递归实现

(1)求给定顶点的下标、创建标记数组，调用子函数

void DFS(const V& src)
{int n = _vertexes.size();int srci = GetIndexOfVertexes(src);vector<bool> visited(n, false);_DFS(srci, visited);
}

(2)子函数

void _DFS(int srci, vector<bool>& visited)
{//访问并标记cout << srci << " : " << _vertexes[srci] << endl;visited[srci] = true;//访问下一个相连但未访问过Edge* cur = _tables[srci];while (cur){if (visited[cur->_dsti] == false)_DFS(cur->_dsti, visited);cur = cur->_next;}
}

(1)访问当前节点并标记

(2)访问与当前节点相连但未访问过的顶点

  • 选择用邻接表查找未被访问过的顶点而不是邻接矩阵，这是因为矩阵有大量不存在的边时，在遍历邻接矩阵的过程会就造成了效率损失(访问大量不存在的边)

(3)完整呈现

		//栈溢出风险void DFS(const V& src){int n = _vertexes.size();int srci = GetIndexOfVertexes(src);vector<bool> visited(n, false);_DFS(srci, visited);}void _DFS(int srci, vector<bool>& visited){//立即访问并标记cout << srci << " : " << _vertexes[srci] << endl;visited[srci] = true;//访问下一个相连但未访问过Edge* cur = _tables[srci];while (cur){if (visited[cur->_dsti] == false)_DFS(cur->_dsti, visited);cur = cur->_next;}}
递归实现深度优先遍历（DFS）详解与评价

实现逻辑：基于递归/栈实现，从起点出发沿一条路径深入探索，直到无法前进时回溯。在邻接表结构中，通过_DFS函数递归访问相邻顶点，利用visited数组避免重复访问。

时间复杂度：O(V+E)（顶点数+边数），每个顶点和边各访问一次。

优点：

  • 空间效率高（递归深度仅需O(V)），适合树或深度较大的图。
  • 路径探索直观，适合寻找连通分量、拓扑排序等。

缺点：

  • 递归可能导致栈溢出（如代码中_DFS的栈深度风险）。
  • 非最优路径搜索（如最短路径需结合BFS）。
  • 适用场景：连通性检测、迷宫问题、拓扑排序、强连通分量。
栈实现

(1)给定起点入栈并标记，初始化标记数组

void DFS(const V& src)
{int n = _vertexes.size();int srci = GetIndexOfVertexes(src);stack<int> st;stack<int> tmp;//临时栈vector<bool> visited(n, false);//入栈就标记，防止同一元素多次入栈st.push(srci);visited[srci] = true;//遍历
}

(2)

while (!st.empty())
{//访问栈顶元素int top = st.top();st.pop();cout << top << ":" << _vertexes[top] << endl;//关联的未访问过的顶点全入栈Edge* cur = _tables[top];while (cur){if (visited[cur->_dsti] == false){tmp.push(cur->_dsti);}cur = cur->_next;}//逆序入栈，与递归访问顺序一致while (!tmp.empty()){int top = tmp.top();tmp.pop();visited[top] = true;st.push(top);}
}

(1)访问栈顶元素并出栈

(2)与栈顶元素相连的未被标记的元素全部入临时栈

(3)临时栈中元素导入栈中

(4)重复步骤123，直到栈中元素为空，遍历结束

  • 实现过程

  • 临时栈是为了倒腾顶点，调整访问顺序与递归访问时顺序一致
栈实现DFS算法实现评价

正确性：该DFS实现逻辑严谨，通过双栈机制（主栈st+临时栈tmp）实现了与递归DFS完全一致的深度优先访问顺序。关键优化点在于：

  • 使用tmp栈反转邻接顶点顺序，确保主栈st的弹出顺序符合深度优先特性（如邻接表存储A→B→C时，实际访问顺序为C→B→A）。
  • 入栈时立即标记visited，避免重复访问，时间复杂度严格为O(V+E)（V顶点数，E边数）。

潜在问题：

  • 不连通图处理缺失：仅能遍历起始顶点所在连通分量，需外层补充循环处理多连通分量（如for(v∈V) if(!visited[v]) DFS(v)）。
  • 顶点输出顺序：当前实现按访问顺序输出顶点，若需路径记录需额外存储父节点关系（如parent数组）

2.最小生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，

即：从其中删去任何一条边，生成树 就不再连通；反之，在其中引入任何一条新边，都会形成一条回路。 若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。

因此构造最小生成树的准则有三 条：

  • 1. 只能使用图中的边来构造最小生成树
  • 2. 只能使用恰好n-1条边来连接图中的n个顶点
  • 3. 选用的n-1条边不能构成回路

构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。

  • 贪心算法：是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是 整体 最优的的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优 解。

2.1Kruskal算法

核心思想及演示

核心思想：按边的权值从小到大排序，依次选择权值最小且不形成环的边，直到生成树包含所有顶点

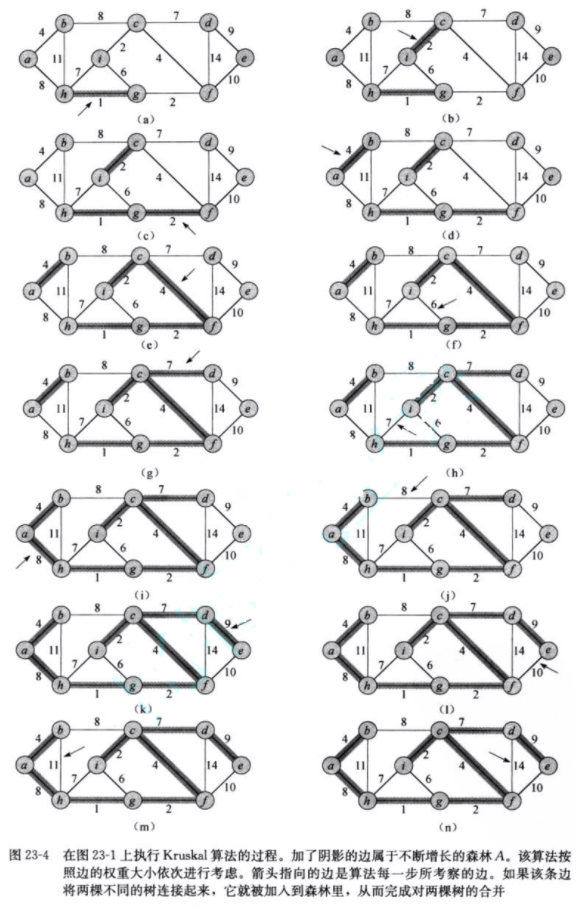
代码实现

(1)最小生成树是图的子图，拥有与图相同的顶点

typedef graph<V, W, Direction> self;

(2)使用优先级队列存储边，就可以依次选择权值最小的边

(3)使用并查集，进入最小生成树的顶点在同一个集合当中

W Kruskal(self& minTree)
{int n = _vertexes.size();minTree._index = _index;minTree._vertexes = _vertexes;minTree._tables.resize(n, nullptr);//优先级队列存储边priority_queue<Edge, vector<Edge>, greater<Edge>> minpq;for (int i = 0; i < _tables.size(); ++i){//无向图的邻接表中，边存了双份Edge* cur = _tables[i];while (cur){minpq.push(*cur);cur = cur->_next;}}UnionFindSet ufs(n);//权值和、边数W totalw = W();int size = 0;//开始选边}

(4)开始选边

//开始选边
while (!minpq.empty())
{//选出最小边Edge min = minpq.top();minpq.pop();//判环if (ufs.InSet(min._srci, min._dsti)){cout << "构成环：" << _vertexes[min._srci] << "->" << _vertexes[min._dsti]<< ":" << min._w << endl;continue;}//进入最小生成树minTree._AddEdge(min._srci, min._dsti, min._w);cout << _vertexes[min._srci] << "->" << _vertexes[min._dsti]<< ":" << min._w << endl;//进入最小生成树的顶点在同一个集合ufs.Union(min._srci, min._dsti);++size;totalw += min._w;if (size == n - 1)break;
}
if (size == n - 1)return totalw;
else return W();

(1)优先级队列不为空，就继续选边

(2)当前权值最小的边的两个顶点不能在并查集中，否则就会构成环

(3)当前权值最小的边的两个顶点不在并查集中，该边就进入最小生成树

(4)更新并查集、边数、权值和

(5)选够n - 1条边就跳出循环

(6)根据边数返回值

完整实现

//开始选边
while (!minpq.empty())
{//选出最小边Edge min = minpq.top();minpq.pop();//判环if (ufs.InSet(min._srci, min._dsti)){cout << "构成环：" << _vertexes[min._srci] << "->" << _vertexes[min._dsti]<< ":" << min._w << endl;continue;}//进入最小生成树minTree._AddEdge(min._srci, min._dsti, min._w);cout << _vertexes[min._srci] << "->" << _vertexes[min._dsti]<< ":" << min._w << endl;//进入最小生成树的顶点在同一个集合ufs.Union(min._srci, min._dsti);++size;totalw += min._w;if (size == n - 1)break;
}
if (size == n - 1)return totalw;
else return W();

Kruskal算法详解与评价

实现逻辑：贪心策略+并查集判环。将所有边按权重升序排序，逐个添加边到最小生成树（MST），通过并查集检测环。代码中priority_queue存储边，UnionFindSet实现连通性判断。
时间复杂度：O(E log E)（排序耗时），并查集操作近似O(α(V))。

空间复杂度：

  1. 核心数据结构：
  2. 优先队列（最小堆）：存储所有边，空间复杂度O(E)。
  3. 并查集：存储顶点集合关系，空间复杂度O(V)（父指针数组+秩数组）。
  4. 最小生成树存储：邻接表需O(V+E)空间（顶点+边）。
  5. 辅助空间：visited数组O(V)，临时变量O(1)。
  6. 总空间复杂度：O(E + V)
  7. （边排序占主导，适合稀疏图E≪V²）

优点：

  • 适合稀疏图（边数远小于顶点数平方）。
  • 算法逻辑清晰，易于实现分布式计算。

缺点：

  • 需存储所有边并排序，空间开销大。
  • 并查集实现复杂度影响性能（路径压缩可优化）。
    适用场景：稀疏图的最小生成树、网络规划、电路设计

2.2Prim算法

核心思想及演示

核心思想：从一个顶点开始，逐步扩展生成树，每次选择连接树内顶点和树外顶点的最小权值边

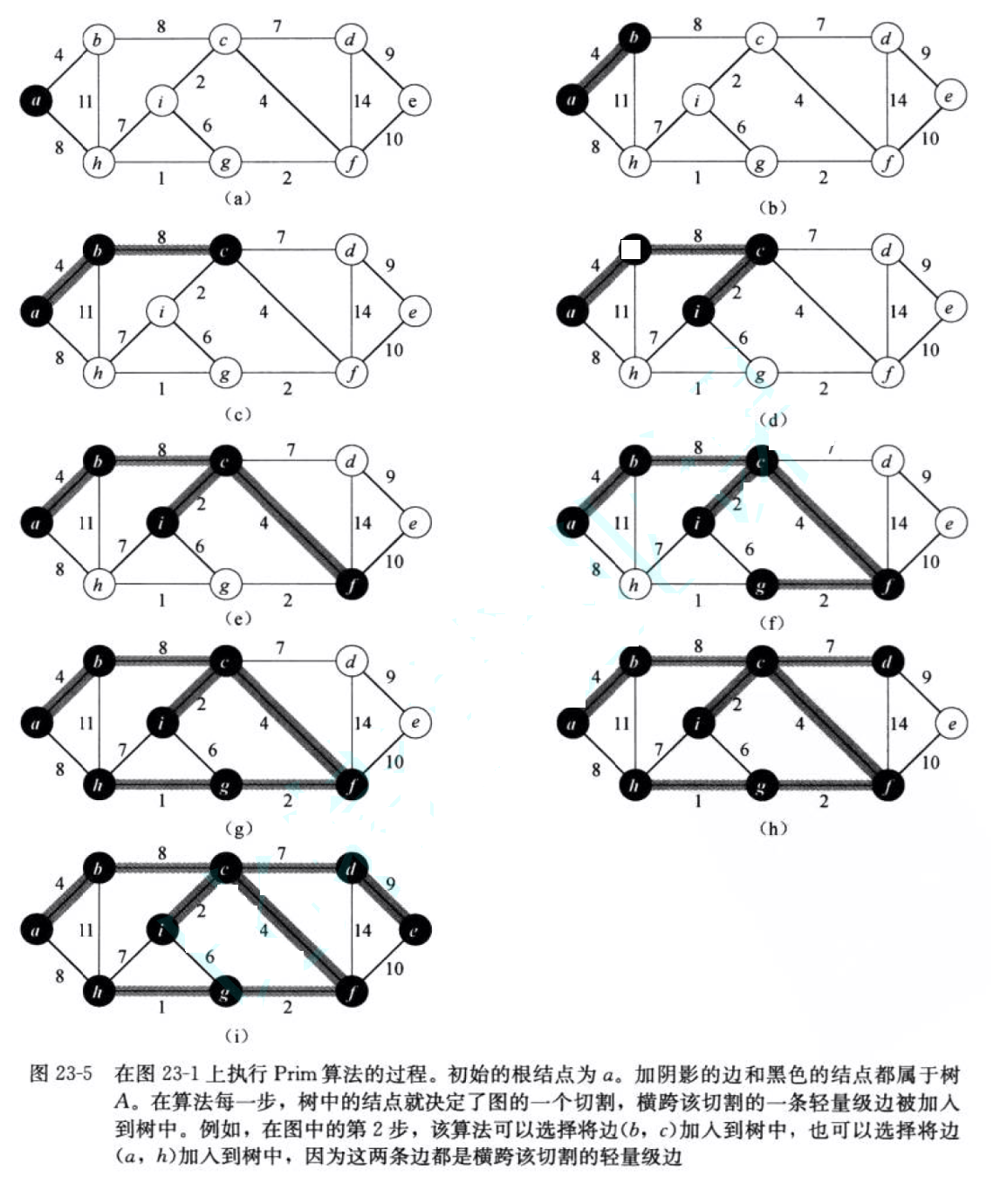
代码实现

(1)最小生成树是图的子图，拥有与图相同的顶点

typedef graph<V, W, Direction> self;

(2)使用标记容器，区分树内与树外的顶点

(3)使用优先级队列存储边，就可以依次选择从树内顶点到树外顶点中权值最小的边

W Prim(self& minTree, const V& src)
{int srci = GetIndexOfVertexes(src);int n = _vertexes.size();minTree._index = _index;minTree._vertexes = _vertexes;minTree._tables.resize(n, nullptr);//在最小生成树中的顶点vector<bool> in(n, false);in[srci] = true;//优先级队列存储边priority_queue<Edge, vector<Edge>, greater<Edge>> minpq;//从当前节点连接出去的边//无向图的邻接表中Edge* cur = _tables[srci];while (cur){minpq.push(*cur);cur = cur->_next;}//权值、边数W totalw = W();int size = 0;//开始选边
]

(2)开始选边

//开始选边
while (!minpq.empty())
{//选出最小边Edge min = minpq.top();minpq.pop();//判环if (in[min._dsti] == true){cout << "构成环：" << _vertexes[min._srci] << "->" << _vertexes[min._dsti]<< ":" << min._w << endl;continue;}//进入最小生成树minTree._AddEdge(min._srci, min._dsti, min._w);cout << _vertexes[min._srci] << "->" << _vertexes[min._dsti]<< ":" << min._w << endl;//进入最小生成树的顶点in[min._dsti] = true;++size;totalw += min._w;if (size == n - 1)break;//先做上述判断，再持续进边Edge* cur = _tables[min._dsti];while (cur){//边的顶点不再最小生成树内if(in[cur->_dsti] == false)minpq.push(*cur);cur = cur->_next;}
}
if (size == n - 1)return totalw;
else return W();

(1)优先级队列不为空，就继续选边

(2)当前权值最小的边的尾顶点不能在树中，否则就会构成环

  • 仅需判断边的尾节点，因为优先级队列中的边的头节点都在最小生成树中

(3)当前权值最小的边的尾顶点不在树中，该边就进入最小生成树

(4)更新标记数组、边数、权值和

(5)选够n - 1条边就跳出循环，否则将以当前边的尾节点为头节点的边入优先级队列

(6)根据边数返回值

Prim算法详解与评价

实现逻辑：从起点扩展，逐步连接新顶点。维护优先队列存储候选边，每次选择最小边连接已选顶点和未选顶点。代码中priority_queue动态更新候选边，in数组标记已选顶点。
时间复杂度：O(E log V)（优先队列操作），稠密图下优于Kruskal。

空间复杂度：

  1. 核心数据结构：
  2. 优先队列（最小堆）：动态存储候选边，最坏情况O(E)（每条边可能被插入一次）。
  3. 标记数组in[]：记录顶点是否在生成树中，空间O(V)。
  4. 最小生成树存储：邻接表需O(V+E)空间。
  5. 辅助空间：邻接表遍历指针O(1)，临时变量O(1)。
  6. 总空间复杂度：O(E + V)
  7. （优先队列占主导，适合稠密图E≈V²）

优点：

  • 适合稠密图（边数接近顶点数平方）。
  • 无需全局排序，动态维护候选边更高效。

缺点：

  • 优先队列实现复杂（如斐波那契堆可优化但代码复杂）。
  • 初始顶点选择影响收敛速度。
    适用场景：稠密图的最小生成树、图像分割、聚类分析。

3.上述总结

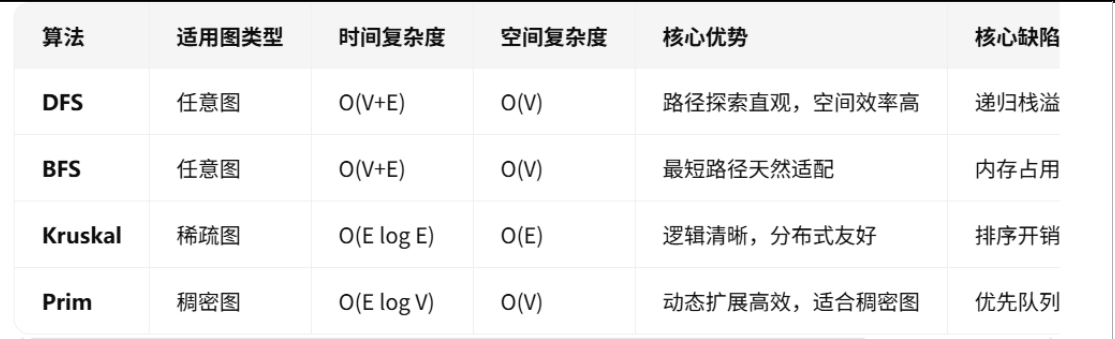
4. 底层数据结构分析

在图的遍历与最小生成树算法（如DFS、Kruskal、Prim）中，选择邻接表而非邻接矩阵作为底层数据结构可以从时空复杂度来分析

空间复杂度：稀疏图的天然适配

  • 邻接矩阵：空间复杂度为O(V²)（V为顶点数），无论图的稀疏或稠密，均需分配固定大小的二维数组。例如，1000个顶点的图需存储10⁶个元素，即使实际边数仅100条。
  • 邻接表：空间复杂度为O(V+E)（E为边数），仅存储实际存在的边。稀疏图（E≪V²）中优势显著，如1000顶点、1000边的图仅需约2000个存储单元（顶点+边），远优于邻接矩阵的百万级开销。
  • 适用场景：现实网络（如社交网络、交通网络）多为稀疏图，邻接表的空间经济性使其成为首选。

时间效率：遍历与边操作的优势

  • DFS的邻接顶点遍历：
    • 邻接表：遍历顶点v的所有邻接顶点需O(deg(v))时间（deg(v)为v的度数），总时间复杂度O(V+E)，与图结构自然匹配。
    • 邻接矩阵：需遍历v的整行（或列），耗时O(V)，即使实际邻接顶点极少（如度数为10），导致总时间O(V²)，效率低下。
  • Kruskal的边处理：
    • 邻接表：可高效遍历所有边（如通过链表或迭代器），时间O(E)，便于排序或插入优先队列。
    • 邻接矩阵：需双层循环遍历矩阵（O(V²)），提取边集的耗时占主导，尤其在稀疏图中劣势明显。
  • Prim的边选择：
    • 邻接表：可快速访问顶点v的邻接边（O(deg(v))），便于动态更新优先队列。
    • 邻接矩阵：访问v的邻接边需O(V)时间，影响优先队列的更新效率。
http://www.dtcms.com/a/418130.html

相关文章：

  • 胶州做网站的做网站设计有哪些网页
  • 开源 C# 快速开发（十）通讯--http客户端
  • 如何用 ShedLock 让 Spring Boot 的定时任务在多实例环境下只执行一次
  • Mask R-CNN工业落地实战：计算机视觉物体检测开山鼻祖的产线级代码剖析
  • 沈阳网站制作全网性做橡胶的网站
  • C++压缩解压：Zstandard (Zstd)压缩库
  • 在网站建设中 为了防止工期拖延荥阳网站制作
  • Filebeat写ElasticSearch故障排查思路（下）
  • 禅道数据还原
  • 货架 网站建设 牛商网网站设计目的与规划怎么写
  • 基于STM32设计的环境监测系统(华为云IOT)_300
  • OPPO手机“绿线”问题争议，高价等于高端，何以分食iPhone市场？
  • 国产之光！金仓数据库KingbaseES Oracle兼容性深度体验大赏
  • wordpress付费插件网站垂直门户网站的盈利模式探讨
  • Navicat 技术指引 | KingbaseES 逆向工程与正向工程
  • C#：将Excel转换为HTML时将图像嵌入HTML中
  • 滨州医学院做计算机作业的网站电商网站 模板
  • 访问控制、用户认证、https
  • 大语言模型在金融风控中的应用
  • 深圳培训公司网站建设辽宁市营商环境建设局网站
  • Activity 管理工具类（兼容 Android 16+ / API 16）
  • 【2026计算机毕业设计】基于Springboot的Android校园周边美食汇系统
  • 网站换主推关键词会怎么样网站建设年度报告
  • 软装设计公司网站网站设计怎么做背景颜色
  • 陕西网站建设公司找哪家网站建设需要花多少钱
  • 开封做网站公司导航网站备案
  • 如何判断网站程序使用asp还是php网站开发 架构设计
  • 网站开发 北京外包公司文档生成器app
  • 淘宝京东网站建设目的查找全国免费网站建设
  • wordpress网站前台密码网页设计一个网站