设计站什么是二次开发

背包问题

0-1背包问题

分析问题：每件物品只能使用一次，只有两种情况，放入背包或者不放入

其中第i件物品的体积为vi，价值为wi

求怎么放才能使得物品的总体积不超过背包容量，且总价值最大

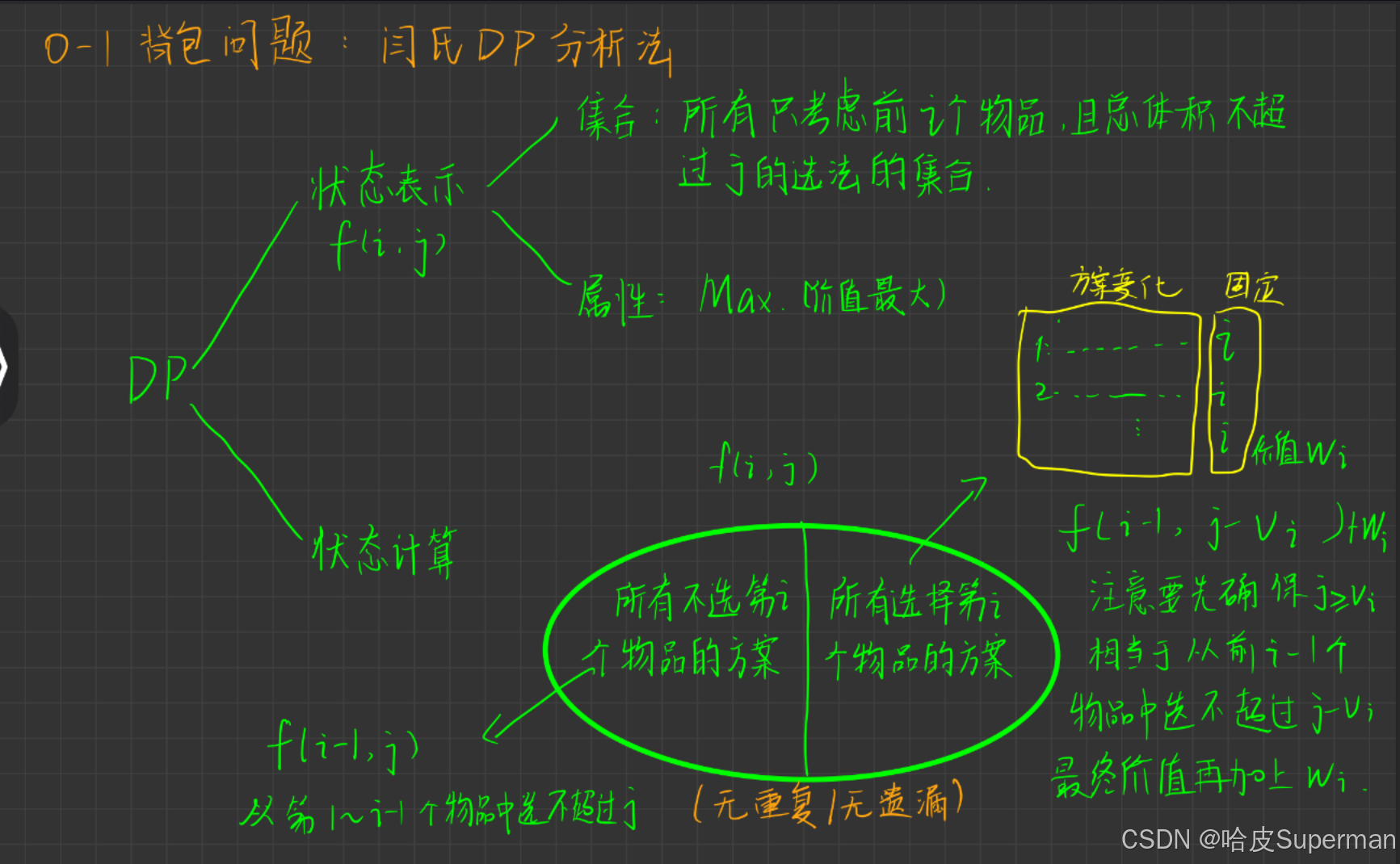
闫氏DP分析法：

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。在下图状态表示中，第一维一般是数量，第二维一般是限制 比如重量啊，体积啊

集合划分是指选择最后一个物品的方法

公式：f(i , j) = max( f(i - 1, j), f(i - 1, j - vi) + wi ) 可以变一维 优化空间

注意只要符合右侧子集的进入条件，就需要和左子集取max

最终结果 f[n][m]

#include <iostream>using namespace std;const int N = 1010;
int n, m;    // n件物品  m为背包容量
int v[N], w[N];   // 体积和权重
int f[N][N];   // DP 二维数组int main(){cin >> n >> m;for (int i = 1; i <= n; i ++){cin >> v[i] >> w[i];}for (int i = 1; i <= n; i ++){// 容量切分for (int j = 0; j <= m; j ++){// 左边f[i][j] = f[i - 1][j];// 右边 首先要确保容量条件  注意 只要进入了 就有左右两个值 所以需要取maxif (j >= v[i]){f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);}}}cout << f[n][m];
}

优化为一维数组，这里注意 DP问题的所有优化 都是针对代码层面进行优化，和问题本质没有关联

二维变一维 滚动数组

#include <iostream>using namespace std;const int N = 1010;
int n, m;    // n件物品  m为背包容量
int v[N], w[N];   // 体积和权重
// int f[N][N];   // DP 二维数组
int f[N];int main(){cin >> n >> m;for (int i = 1; i <= n; i ++){cin >> v[i] >> w[i];}for (int i = 1; i <= n; i ++){// 容量切分// for (int j = 0; j <= m; j ++){for (int j = m; j >= 0; j --){// 左边// f[i][j] = f[i - 1][j];f[j] = f[j];  // 这是没有问题的 因为i - 1是上一层的 这里也没有更新// 右边 首先要确保容量条件  注意 只要进入了 就有左右两个值 所以需要取maxif (j >= v[i]){// f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);  这里j - v[i] 比j小 此时j是从小到大进行的  所以j - v[i] 之前算过了// 但是我们需要先算f[j] 调整一下j的循环顺序就好了f[j] = max(f[j], f[j - v[i]] + w[i]);}}}cout << f[n][m];
}

整理一下最简：

#include <iostream>using namespace std;const int N = 1010;
int n, m;    // n件物品  m为背包容量
int v[N], w[N];   // 体积和权重
// int f[N][N];   // DP 二维数组
int f[N];int main(){cin >> n >> m;for (int i = 1; i <= n; i ++){cin >> v[i] >> w[i];}for (int i = 1; i <= n; i ++){// 容量切分// for (int j = 0; j <= m; j ++){for (int j = m; j >= v[i]; j --){f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m];
}

完全背包问题

区分0-1背包：这个每种物品可以用无限次

代码：

/*** 1. 0-1背包：  f[i][j] = max(f[i - 1][j], f[i - 1][j - v] + w);* 2. 完全背包： f[i][j] = max(f[i - 1][j], f[i][j - v] + w);* 完全背包问题：* N 种物品  容量为V的背包  每种物品无限件可用* 第i种物品的体积是vi 价值是wi* 将哪些物品装入背包 总体积不超过背包容量  且总价值最大*/
#include <iostream>using namespace std;const int N  = 1010;   // 开数组int n, m;   // n 为物品种类数   m是背包容积
int v[N], w[N];   // 每个物品的体积和价值
int f[N][N];    // DP
int main(){cin >> n >> m;for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}// 实现f[i][j] = max(f[i - 1][j], f[i][j - v] + w);for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){// 第一个 此时 右边的式子不一定符合体积条件f[i][j] = f[i - 1][j];// 如果右边的存在if(j >= v[i]){f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);    }}}cout << f[n][m];return 0;
}

优化

#include <iostream>using namespace std;const int N  = 1010;   // 开数组int n, m;   // n 为物品种类数   m是背包容积
int v[N], w[N];   // 每个物品的体积和价值
int f[N];int main(){cin >> n >> m;for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}// 实现f[i][j] = max(f[i - 1][j], f[i][j - v] + w);for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){// 第一个 此时 右边的式子不一定存在// f[i][j] = f[i - 1][j];f[j] = f[j];  // 这个式子先算右边  所以这里的f[j]是上一层i的 所以和我们的i - 1等价// 如果右边的存在if(j >= v[i]){// f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);    当前i的 可以正向遍历f[j] = max(f[j], f[j - v[i]] + w[i]);   // 便于理解 可以从这个式子结果出发 反向推导是否等价 这里的右边f[j]是刚刚算的 所以等于是f[i - 1][j]// 右侧后面 j - v[i]是小于f[j]的 此时j从小到大 所以是第i层的}}}// 空间优化 二维变一维cout << f[m];return 0;
}