算法训练.16

目录

70 力扣 第N个泰波那契数

70.1 题目解析：

70.2 算法思路：

70.3 代码演示：

71 力扣 三步问题：

71.1 题目解析：

71.2 算法思路：

71.3 代码演示

72 力扣 最小花费爬楼梯

72.1 题目解析：

72.2 算法思路：

72.3 代码演示：

73 牛客网，杨辉三角

73.1 题目解析：

73.2 算法思路：

73.3 代码演示：

74 牛客网 孩子们的游戏（约瑟夫环问题）

74.1 题目解析：

74.2 算法思路

74.3 代码演示：

75 牛客网 简写单词

75.1 题目解析：

75.2 算法思路

75.3 代码演示：

76 牛客网 除2

76.1 题目解析：

76.2 算法思路：

76.3 代码演示

77 牛客网 Fibonacci数列

77.1 题目解析：

77.2 算法思路：

77.3 代码演示：

78 牛客网 游游的you

78.1 题目解析：

78.2 算法思路：

78.3 代码演示：

---

70 力扣 第N个泰波那契数

70.1 题目解析：

这道题目很好理解，并且，这道题目以及后面所讲的4道题目，都是“动态规划”相关的题目。

根据题意可知：这个的其实就是递推公式：T(n)=T(n-3)+T(n-2)+T(n-1)

70.2 算法思路：

这是解法，但是呢。咱们还可以使用滚动数组进行空间优化（一般背包问题可以用到）

70.3 代码演示：

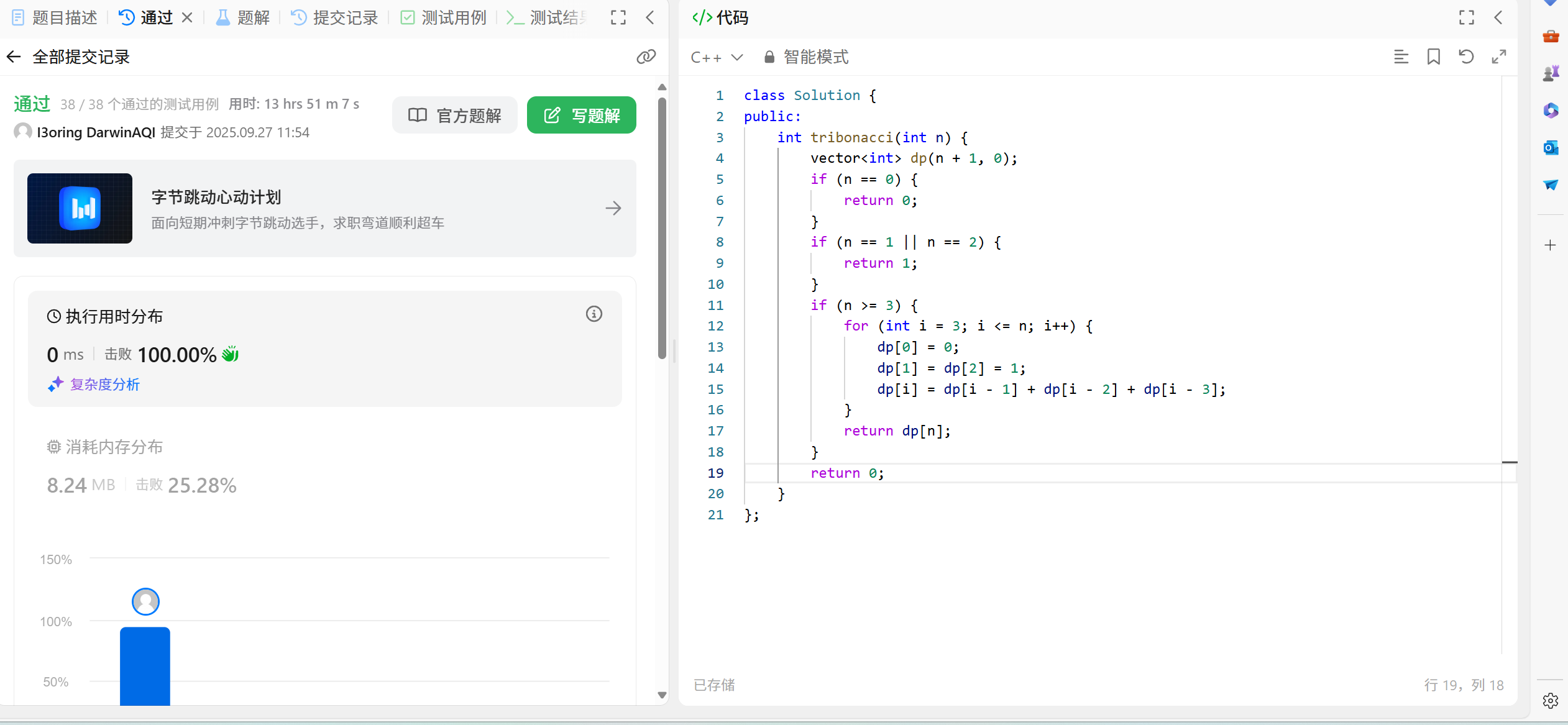
int tribonacci(int n) {vector<int> dp(n + 1, 0);//单独处理前3个数的情况if (n == 0) {return 0;}if (n == 1 || n == 2) {return 1;}if (n >= 3) {dp[0] = 0;dp[1] = dp[2] = 1;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];//核心代码其实是这个}return dp[n];}
}
int main()
{int n;cin >> n;cout << tribonacci(n) << endl;return 0;
}

空间优化：

int tribonacci(int n) {
vector<int> dp(n + 1, 0);
if (n == 0) {return 0;
}
if (n == 1 || n == 2) {return 1;
}
int a = 0, b = 1, c = 1, d = 0;//d可以随便赋值
if (n >= 3) {for (int i = 3; i <= n; i++) {d = a + b + c;//开始滚动a = b;b = c;c = d;}return d;
}
return 0;
}
int main()
{int n;cin >> n;cout << tribonacci(n) << endl;return 0;
}

71 力扣 三步问题：

71.1 题目解析：

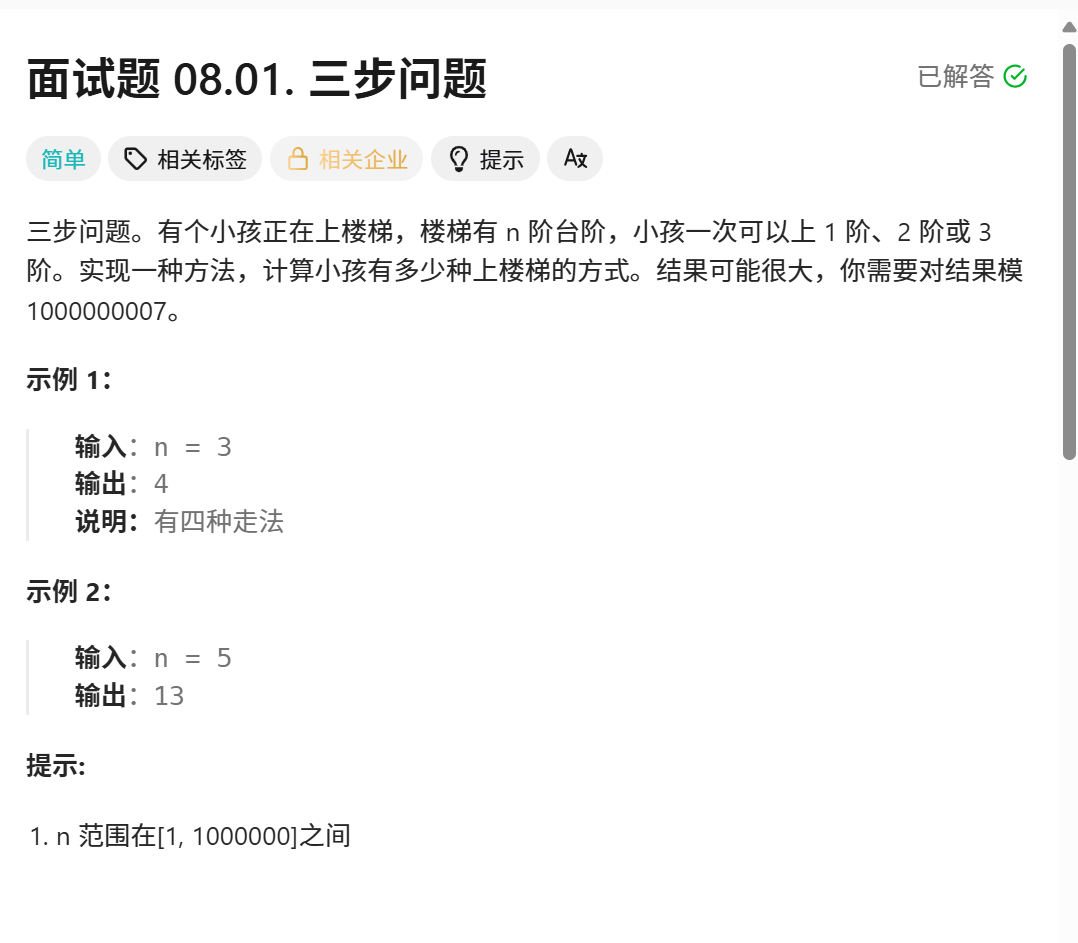
本题也是一道比较简单的动态规划的题目：

71.2 算法思路：

71.3 代码演示

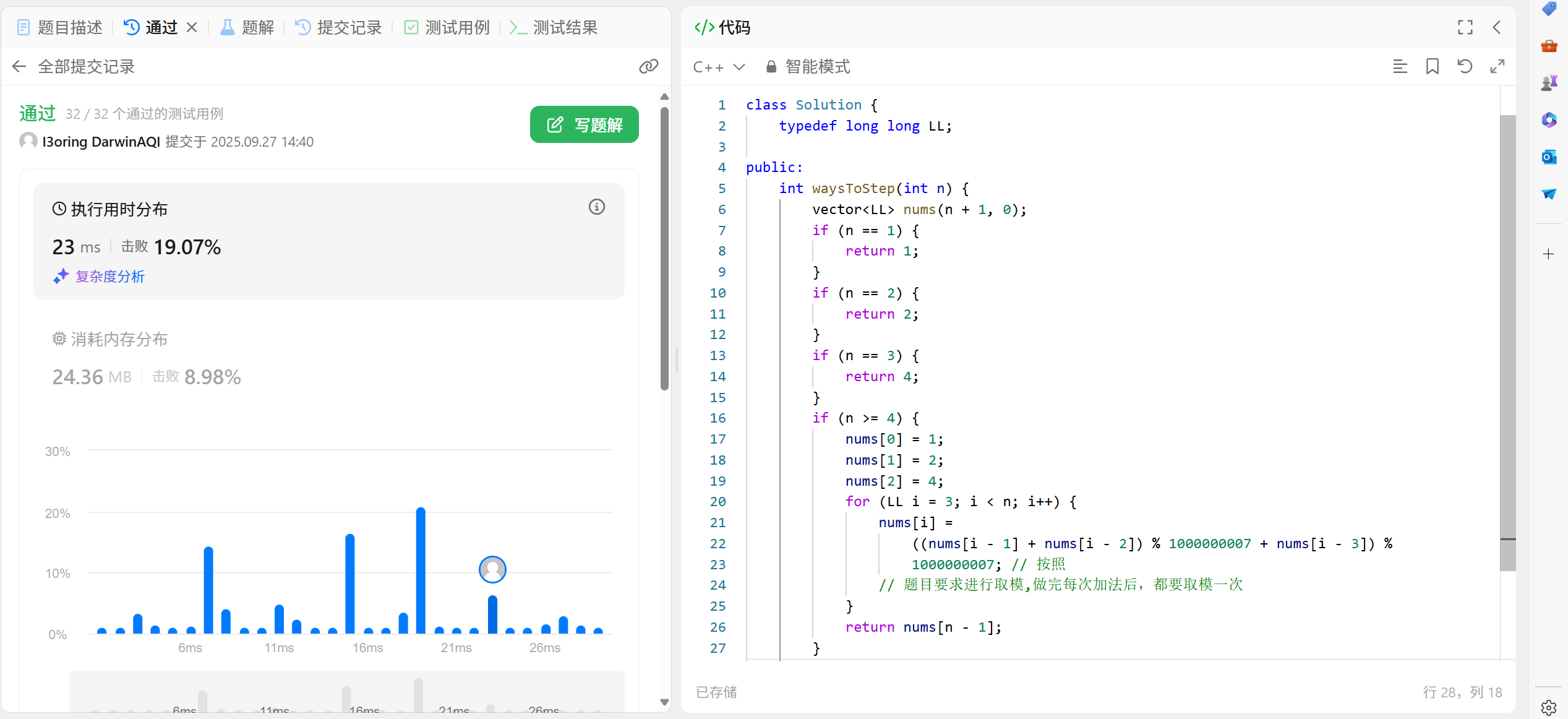
typedef long long LL;int waysToStep(int n) {vector<LL> nums(n + 1, 0);if (n == 1){return 1;}if (n == 2){return 2;}if (n == 3){return 4;}if (n >= 4){nums[0] = 1;nums[1] = 2;nums[2] = 4;for (LL i = 3; i < n; i++){nums[i] = ((nums[i - 1] + nums[i - 2] ) %1000000007 + nums[i - 3]) % 1000000007;//按照//题目要求进行取模,做完每次加法后，都要取模一次}return nums[n - 1];}
}

别忘了这里是需要进行取模的，并且，每次加完之后都要进行取模操作

72 力扣 最小花费爬楼梯

72.1 题目解析：

这道题目也是一道动态规划的题目，那么接下来就看我来给大家做解析吧

72.2 算法思路：

72.3 代码演示：

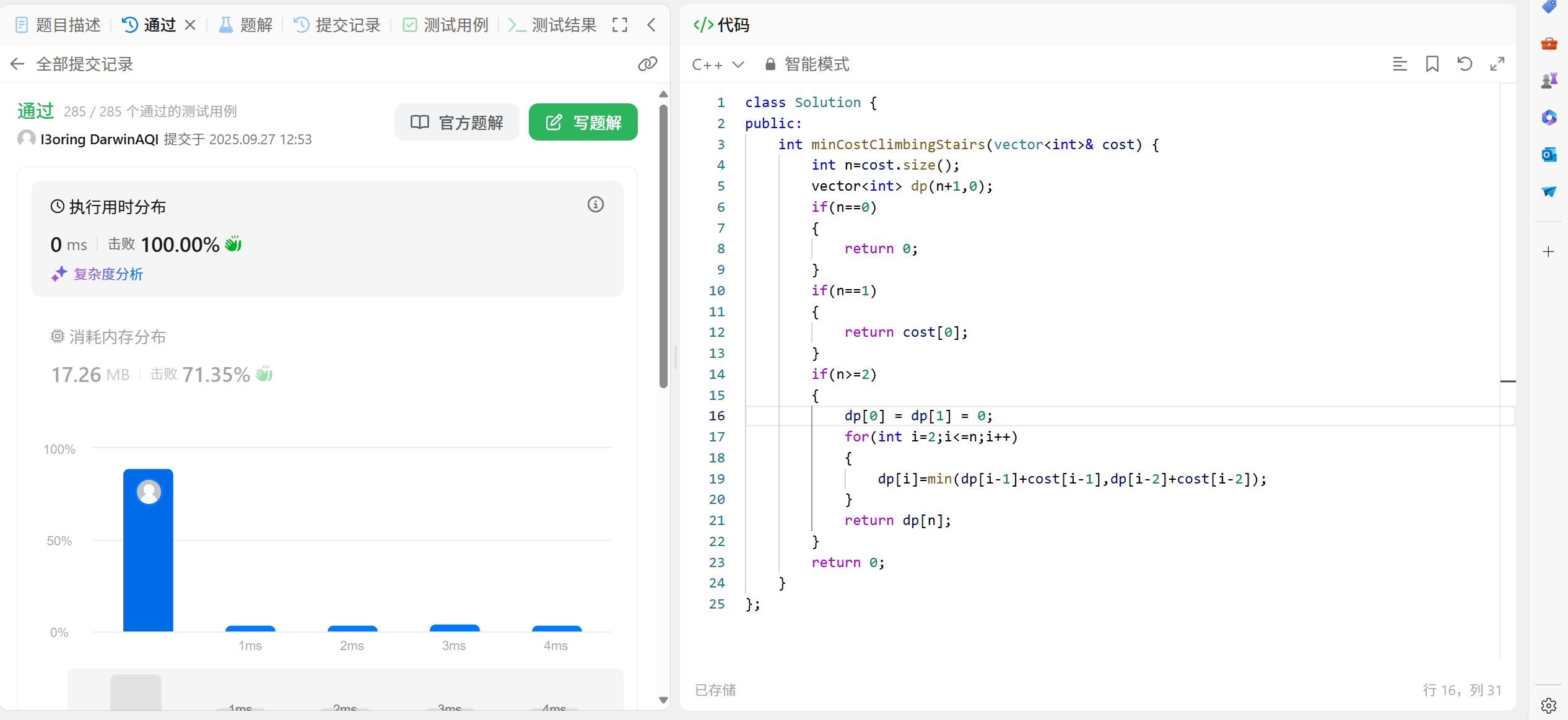
//最小花费爬楼梯
int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n + 1, 0);if (n == 0){return 0;}if (n == 1){return cost[0];}if (n >= 2){dp[0] = dp[1] = 0;for (int i = 2; i <= n; i++){dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[n];}
}
int main()
{vector<int> cost = { 1, 100, 1, 1, 1, 100, 1, 1, 100, 1 };cout << minCostClimbingStairs(cost) << endl;return 0;
}

73 牛客网，杨辉三角

73.1 题目解析：

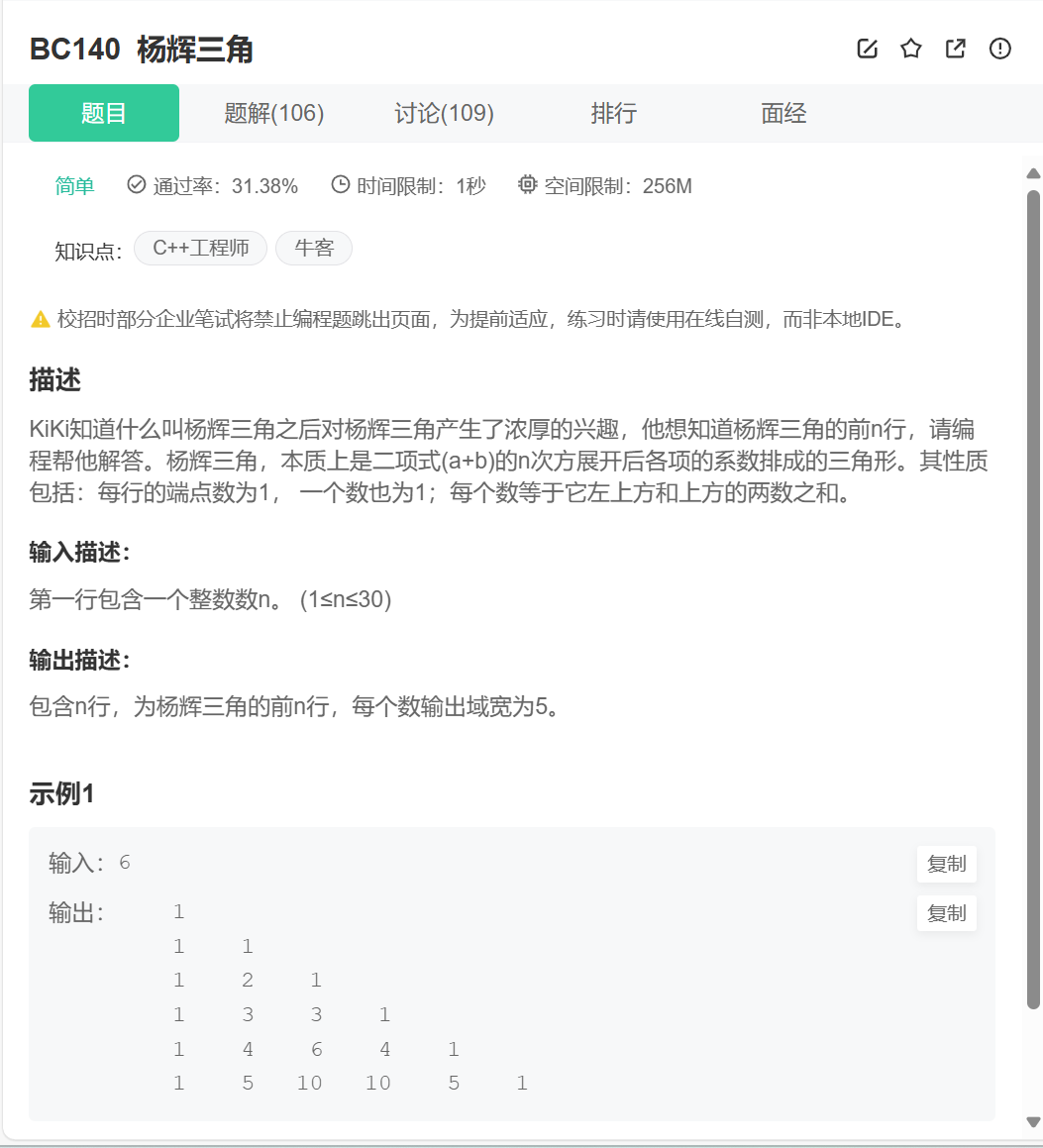
那么杨辉三角，大家想必很熟悉了吧。这个东西不管初中数学，高中数学都考过这个。那么下面我来给大家分析一下

73.2 算法思路：

这个地方，那么咱们的前后两个端口都是1.并且，咱们可以发现，第n行（n>=3)开始，每一行的中间的元素都是等于n-1行的对应元素与对应元素的前一个元素的和。每一个都是这样的。并且，n-1行的元素，都会被执行完毕

所以说，咱们可以得到状态转移方程：

nums[i][j] = nums[i - 1][j - 1] + nums[i - 1][j]

这个状态转移方程是关键啊！

那么这个是二维的，所以说填表的话，直接按照

二维的数组的进行填就可以了。

那么返回值，就是输出这个杨辉三角即可。

73.3 代码演示：

杨辉三角
#include <iostream>
using namespace std;int main() {int n;cin >> n;int nums[30][30] = { 0 };for (int i = 0; i < n; i++) {nums[i][0] = 1;//j<=i也是为了避免给咱们不需要的列赋值for (int j = 1; j <= i; j++) {nums[i][j] = nums[i - 1][j - 1] + nums[i - 1][j];}}for (int i = 0; i < n; i++) {//j<=i避免打印，不存在的列，比如i=3，n=5，你如果说j<5的话，那么nums[3][4]就是//不存在的列。j<n只适用于想把数组所有的元素都打印出来for (int j = 0; j <=i; j++) {//每个数输出域宽为5printf("%5d", nums[i][j]);}cout << endl;}return 0;
}

这个地方，注意咱们的j都是小于等于i的，因为

这一块空白的地方，咱们并不需要这个代码。

74 牛客网 孩子们的游戏（约瑟夫环问题）

74.1 题目解析：

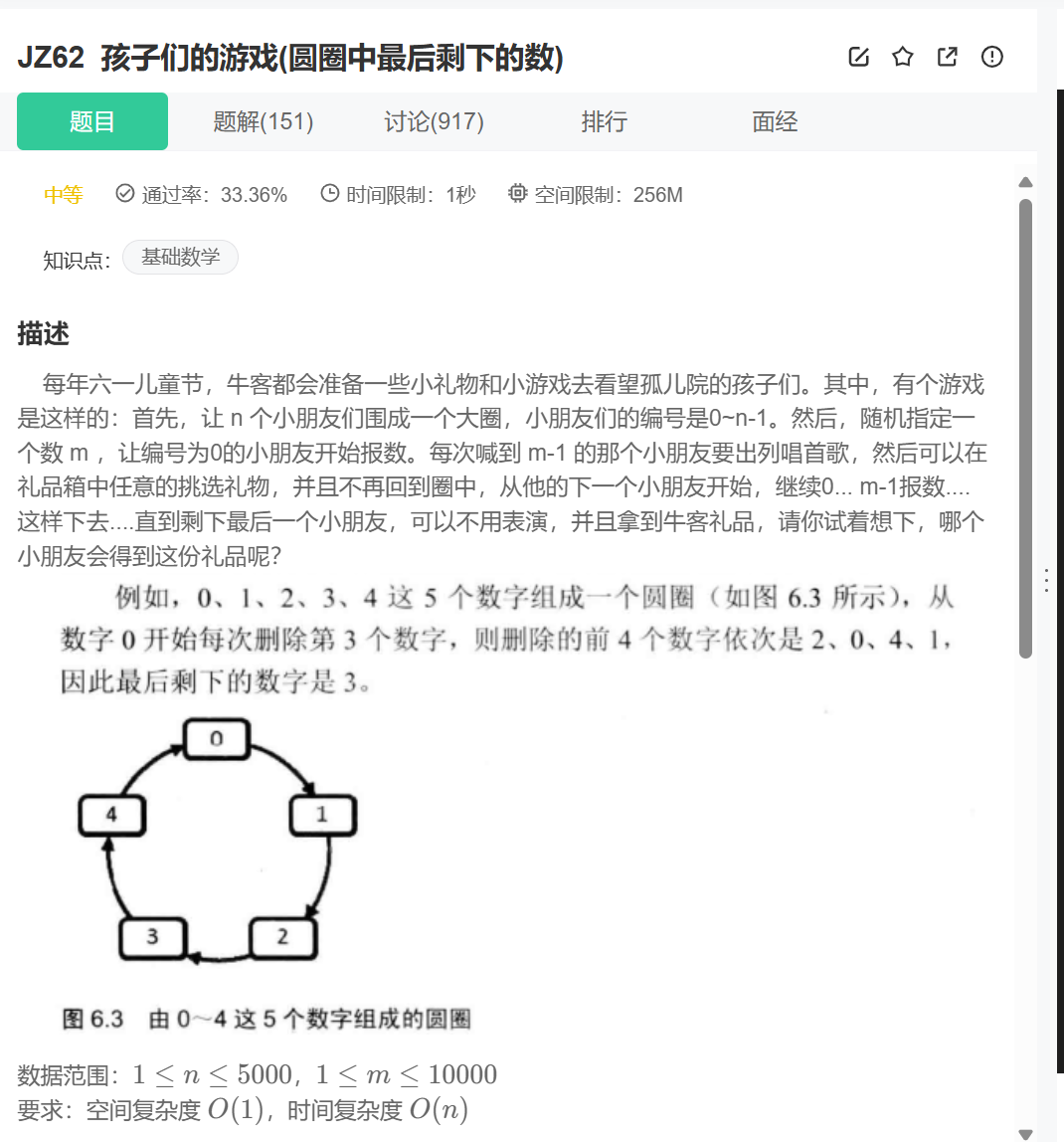
题目很好理解。就是一个约瑟夫环的问题。

74.2 算法思路

那么解决约瑟夫环的问题有很多种：

解法一就是：模拟

1.使用链表进行模拟

2.使用数组进行模拟。

那么如何解决转圈的问题呢？只需要i%n即可。n为数组的大小，i为下标位置。比如i的下标为5的时候，本质上不就是5%5=0吗？不就是下标从0开始的吗？

解法二：

这个才是咱们的重磅解法，就是动态规划：

那么通过这个，咱们可以知道，状态表示：

dp[i]:当有i个孩子围成一圈的时候，最终获胜的孩子的编号。

那么根据状态转移的推导方法，咱们需要知道dp[i]等于什么

那么此时咱们就需要关注一下dp[i-1]，这个咱们可以表示第i-1个孩子围成一圈的时候，最终获胜的孩子的编号是多少。那么这个dp[i-1]该怎么到dp[i]呢？

由于，每次去掉一个孩子的时候，那么都是从下一个孩子开始数的编号，即数到m-1.那么这样的话，1+m-1,就等于m，也就是说，dp[i-1]+m，就是当去掉获胜前一个孩子的时候，这个孩子距离获胜孩子的距离就是m。而又因为，咱们得考虑到转圈的问题，所以说，咱们的状态转移方程就出来了！

dp[i]=(dp[i-1]+m)%n

好，那么接下来，咱们就可以去做题目了。

74.3 代码演示：

//解法二：dp[n]=(dp[n-1]+m)%i
int LastRemaining_Solution(int n, int m)
{int f = 0;//这个地方只是起到了循环的作用，即重复多次，并不涉及变量的使用for (int i = 2; i <= n; i++) f = (f + m) % i;return f;
}
int main()
{int n, m;cin >> n >> m;cout << LastRemaining_Solution(n, m);return 0;
}

75 牛客网 简写单词

75.1 题目解析：

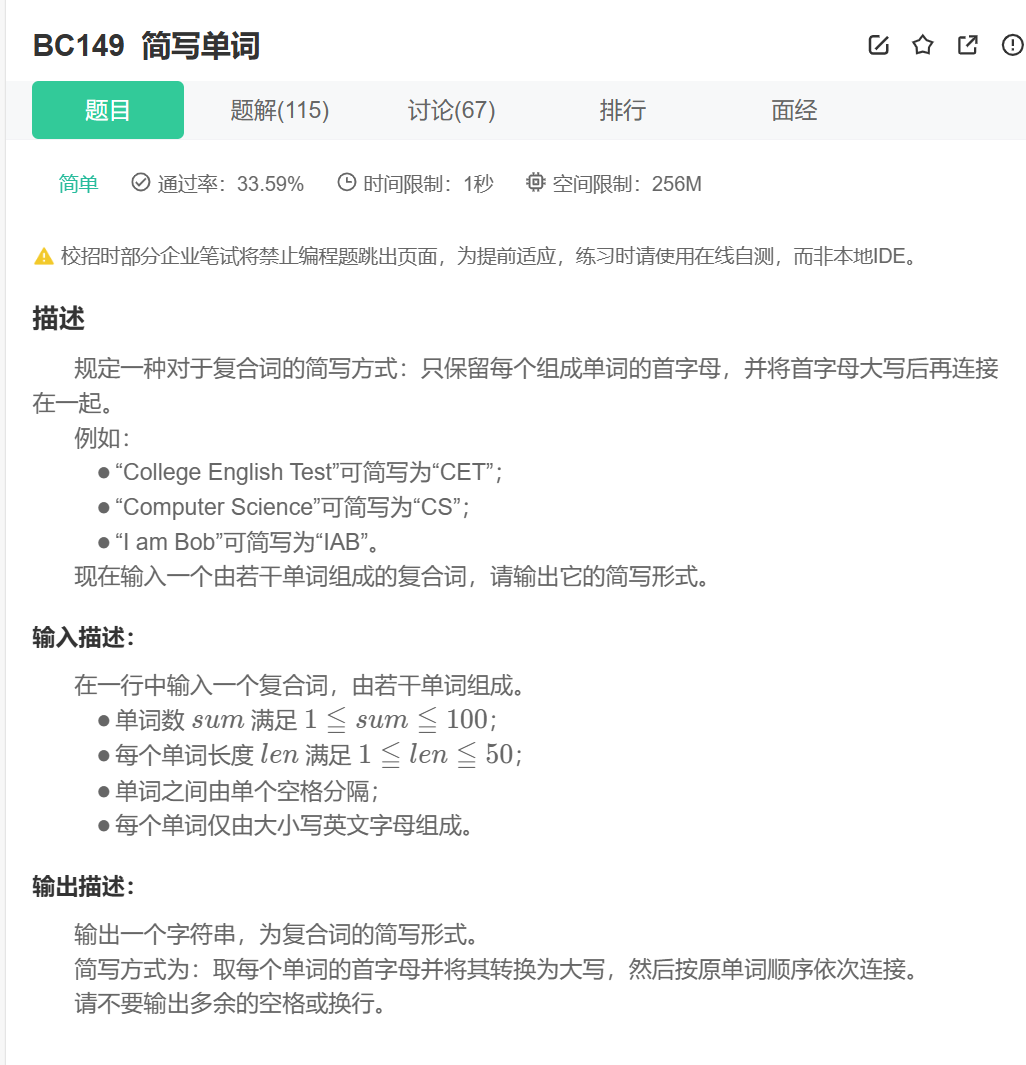
这个题目很好理解吧

75.2 算法思路

那么作者使用的做法就是，采用迭代器，由于第一个字母肯定是首字母，所以先记录下第一个字母。之后，遍历整个单词，找出空格，然后将空格之后的字母（肯定是首字母），记录下来。然后将记录的单词，全部转换成大写字母就大功告成了！

75.3 代码演示：

//牛客网简写单词
int main() {string outcome;string sentence;getline(cin, sentence);for (string::iterator it = sentence.begin(); it != sentence.end(); ++it){if (it == sentence.begin()){outcome += *it;}if (*it == ' '){outcome += *(it + 1);}}for (int i = 0; i < outcome.length(); i++){outcome[i] = toupper(outcome[i]);}cout << outcome << endl;}

76 牛客网 除2

76.1 题目解析：

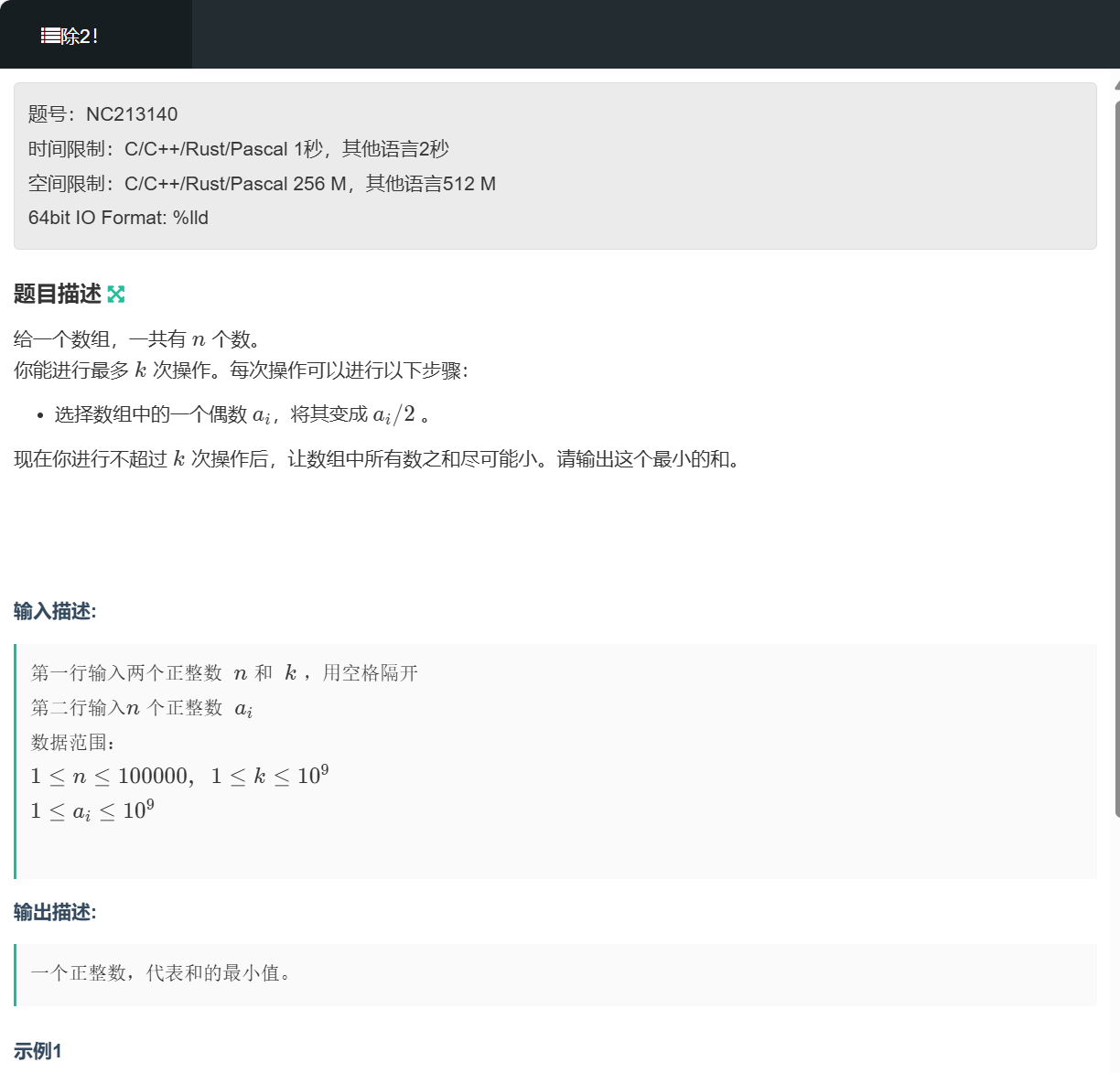
好，那么咱们直接来看算法思路

76.2 算法思路：

那么咱们需要怎么做呢？通过观察题目，咱们可以发现，只需要将最大的偶数除以2，每次都将最大的偶数除以2不就可以了吗?对，就是这么简单，但是这样的话，还涉及到一个问题，就是咱们不需要再总的输入，然后再总的输出了。咱们可以边输入，先计算出总和。然后让偶数进入大堆。进入里面之后，在大堆里面腰斩偶数即可。

76.3 代码演示

//正确代码
#include <iostream>
#include <queue>
using namespace std;
typedef long long LL;
LL n, k;
priority_queue<LL> heap;
int main()
{cin >> n >> k;LL sum = 0, x;while (n--){cin >> x;sum += x;if (x % 2 == 0) heap.push(x);}while (heap.size() && k--){LL t = heap.top() / 2; heap.pop(); sum -= t; if (t % 2 == 0) heap.push(t);}cout << sum << endl;return 0;
}

来看看作者一开始写的错误的代码：

typedef long long LL;
//通过率百分之50，但是我这个题目就不应该再把所有数字输进来之后，再进行堆排序了，而是直接进行在
//输入的时候就先加一下，然后加完之后，把偶数放入优先级队列，之后再对只有偶数的优先级队列进行
//操作，选出最大的数字啥的
int main() {LL outcome = 0;LL n = 0, k = 0;cin >> n >> k;priority_queue<int> pq;for (int i = 0; i < n; i++) {int num;cin >> num;pq.push(num);}while (k > 0) {int current = pq.top();pq.pop();if (current % 2 == 0) {pq.push(current / 2);k--;}else {outcome += current;continue;}}while (!pq.empty()) {outcome += pq.top();pq.pop();}cout << outcome << endl;return 0;
}

为什么错误呢？因为只通过了一半，另外一半由于超时了。这个超时的原因就是上面我说的那个原因。

77 牛客网 Fibonacci数列

77.1 题目解析：

题目也挺好理解的

77.2 算法思路：

咱们得先根据递推公式创造出这个数列。然后呢，咱们根据输入的数字对吧，看看距离这个数列中的哪个数更近，算出距离就可以了。还是很简单的一道模拟题目

77.3 代码演示：

typedef long long LL;
int main() {LL n = 0;cin >> n;vector<LL> nums(50, 0);nums[0] = 0;nums[1] = 1;//先创造出这个数列for (LL i = 2; i < nums.size(); i++) {nums[i] = nums[i - 1] + nums[i - 2];}//之后让输出的数字判断在哪个区间里面，然后找出距离最小的for (LL j = 0; j < nums.size(); j++) {if (n<nums[j + 1] && n>nums[j]) {cout << min(n - nums[j], nums[j + 1] - n) << endl;break;}else if (n == nums[j]) {cout << 0 << endl;break;}}return 0;
}

78 牛客网 游游的you

78.1 题目解析：

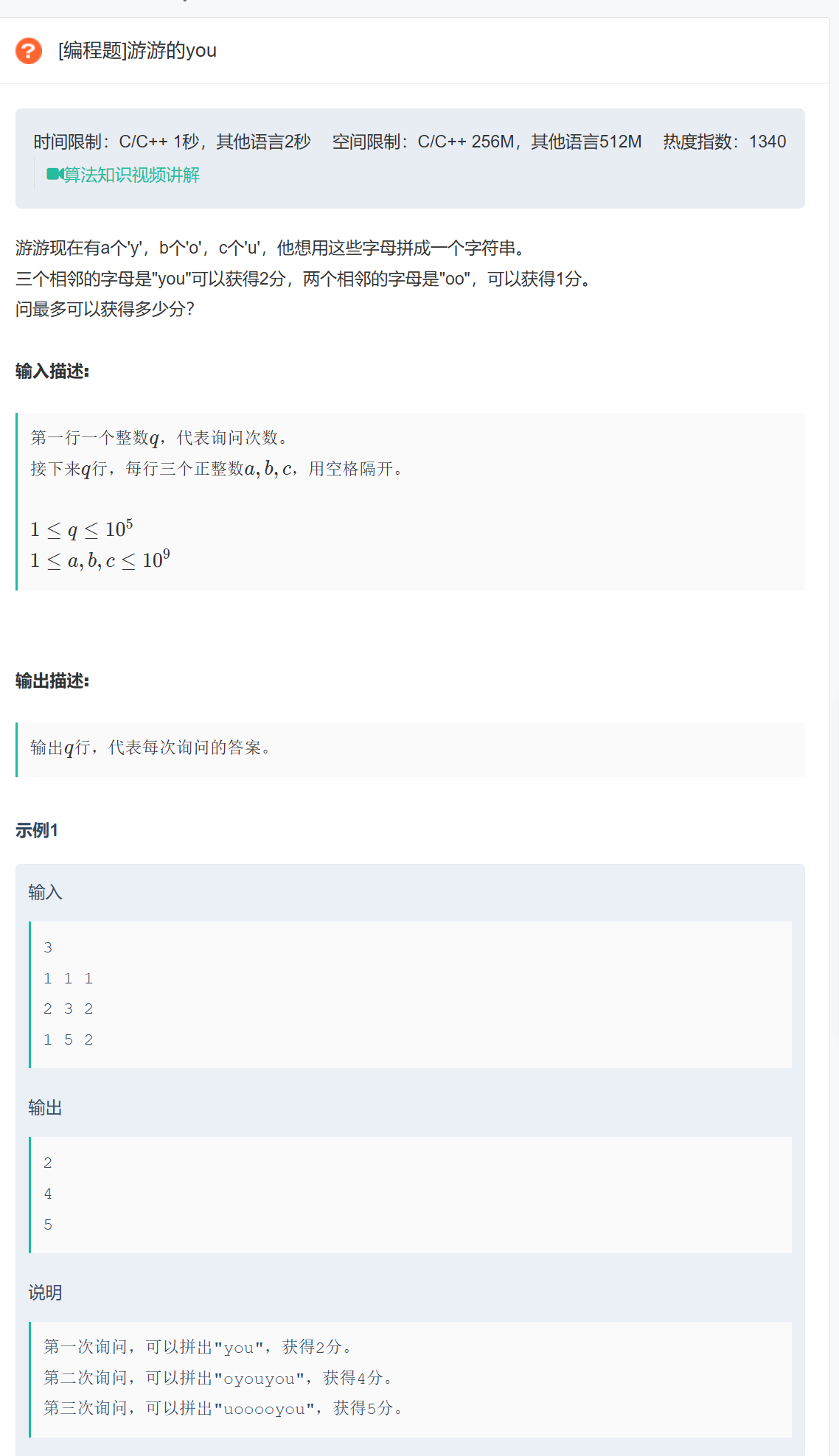
这道题目也是一道简单题目，

78.2 算法思路：

通过观察就可以看出来。这个其实可以分为两大类：

1.就是如果说a，b，c都是大于等于1的，说明，可以凑出一个you

2.如果说，单独的b大于等于2，说明可以拿到b-1的分数的

那么接下来看代码

78.3 代码演示：

int main() {int q;cin >> q;int a, b, c;vector<int> nums;//输出的时候用while (q > 0){ int score = 0;cin >>a >>b >>c;q--;while (a >= 1 && b >= 1 && c >= 1){score += 2;a--;b--;c--;}while (b >= 2){score += b - 1;break;}nums.push_back(score);}for (int i = 0; i < nums.size(); i++){cout << nums[i] << endl;}
}

欧克，本篇文章可算是讲完了......