【系统架构设计（38）】数据库规范化理论

一、概述

数据库规范化理论是关系型数据库设计的核心理论基础，旨在通过消除数据冗余、更新异常、插入异常和删除异常等问题，设计出结构合理、性能优良的数据库模式。规范化理论通过一系列范式（Normal Form）来指导数据库设计，从第一范式到BC范式，逐步消除不同类型的函数依赖关系，最终实现数据库结构的最优化。

二、非规范化存在的问题

问题类型	表现	具体示例	主要危害
数据冗余	同一信息在多个记录中重复存储	计算机系的"D01"、“计算机系”、"1号楼"在多个学生记录中重复出现	• 占用过多存储资源，增加存储成本 • 数据维护难度增大，容易出现数据不一致 • 影响数据库的存储效率和查询性能
更新异常	修改信息时必须同时修改所有相关记录	计算机系位置变化时，需逐一修改所有该系学生记录中的"系位置"字段	• 破坏数据的完整性和一致性 • 影响数据的准确性 • 可能导致决策偏差 • 增加数据维护的复杂性和出错概率
插入异常	某些情况下无法插入需要的数据	新增系信息时，若该系还没有学生记录，就无法插入系的"系号"、“系名”、"系位置"等信息	• 无法及时准确地录入新的系信息 • 影响数据库对现实情况的准确反映 • 阻碍业务正常开展 • 限制数据库的扩展性
删除异常	删除记录时可能意外删除其他重要信息	删除S01学生记录时，若该系只有这一条记录，会同时删除系的"系号"、“系名”、"系位置"等信息	• 造成数据丢失 • 破坏数据库中数据的完整性 • 影响后续对系相关信息的查询和使用 • 可能导致业务逻辑错误

总结：非规范化的关系模式存在诸多问题，通过关系模式的规范化（如满足范式要求）可以有效解决这些问题。

 

三、规范化理论基本概念

3.1 函数依赖

函数依赖是关系数据库中描述属性间逻辑关系的核心概念。

给定关系模式$R(U,F)$，其中$U$是属性集合，$F$是函数依赖集合。$X$和$Y$是$U$的子集，$r$是关系模式$R$对应的关系（即一张具体的表）。对于$r$中的任意两个元组（表中的行）$u$和$v$，当元组在属性集$X$上的值相等时（$u[X]=v[X]$），在属性集$Y$上的值也必然相等（$u[Y]=v[Y]$），就称$X$函数决定$Y$，或者说$Y$函数依赖于$X$，记作$X\to Y$。

这种依赖关系体现了数据间的确定性联系：一旦$X$的值确定，$Y$的值就唯一确定。这意味着在关系模式中，$X$作为决定因素，能够完全决定$Y$的取值，不存在$X$相同但$Y$不同的情况。

函数依赖是数据库规范化理论的基础，直接影响数据库设计的质量和性能。

在数据库设计过程中，函数依赖分析帮助识别数据冗余和异常问题。例如，当发现"学号→系名"这样的传递依赖时，设计者能够意识到需要将学生信息和系信息分离，避免在每一条学生记录中重复存储系名信息。

 

3.2 键

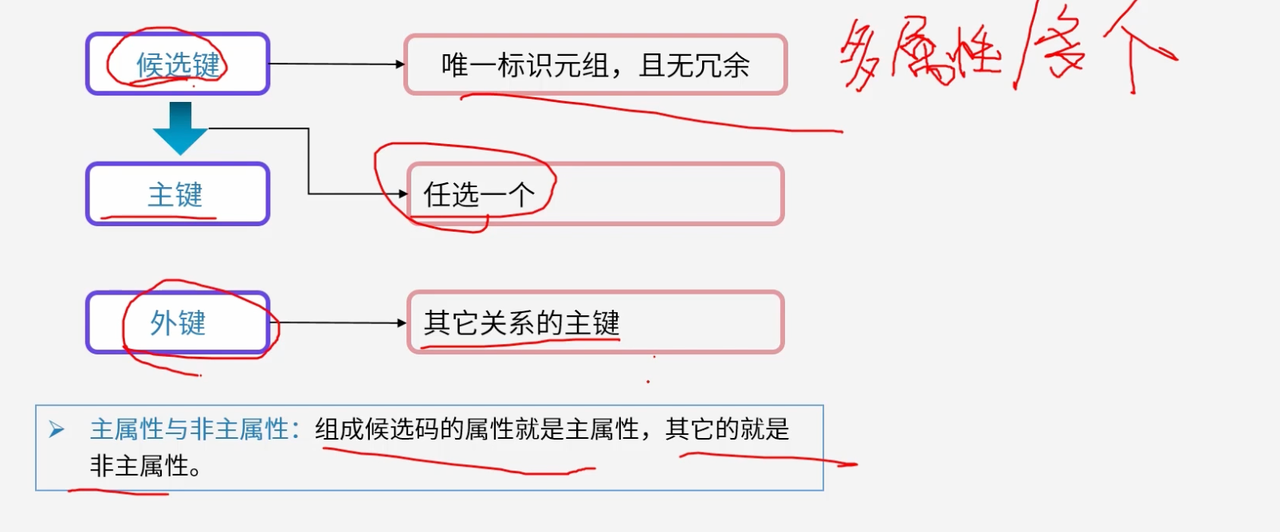
3.2.1 候选键：唯一标识的基础

候选键是关系模式中能够唯一标识每个元组的最小属性集合。

在"学生（学号，姓名，年龄，班级编号）"关系中，学号能够唯一标识每个学生，因此学号就是一个候选键。候选键必须具有唯一性和最小性，确保每个元组都有明确的身份标识。

3.2.2 主键：关系模式的核心标识

主键是从候选键中选择的一个，承担着关系模式的核心标识职责。

主键是建立表间关联的基础，是数据完整性约束的核心，也是数据库操作的主要依据。主键的选择直接影响整个数据库系统的性能和可维护性。

3.2.3 外键：关系间的桥梁

外键是建立不同关系之间联系的桥梁，实现了数据的关联和参照完整性。

在"学生"关系中的"班级编号"字段，如果它是"班级"关系的主键，那么"班级编号"就是"学生"关系的外键。外键保证了参照完整性，防止数据不一致问题的发生。

3.2.4 主属性与非主属性：属性的分类管理

根据属性在候选键中的作用，可以将关系模式中的属性分为主属性和非主属性两大类。

主属性是组成候选键的属性，非主属性则是除主属性之外的其他属性。在规范化过程中，非主属性对候选键的依赖关系是判断范式等级的关键依据。

 

3.3 候选键的寻找（基于图示法）

3.3 候选键的寻找方法

通过构建函数依赖有向图来寻找候选键，是系统化分析关系模式的有效方法。

首先将每个属性表示为图中的节点，函数依赖关系表示为有向边。然后识别入度为0的属性（不依赖于任何其他属性的属性），这些属性是候选键的关键起点。最后通过遍历分析确定完整的候选键：如果入度为0的属性集合能够遍历图中所有节点，则构成候选键；否则需要将中间节点并入候选键集合，确保能够遍历所有节点。这种方法通过系统性的图遍历，确保找到的属性集合既能唯一标识所有元组，又具有最小性。

 

3.4 函数依赖类型

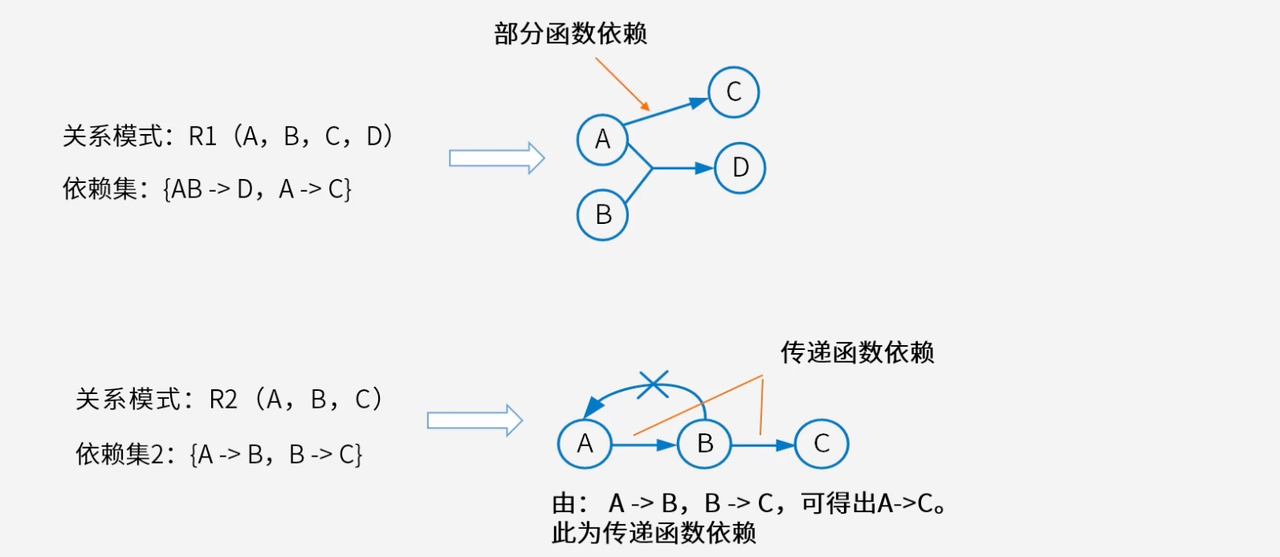
3.4.1 部分函数依赖：冗余决定因素的问题

部分函数依赖是指决定因素中存在冗余属性，其中一部分属性就能决定被决定因素。

在关系模式$R1(A,B,C,D)$中，如果存在依赖集{AB→D,A→C}\{AB \to D, A \to C\}{AB→D,A→C}，那么对于$A\to C$这个依赖关系，$C$实际上只依赖于$AB$中的$A$部分，而不需要$B$的参与。这种依赖关系表明$AB$作为决定因素存在冗余。

部分函数依赖的存在往往意味着关系模式设计不够优化。当候选键是复合属性时，如果非主属性只依赖于候选键的一部分，就会导致数据冗余和更新异常。因此，在规范化过程中，识别和消除部分函数依赖是提高数据库设计质量的关键步骤。

3.4.2 传递函数依赖：间接依赖的复杂性

传递函数依赖通过中间属性建立间接的依赖关系，增加了数据管理的复杂性。

在关系模式$R2(A,B,C)$中，如果存在依赖集{A→B,B→C}\{A \to B, B \to C\}{A→B,B→C}，那么可以推导出$A\to C$，这里$C$对$A$就是传递函数依赖。$C$不是直接依赖于$A$，而是通过中间属性$B$间接依赖于$A$。

传递函数依赖虽然逻辑上成立，但在实际应用中会带来诸多问题。当需要更新$C$的值时，必须同时考虑$A$和$B$的变化；当删除包含$B$的记录时，可能会意外丢失$C$的信息。因此，在数据库设计中，通常需要通过关系模式分解来消除传递函数依赖，使每个关系模式中的依赖关系更加直接和清晰。

 

3.5 公理系统

3.5.1 Armstrong公理：函数依赖推理的基础

Armstrong公理为函数依赖的推理提供了严格的数学基础，是规范化理论的核心工具。

自反律（A1） 体现了属性集合的包含关系：如果$Y$是$X$的子集，那么$X$必然能够决定$Y$。在关系模式$R(A,B,C)$中，由于{A}\{A\}{A}是{A,B}\{A, B\}{A,B}的子集，所以$A,B\to A$必然成立。这个公理反映了"整体决定部分"的基本逻辑。

增广律（A2） 说明了函数依赖的扩展性：在决定因素和被决定因素两边同时增加相同属性集，依赖关系依然成立。如果$A\to B$成立，那么$AC\to BC$也必然成立，这为复合属性的依赖关系分析提供了依据。

传递律（A3） 揭示了函数依赖的传递性：如果$A\to B$且$B\to C$，那么$A\to C$也成立。这个公理是识别传递函数依赖的理论基础，也是规范化过程中需要消除的依赖类型。

3.5.2 导出推理规则：公理系统的扩展

基于Armstrong公理，我们可以推导出更多实用的推理规则，这些规则大大简化了函数依赖的分析过程。

合并规则 允许我们将多个具有相同决定因素的依赖关系合并：如果$A\to B$且$A\to C$，那么$A\to BC$。这个规则在分析复合属性依赖时特别有用，能够将多个简单的依赖关系整合为一个复合依赖关系。

伪传递规则 处理了更复杂的传递情况：如果$A\to B$且$BC\to D$，那么$AC\to D$。这个规则在分析涉及多个属性的传递依赖时非常实用，能够识别出通过复合属性建立的间接依赖关系。

分解规则 与合并规则相反，允许我们将复合依赖关系分解为简单的依赖关系：如果$A\to BC$，那么$A\to B$和$A\to C$都成立。这个规则在识别部分函数依赖时具有重要作用。

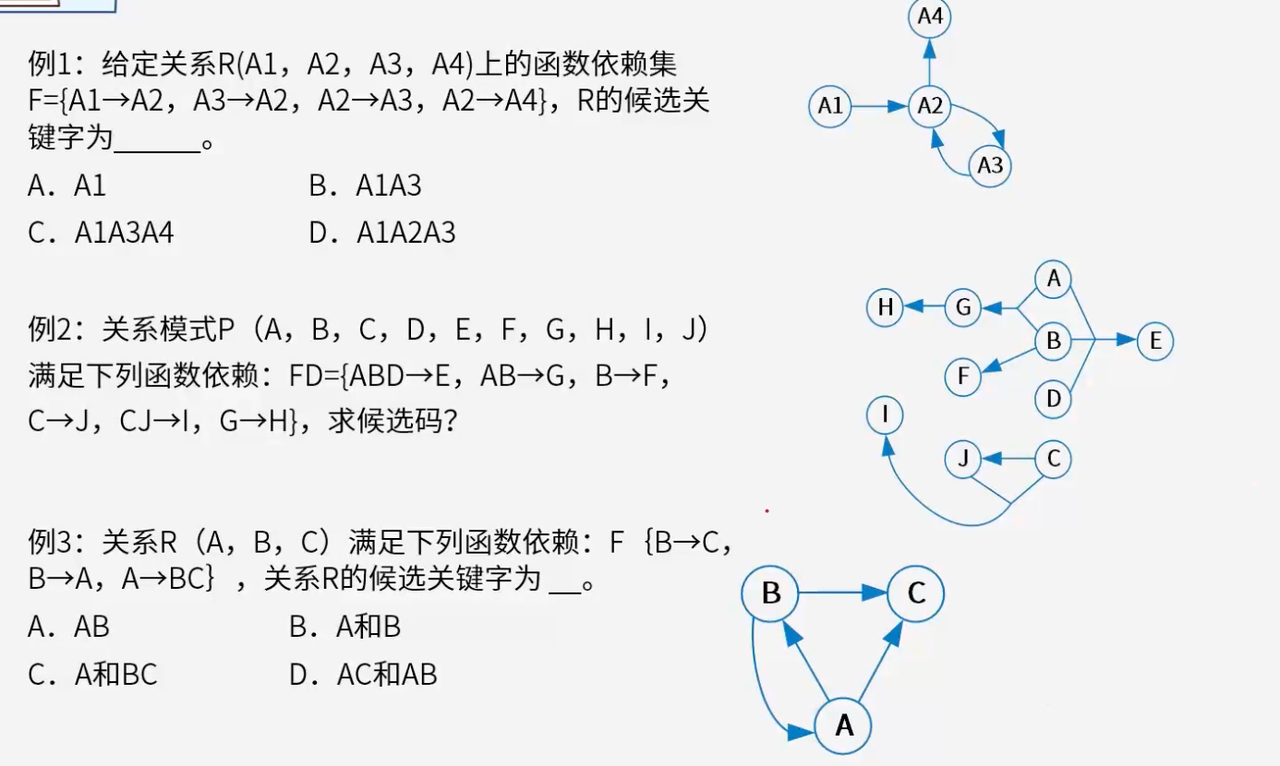
• 由A1可以找到所有节点
• ABCD组合作为候选码
• B

 

四、范式判断

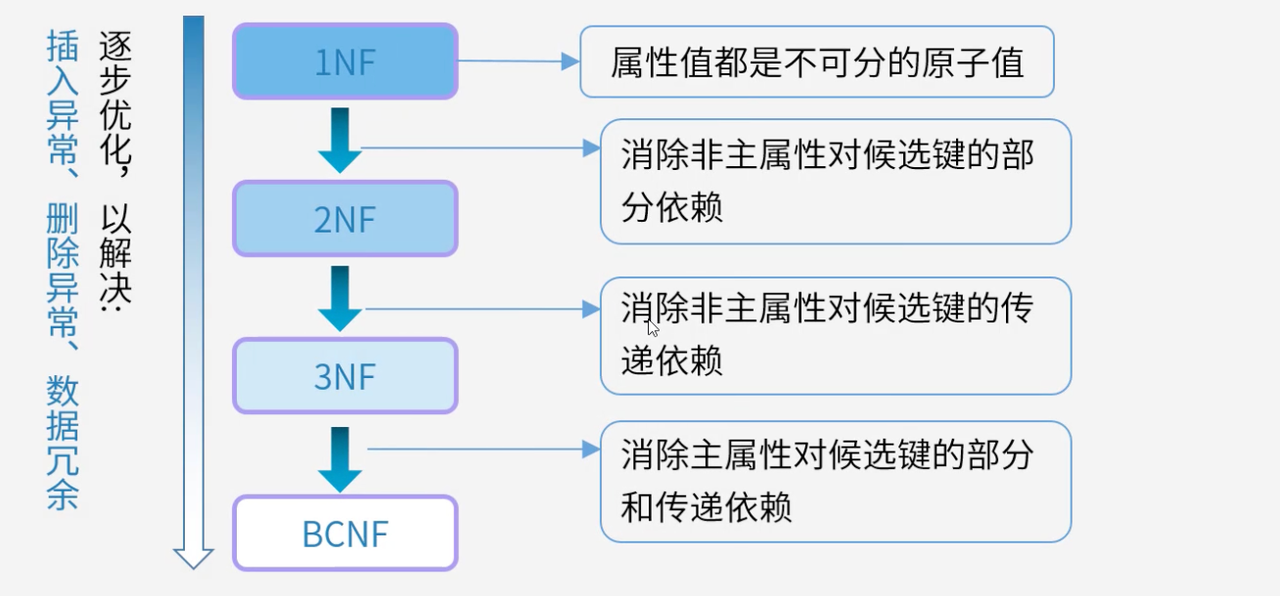
4.1 范式概述

范式是关系模式规范化的标准，从第一范式到BC范式，逐步消除不同类型的函数依赖关系，最终实现数据库结构的最优化。

4.2 第一范式（1NF）

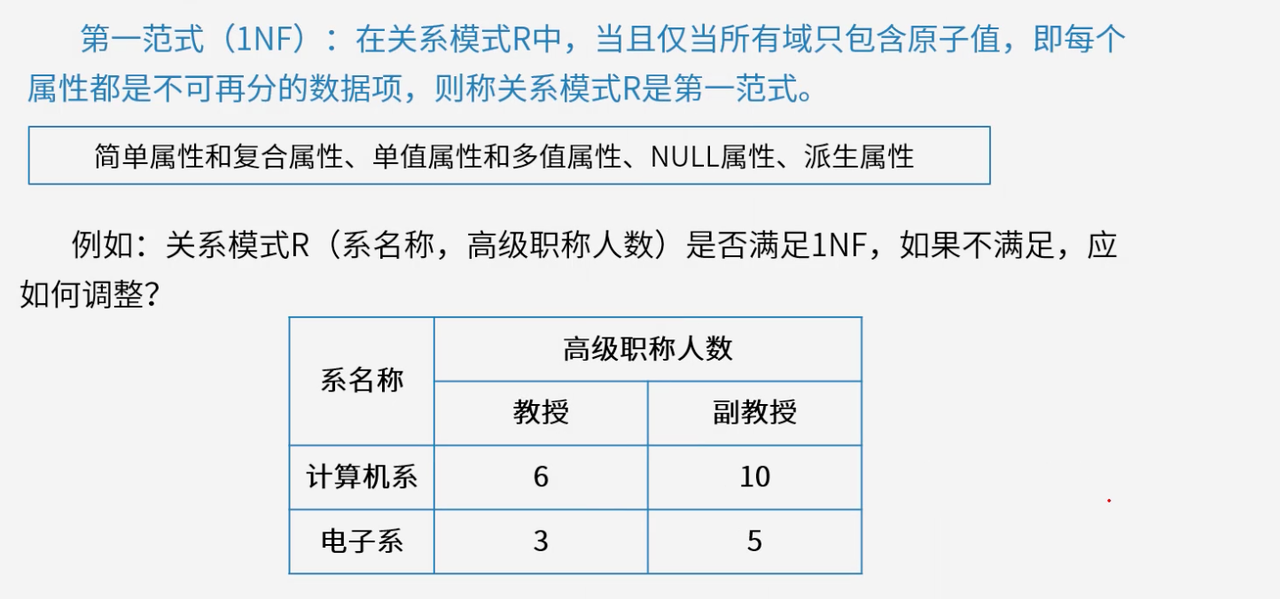
第一范式要求关系模式中的属性值都是不可再分的原子值，是关系数据库规范化的基础。

关系模式中的每个字段都应该是单一的值，不能包含重复组或子结构。例如在"学生"表中，"姓名"字段不能同时存储多个姓名，"成绩"字段不能是成绩的集合。

属性类型处理：简单属性（如"姓名"）直接满足1NF；复合属性（如"地址"）需分解为简单属性（“省”、“市”、“区”）；多值属性（如"爱好"）需拆分成多个记录；派生属性（如"年龄"）一般不单独存储。

示例分析：关系模式R（系名称，高级职称人数）不满足1NF，因为"高级职称人数"被细分为"教授"和"副教授"两个子属性。调整方法有两种：一是拆分成两个关系模式R1（系名称，教授人数）和R2（系名称，副教授人数）；二是合并为"高级职称总人数"属性，使关系模式满足1NF。

 

4.3 第二范式（2NF）

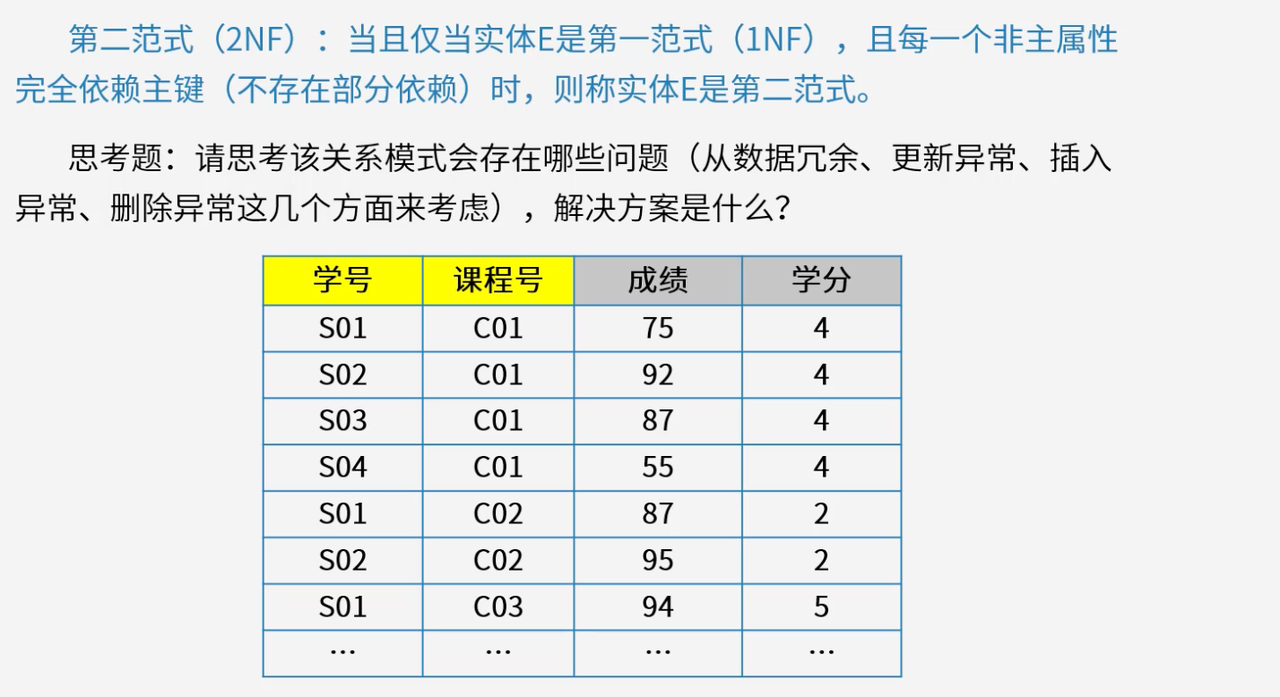
第二范式在满足1NF的基础上，消除非主属性对候选键的部分依赖，要求非主属性完全依赖于候选键。

在关系模式$R(A,B,C,D)$中，若候选键是$AB$，且存在$A\to C$这种部分依赖情况，就不满足2NF。2NF进一步优化关系模式，减少数据冗余，降低插入、删除异常发生的可能性。

问题分析：部分依赖会导致数据冗余、更新异常、插入异常和删除异常。例如同一门课程的学分在多条记录中重复出现，学分调整时需要修改所有相关记录，新增课程时无法插入信息，删除学生选课记录时会丢失课程信息。

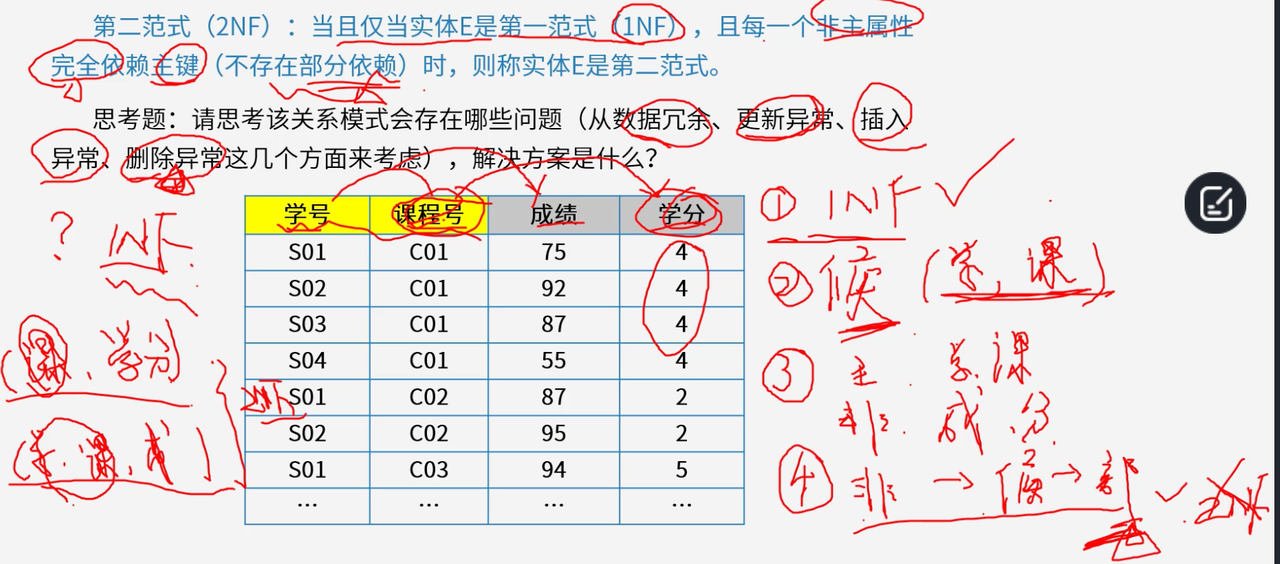
解决方案：将原关系模式分解为两个关系模式。以选课关系为例，分解为"选课（学号，课程号，成绩）"和"课程（课程号，学分）"两个关系模式。这样分解后，每个关系模式中的非主属性都完全依赖主键，满足2NF，消除了各种异常问题。

 

4.4 第三范式（3NF）

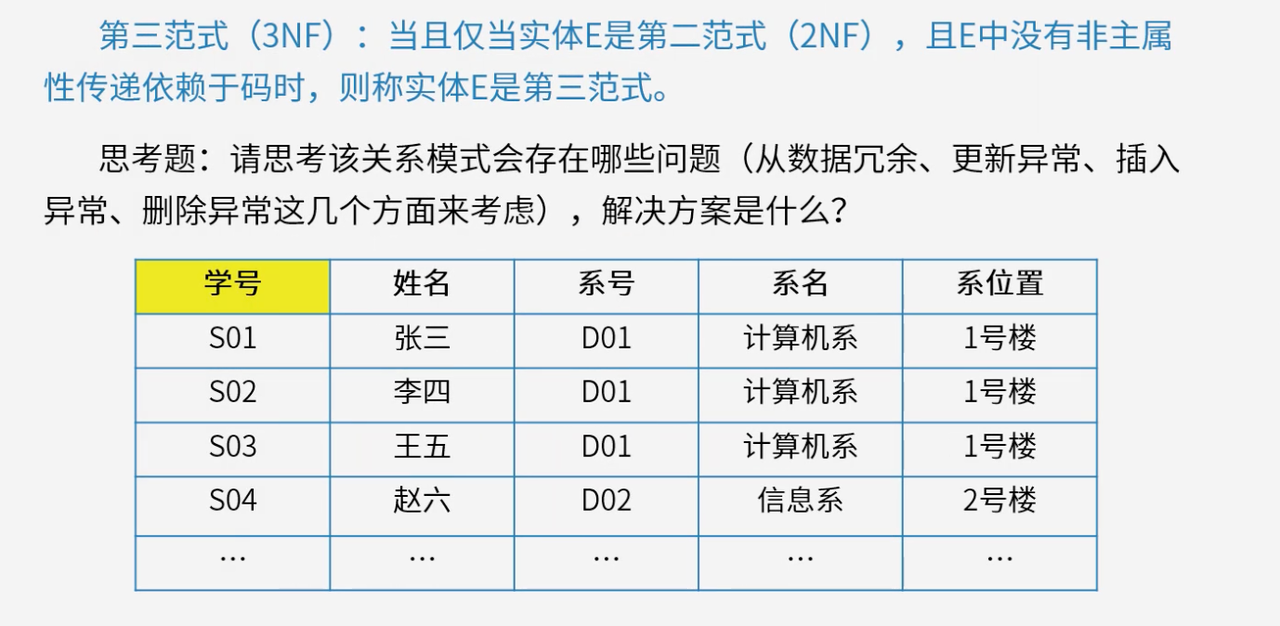
第三范式在满足2NF的基础上，消除非主属性对候选键的传递依赖。

如果关系模式中存在$X\to Y$，$Y\to Z$（$Y$不依赖于$X$，$Z$不依赖于$Y$），且$X$是候选键，$Z$是非主属性，就存在传递依赖，不满足3NF。3NF使关系模式更合理，数据冗余进一步降低，数据的完整性和一致性更易维护。

 

4.5 巴斯-科德范式（BCNF）

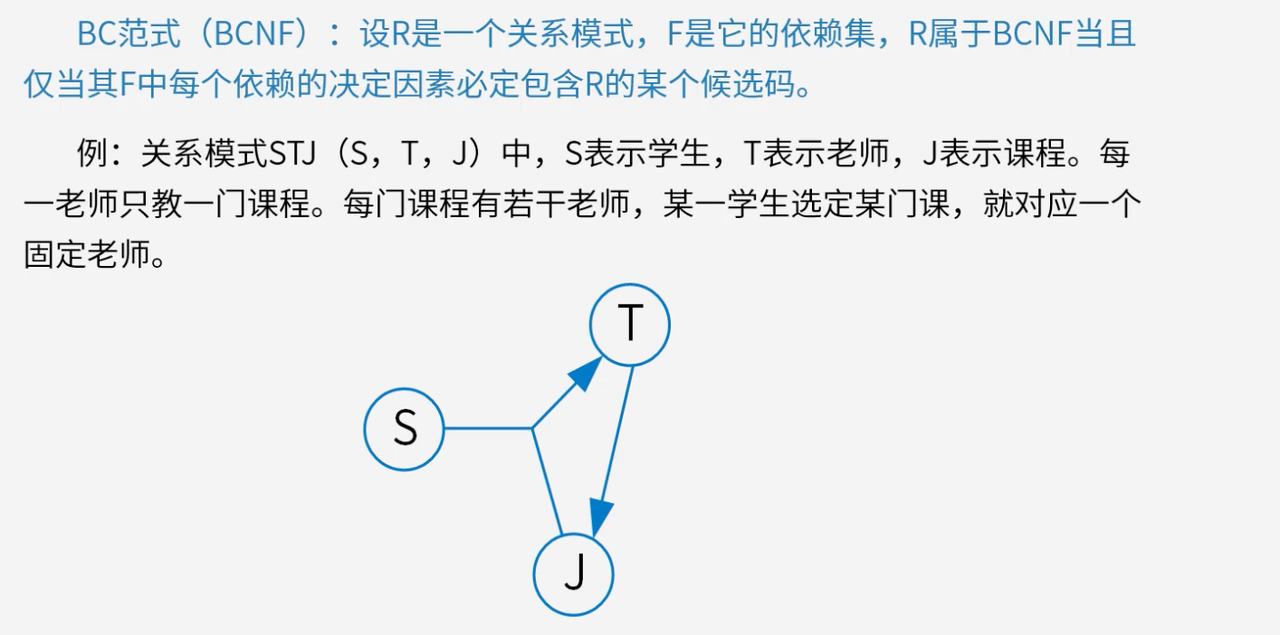
BCNF在满足3NF的基础上，消除主属性对候选键的部分和传递依赖，是关系模式规范化的更高标准。

对于关系模式中的每一个非平凡函数依赖$X\to Y$（$Y$不是$X$的子集），$X$都必须是候选键。BCNF能最大程度地减少数据冗余和操作异常，提高数据库的性能和数据质量。

判断过程：以关系模式$STJ(S,T,J)$为例，存在函数依赖$T\to J$和$(S,J)\to T$，候选码是$(S,J)$和$(S,T)$。对于函数依赖$T\to J$，决定因素$T$不是候选码，不满足BCNF要求。解决方案是将$STJ$分解为$ST(S,T)$和$TJ(T,J)$两个关系模式，每个都满足BCNF。

这几种范式层层递进，通过逐步消除不同类型的函数依赖，优化关系模式，解决插入异常、删除异常和数据冗余等问题。

 

五、模式分解

5.1 保持函数依赖分解

保持函数依赖分解是关系模式分解中的重要概念，确保分解后的子模式函数依赖集与原关系模式在逻辑上等价。

当把关系模式$R$分解成多个子模式ρ={R1,R2,⋯,Rk}\rho = \{R1, R2, \cdots, Rk\}ρ={R1,R2,⋯,Rk}时，如果这些子模式的函数依赖集{F1,F2,⋯,Fk}\{F1, F2, \cdots, Fk\}{F1,F2,⋯,Fk}与原关系模式的函数依赖集$F$能相互逻辑蕴涵，就称这种分解$\rho$保持了函数依赖。

示例说明：关系模式$R(A,B,C)$，函数依赖集F={A→B,B→C}F = \{A \to B, B \to C\}F={A→B,B→C}，分解为ρ={R1(A,B),R2(B,C)}\rho = \{R1(A, B), R2(B, C)\}ρ={R1(A,B),R2(B,C)}。$R1$的函数依赖集F1={A→B}F1 = \{A \to B\}F1={A→B}，$R2$的函数依赖集F2={B→C}F2 = \{B \to C\}F2={B→C}。{F1,F2}\{F1, F2\}{F1,F2}与$F$等价，因为可以通过传递律得到$A\to C$等依赖关系，所以这种分解是保持函数依赖的。

重要性：保持函数依赖分解确保数据完整性，维护原有的函数依赖关系，保证数据之间的逻辑关系不会出现混乱。同时有助于保证分解后的关系模式在进行数据操作时能够正确反映业务规则，提高数据库设计的质量和可用性。

5.2 无损分解判断

5.2.1 无损分解概念

概念理解：

• 有损分解：当对一个关系模式进行分解后，无法通过自然连接、投影等运算还原出原始的关系模式，意味着在分解过程中丢失了部分信息，这种分解就是有损分解。比如在分解过程中，某些元组间的关联信息被破坏且无法恢复。

• 无损分解：将一个关系模式分解成若干个关系模式后，利用自然连接和投影等运算能够完整地还原到原来的关系模式，即分解过程没有丢失任何信息。这是关系模式分解中期望达到的重要特性。

无损联接分解要点：

• 分解后的还原操作：通过自然连接和投影等运算来实现还原。自然连接是在两个关系中，基于相同属性列进行连接，并去掉重复列；投影是选择关系中的若干属性列组成新的关系。例如关系模式$R(A,B,C)$分解为$R1(A,B)$和$R2(B,C)$，若能通过对$R1$和$R2$进行自然连接操作，得到与$R$完全相同的关系模式，就说明是无损联接分解。

• 重要性：无损分解保证了在对关系模式进行规范化等分解操作时，数据的完整性得以保留。如果是有损分解，后续基于分解后的关系模式进行的数据查询、更新等操作可能会得到不准确或不完整的结果，影响数据库的正确性和可用性。

5.2.2 用表格法分析无损分解

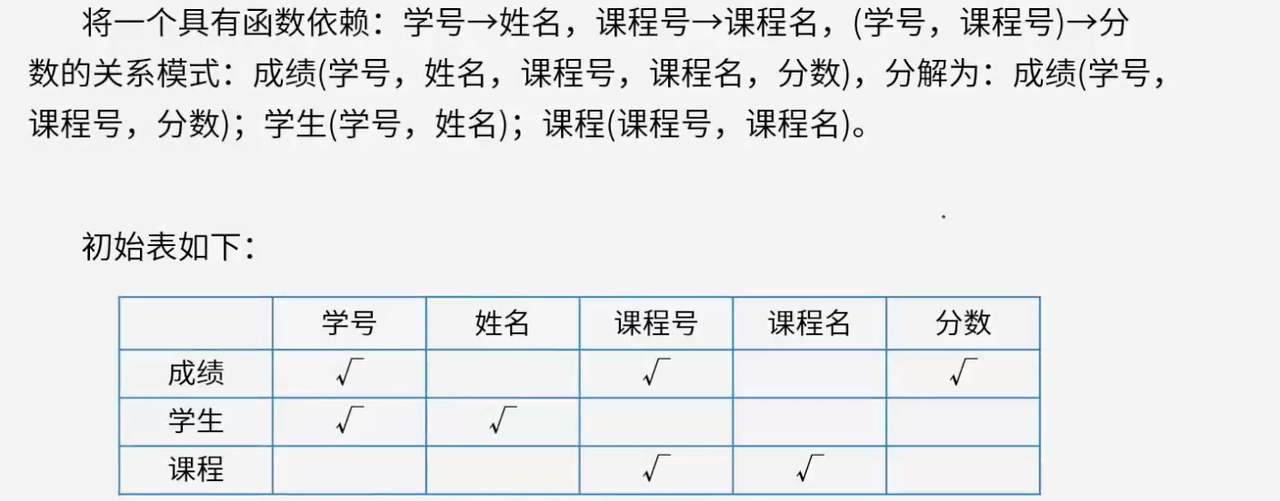
5.2 无损分解判定

通过表格判定法来确定关系模式分解是否为无损分解，其核心思路是根据给定的函数依赖关系，逐步对表格中的元素进行标记。

步骤分析：

• 初始标记：根据关系模式的分解情况，对每个关系模式所涉及的属性列进行标记。如"成绩"关系模式涉及学号、课程号、分数，就在对应列标记√；"学生"关系模式涉及学号、姓名，就在对应列标记√，其余列标记×。

• 依据函数依赖修正标记：依据"学号→姓名"，由于"学生"关系模式中已有学号对应姓名的依赖关系体现，所以将"成绩"关系模式中姓名列的×改为√。依据"课程号→课程名"，由于"课程"关系模式中已有课程号对应课程名的依赖关系体现，所以将"成绩"关系模式中课程名列的×改为√。

• 判断结果：经过上述操作后，如果某个关系模式所在行所有属性列均为√，则说明能通过这些分解后的关系模式还原出原始关系模式，即该分解是无损分解。

这种方法直观地利用表格和函数依赖关系判断分解是否无损，在数据库关系模式分解判定中较为常用。

 

5.2.3 公式法

无损联接分解定理为判断关系模式分解是否无损提供了明确的规则。

对于关系模式$R$分解为ρ={R1,R2}\rho = \{R_1, R_2\}ρ={R1​,R2​}，判断其是否为无损联接分解，依据是看$R_1\cap R_2$（公共属性）能否函数决定$R_1-R_2$（$R_1$去掉公共属性后的属性集）或者$R_2-R_1$（$R_2$去掉公共属性后的属性集）。若能满足其中之一，分解就具有无损联接性，即通过自然连接等运算可还原原始关系模式。

示例分析：

• 分解ρ1={R1(AB),R2(AC)}\rho_1 = \{R_1(AB), R_2(AC)\}ρ1​={R1​(AB),R2​(AC)}：$R_1\cap R_2=A$，$R_1-R_2=B$，$R_2-R_1=C$。依据函数依赖集F={A→B}F = \{A \to B\}F={A→B}，存在$A\to B$，满足无损联接分解的充分必要条件，所以分解${\rho }_1$是无损分解。

• 分解ρ2={R1(AB),R3(BC)}\rho_2 = \{R_1(AB), R_3(BC)\}ρ2​={R1​(AB),R3​(BC)}：$R_1\cap R_3=B$，$R_1-R_3=A$，$R_3-R_1=C$。函数依赖集F={A→B}F = \{A \to B\}F={A→B}中不存在$B\to A$或$B\to C$，不满足无损联接分解的充分必要条件，所以分解${\rho }_2$不是无损分解。

这种判定方法有助于在数据库设计中合理分解关系模式，确保分解后的关系模式能够完整还原原始数据。

AD

 

六、总结

数据库规范化理论是关系型数据库设计的核心理论基础，通过系统化的方法解决非规范化关系模式中存在的各种问题。从数据冗余、更新异常、插入异常到删除异常，规范化理论提供了完整的解决方案。

函数依赖作为规范化理论的基础概念，通过Armstrong公理系统建立了完整的推理体系，为关系模式的优化提供了理论支撑。从第一范式到BC范式，逐步消除部分函数依赖和传递函数依赖，最终实现数据库结构的最优化。

模式分解作为规范化的重要手段，通过保持函数依赖和无损分解的判断方法，确保分解后的关系模式既能保持数据的完整性，又能维持原有的逻辑关系。表格法和公式法为无损分解的判断提供了实用的工具。

规范化理论不仅解决了数据库设计中的技术问题，更重要的是提供了一种系统性的设计思维。通过分层递进的范式要求，将复杂的数据库设计问题分解为可管理的步骤，最终实现高效、稳定、可维护的数据库系统。

因此，掌握数据库规范化理论不仅有助于设计出高质量的数据库，更重要的是培养了系统性的分析和设计能力，这种能力在解决复杂工程问题时具有重要价值。