二分查找思路详解，包含二分算法的变种，针对不同题的做法

👨‍💻程序员三明治：个人主页
🔥 个人专栏: 《设计模式精解》 《重学数据结构》

🤞先做到 再看见！

---

传统的解题思路

题目

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target，写一个函数搜索 nums 中的 target，如果目标值存在返回下标

思路

左闭右闭

class Solution {public int search(int[] nums, int target) {// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算if (target < nums[0] || target > nums[nums.length - 1]) {return -1;}int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target) {return mid;}else if (nums[mid] < target) {left = mid + 1;}else { // nums[mid] > targetright = mid - 1;}}// 未找到目标值return -1;}
}

左闭右开

class Solution {public int search(int[] nums, int target) {int left = 0, right = nums.length;while (left < right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target) {return mid;}else if (nums[mid] < target) {left = mid + 1;}else { // nums[mid] > targetright = mid;}}// 未找到目标值return -1;}
}

153寻找排序数组中的最小值

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

思路

理解题意

「旋转」的定义是：把一个数组最开始的若干个元素「搬」到数组的末尾，也可以「不搬」元素。

分析旋转数组的特点

• 多次旋转等价于旋转一次；
• 只会有一次「转折」，一分为二看，一定有一段是有序的；
• 重点理解 1：最大值和最小值相邻，即：最大值的右边，如果有的话，一定是最小值；
• 重点理解 2：如果两点是上升的，那么两点之间一定是上升的。

下面说明如果两点是上升的，那么两点之间一定是上升的。如图：

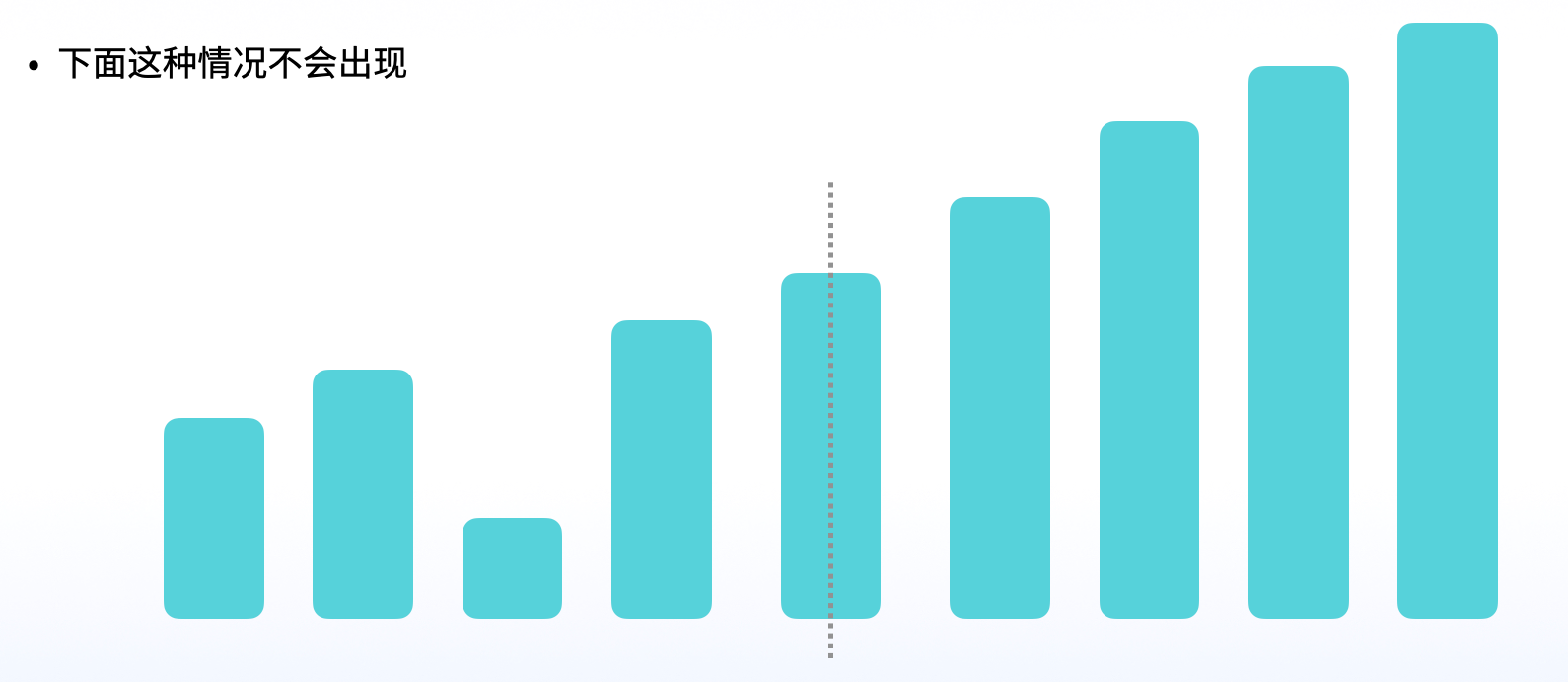
左边 < 中间，从左边到中间就一定是上升的，否则就不能称为是旋转有序数组。

在旋转有序数组上，有 3 个位置比较重要，它们分别是最左边元素、中间元素和最右边元素。

「比较最左边和中间」还是「比较中间和最右边」?

1. 比较左边和中间会发现，最小值可能在前面，也可能在后面

下图都满足最左边 < 中间，但是左图最小值在后面，右图最小值在前面。

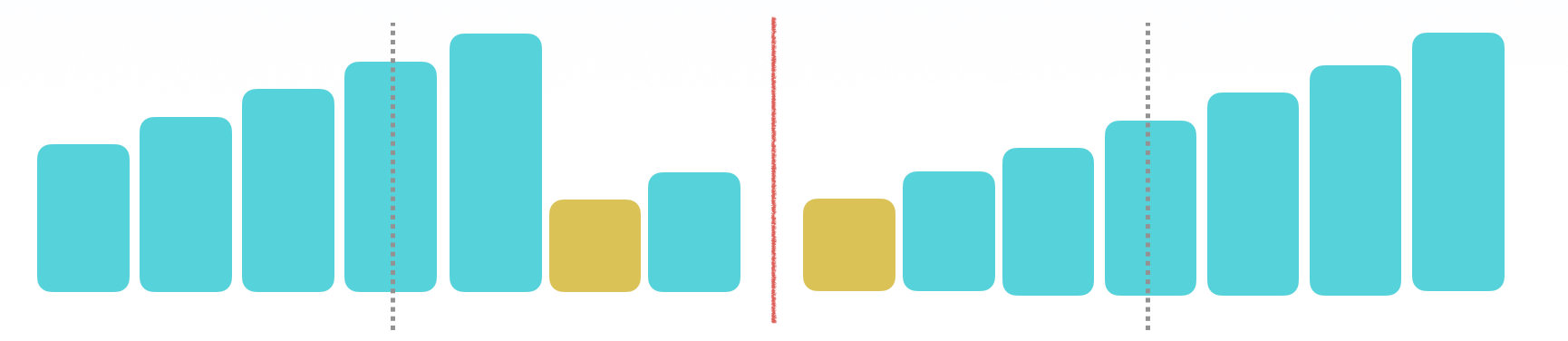
最极端就是上图右边这种情况，最小值在数组的第 1 位。

2. 比较中间和最右边可以确定最小值的位置

下图都满足中间 < 最右边，并且最小值都在前面。

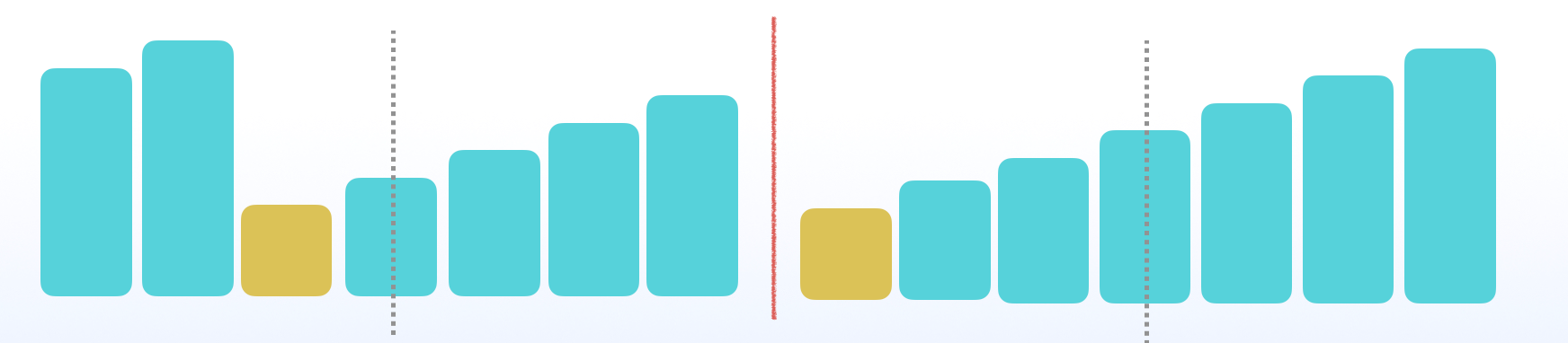
最极端的情况下，当中间 < 最右边时，最小值在中间。

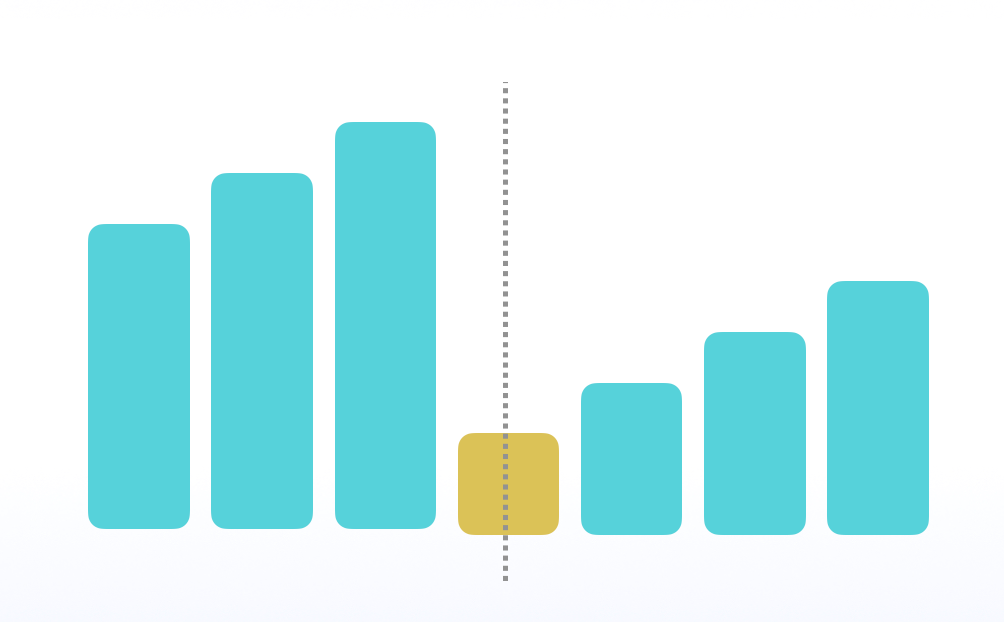
所以我们可以通过比较中间和最右边，知道旋转数组的最小值在哪里。如果要比较中间和最左边，需要做一些分类讨论，使得解决问题变得复杂。

左闭右闭

public class Solution {public int findMin(int[] nums) {int n = nums.length;int left = 0;int right = n - 1;while (left < right) {int mid = (left + right) / 2;if (nums[mid] < nums[right]) {// 下一轮搜索区间 [left..mid]right = mid;} else {// 因为题目中说：数组中不存在重复元素// 此时一定是 nums[mid] > nums[right]// 下一轮搜索区间 [mid + 1..right]left = mid + 1;}}// 一定存在最小元素，因此无需再做判断return nums[left];}
}

为什么这道题用 while (left < right)？

如果使用 <font style="color:rgb(15, 17, 21);background-color:rgb(235, 238, 242);">while (left <= right)</font> 配合 <font style="color:rgb(15, 17, 21);background-color:rgb(235, 238, 242);">right = mid</font>：

• 当 <font style="color:rgb(15, 17, 21);background-color:rgb(235, 238, 242);">left == right</font> 时，<font style="color:rgb(15, 17, 21);background-color:rgb(235, 238, 242);">mid = left = right</font>
• 如果进入 <font style="color:rgb(15, 17, 21);background-color:rgb(235, 238, 242);">right = mid</font> 分支，状态不变 → 死循环

所以这道题采用 <font style="color:rgb(15, 17, 21);background-color:rgb(235, 238, 242);">while (left < right)</font> 是为了：

1. 避免死循环：在区间长度为1时自动退出
2. 利用答案的唯一性：最终剩下的那个元素就是最小值

那为什么不能也把right = mid - 1呢？

问题所在：当 right = mid - 1跳过最小值！

154.寻找排序数组中的最小值②

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
• 若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须尽可能减少整个过程的操作步骤。

示例 1：

输入：nums = [1,3,5]
输出：1

示例 2：

输入：nums = [2,2,2,0,1]
输出：0

思路

比上一题多出的一个条件是：数组中可能存在重复元素

当 nums[mid] = nums[right] 时，只能把 right 排除掉

因为

• 如果去掉的数是最小值，那么 nums[mid] 也是最小值，这说明最小值仍然在数组中。
• 如果去掉的数不是最小值，那么我们排除了一个错误答案。

public class Solution {public int findMin(int[] nums) {int n = nums.length;int left = 0;int right = n - 1;while (left < right) {int mid = (left + right) / 2;if (nums[mid] == nums[right]) {right--;} else if (nums[mid] < nums[right]) {// 下一轮搜索区间 [left..mid]right = mid;} else {// 因为题目中说：数组中不存在重复元素// 此时一定是 nums[mid] > nums[right]// 下一轮搜索区间 [mid + 1..right]left = mid + 1;}}// 一定存在最小元素，因此无需再做判断return nums[left];}
}

33.搜索旋转排序数组

题目

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 向左旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 下标 3 上向左旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

思路

最简单的做法, 先找到最值将旋转数组分成两段有序数组，接下来在有序数组中找目标值就轻车熟路了。

• 先找到 「153. 寻找旋转排序数组中的最小值」的索引，由此可以将数组分为升序的两段。
• 根据 nums[0] 与 target 的关系判断 target 在左段还是右段，再对升序数组进行二分查找即可。
• 根据nums[n] 与 target的关系判断target在左段还是右段，再对升序数组进行二分查找即可

同样的思路可以解决「1095. 山脉数组中查找目标值」，即先找到山脉数组的峰顶「852. 山脉数组的峰顶索引」, 通过峰顶将山脉数组分为两段有序的数组，接下来就可以在有序数组中查找目标值了。

class Solution {public int search(int[] nums, int target) {int minValueIndex = findMin(nums);int n = nums.length - 1;if (target > nums[n]) {// target 在第一段(而且一定是旋转数组而非有序数组)return binarySearch(nums, 0, minValueIndex - 1, target);} else {// target 在第二段return binarySearch(nums, minValueIndex, n, target);}}// 153. 寻找旋转排序数组中的最小值（返回的是下标）public int findMin(int[] nums) {// 左闭右闭int left = 0;int right = nums.length - 1;while (left < right) {int mid = (left + right) / 2;if (nums[mid] < nums[right]) {right = mid;} else {left = mid + 1;}}return left;}public int binarySearch(int[] nums, int left, int right, int target) {while (left <= right) {int mid = (left + right) / 2;if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] < target) {left = mid + 1;} else {return mid;}}return -1;}
}

81.搜索旋转排序数组②

题目

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

思路

思维误区就是以为在上一题的基础上继续使用两次二分去做，但是忽略了问题

33题（无重复元素）的情况：

• 旋转点是唯一的
• 返回准确的最小值位置
• 数组被清晰地分为两个有序段
• ✅ 两次二分法有效

81题（有重复元素）的情况：

• 旋转点可能不唯一
• 返回的"最小值位置"可能不是真正的旋转点
• 划分的"有序段"实际上可能不是有序的

所以两次二分会退化为On，这题只能用一次二分！！！！

class Solution {public boolean search(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = (left + right) / 2;// 情况1：直接找到目标值if (nums[mid] == target) {return true;}// 情况2：无法判断哪边有序（重复元素导致）if (nums[mid] == nums[left] && nums[mid] == nums[right]) {left++;right--;}// 情况3：左段有序 (nums[mid] >= nums[left])else if (nums[mid] >= nums[left]) {if (target >= nums[left] && target < nums[mid]) {right = mid - 1;} else {left = mid + 1;}} else {    // 情况4：右段有序if (target <= nums[right] && target > nums[mid]) {left = mid + 1;} else {right = mid - 1;}}}return false;}
}

34. 在排序数组中查找元素的第一个位置和最后一个位置

题目

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

思路

定义函数，二分法找到>=这个元素的第一个位置，用左闭右闭

最后一个位置的话，我可以查找大于target+1的第一个位置，然后-1就得到了target的最后一个位置

class Solution {public int[] searchRange(int[] nums, int target) {int start = binarySearch(nums, target);if (start == nums.length || nums[start] != target) {return new int[]{-1, -1};}int end = binarySearch(nums, target + 1) - 1;return new int[]{start, end};}public int binarySearch(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = (left + right) / 2;if (nums[mid] < target) {left = mid + 1; // nums[left-1] < target} else {right = mid - 1; // nums[right+1] >= target}}// 循环结束后 left = right+1,所以 left 就是第一个 >= target 的元素下标return left;}
}

如果我的内容对你有帮助，请辛苦动动您的手指为我点赞，评论，收藏。感谢大家!!