daily notes[56]

the distribution function of the random vector

the application of Monte Carlo integration ,which is much better than using trapezoid integration, with JAX for multidimensional integration approximately calculate integartion through random sampling.

$${\int }_a^{b}f(x)dx\approx \frac{b-a}{N}\sum _{i=1}^{N}f(x_i),x_i\sim \mathcal{U}(a,b)$$

import jax
import jax.numpy as jnp
from jax import randomdef monte_carlo_integrate(f, a, b, key, n_samples=10000):"""计算一维积分 ∫[a, b] f(x) dx"""x_samples = random.uniform(key, (n_samples,), minval=a, maxval=b)f_values = f(x_samples)return (b - a) * jnp.mean(f_values)# 示例：积分 sin(x) 在 [0, π]
key = random.PRNGKey(42)
f = lambda x: jnp.sin(x)
result = monte_carlo_integrate(f, 0, jnp.pi, key)
print("∫sin(x)dx ≈", result)  # 理论值: 2.0

---

multidimensional integration ：
$${\int }_{a_1}^{b_1}{\int }_{a_2}^{b_2}{\int }_{a_3}^{b_3}f(x_1,x_2,x_3)d{x}_{1}d{x}_{2}d{x}_3\approx \frac{V}{N}\sum _{i=1}^{N}f({\mathbf{x}}_i)$$
$V={\prod }_{i=1}^3(b_i-a_i)$是积分区域体积

def monte_carlo_3d(f, a, b, key, n_samples=10000):"""计算三维积分 ∫[a1, b1]∫[a2, b2]∫[a3, b3] f(x1, x2, x3) dx1 dx2 dx3a, b: 各维度的积分限，如 a=[a1, a2, a3], b=[b1, b2, b3]"""x_samples = random.uniform(key, (n_samples, 3), minval=a, maxval=b)f_values = jax.vmap(f)(x_samples)  # 向量化计算volume = jnp.prod(jnp.array(b) - jnp.array(a))return volume * jnp.mean(f_values)# 示例：积分 x1 + x2 + x3 在 [0,1]×[0,1]×[0,1]
key = random.PRNGKey(42)
f = lambda x: x[0] + x[1] + x[2]
result = monte_carlo_3d(f, [0, 0, 0], [1, 1, 1], key)
print("∫∫∫(x1+x2+x3)dx1dx2dx3 ≈", result)  # 理论值: 1.5

from jax.scipy.stats import multivariate_normal# 定义三维高斯分布
mean = jnp.array([0.0, 1.0, -1.0])
cov = jnp.array([[1.0, 0.3, 0.1],[0.3, 1.0, 0.2],[0.1, 0.2, 1.0]
])# 联合PDF
joint_pdf = lambda x: multivariate_normal.pdf(x, mean=mean, cov=cov)# 蒙特卡洛计算CDF
def joint_cdf(a, b, c, key, n_samples=10000):# 在 [-5, a] x [-5, b] x [-5, c] 内均匀采样（近似无限积分）x_samples = random.uniform(key, (n_samples, 3), minval=jnp.array([-5.0, -5.0, -5.0]),maxval=jnp.array([a, b, c]))pdf_values = jax.vmap(joint_pdf)(x_samples)volume = (a - (-5)) * (b - (-5)) * (c - (-5))return volume * jnp.mean(pdf_values)key = random.PRNGKey(42)
print("P(X1≤0.5, X2≤1.5, X3≤-0.5) ≈", joint_cdf(0.5, 1.5, -0.5, key))

方法	优点	缺点
蒙特卡洛 (JAX)	易并行化，支持高维，GPU加速	结果有随机性
梯形积分	确定性结果	高维计算慢，内存占用大
SciPy quad/dblquad	高精度	不支持自动微分/GPU

---

the density funtion of the random vector

the density function is the partial derivative of X as follows:

to get the united density and the edge endsity from Python code with JAX

• the united density
  we can explain the united density with an example which is three-dimensional Gaussian distrubution.

import jax
import jax.numpy as jnp
from jax.scipy.stats import multivariate_normal# 定义均值向量和协方差矩阵
mean = jnp.array([0.0, 1.0, -1.0])  # 3维均值
cov = jnp.array([[1.0, 0.3, 0.1],[0.3, 1.0, 0.2],[0.1, 0.2, 1.0]
])  # 3x3 对称正定协方差矩阵# 联合概率密度函数
def joint_pdf(x):return multivariate_normal.pdf(x, mean=mean, cov=cov)# 测试点
x_test = jnp.array([0.5, 1.5, -0.5])
print("联合概率密度:", joint_pdf(x_test))

PS E:\learn\learnpy> & D:/Python312/python.exe e:/learn/learnpy/learn1.py
联合概率密度: 0.051931586

# 检查对称性
is_symmetric = jnp.allclose(cov, cov.T)
print("协方差矩阵是否对称:", is_symmetric)# 检查正定性（通过Cholesky分解）
try:jnp.linalg.cholesky(cov)print("协方差矩阵正定")
except:print("协方差矩阵非正定！需修正")

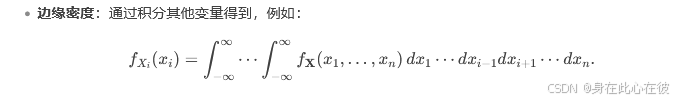
it is the best way of calculating the integral with JAX to use trapezoid method because that JAX has inability to provide common API function such as SciPy's quad.

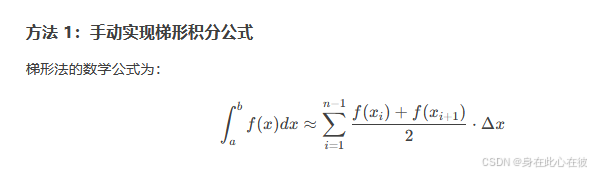
import jax.numpy as jnpdef trapz(y, x):"""手动实现梯形积分，兼容 JAX"""return jnp.sum((y[:-1] + y[1:]) / 2 * jnp.diff(x))# 示例：积分 sin(x) 在 [0, π]
x = jnp.linspace(0, jnp.pi, 1000)
y = jnp.sin(x)
result = trapz(y, x)
print(result)  # 应接近 2.0

you can also use jax.scipy.integrate.trapezoid.

import jax.numpy as jnpfrom jax.scipy.integrate import trapezoidx = jnp.linspace(0, jnp.pi, 1000)
y = jnp.sin(x)
result = trapezoid(y, x)
print(result)  # 输出 2.0

a complete example for computing the edge endsity be shown as follows:

from jax.scipy.integrate import trapezoid
import jax
import jax.numpy as jnpimport jax
from jax.scipy.stats import multivariate_normal# 定义三维高斯参数
mean = jnp.array([0.0, 1.0, -1.0])
cov = jnp.array([[1.0, 0.3, 0.1],[0.3, 1.0, 0.2],[0.1, 0.2, 1.0]
])# 联合概率密度函数
def joint_pdf(x):return multivariate_normal.pdf(x, mean=mean, cov=cov)# 计算边缘密度 p(x1) = ∫∫ p(x1, x2, x3) dx2 dx3
def marginal_pdf1(x1, n_samples=100):x2 = jnp.linspace(-5, 5, n_samples)  # 积分范围近似x3 = jnp.linspace(-5, 5, n_samples)X2, X3 = jnp.meshgrid(x2, x3)# 向量化计算积分integrand = lambda x2, x3: joint_pdf(jnp.array([x1, x2, x3]))y = jax.vmap(jax.vmap(integrand))(X2, X3)# 双重梯形积分dx2 = x2[1] - x2[0]dx3 = x3[1] - x3[0]return trapezoid(trapezoid(y, dx=dx2), dx=dx3)# 计算边缘密度 p(x2) = ∫∫ p(x1, x2, x3) dx1 dx3
def marginal_pdf2(x2, n_samples=100):x1 = jnp.linspace(-5, 5, n_samples)  # 积分范围近似x3 = jnp.linspace(-5, 5, n_samples)X1, X3 = jnp.meshgrid(x1, x3)# 向量化计算积分integrand = lambda x1, x3: joint_pdf(jnp.array([x1, x2, x3]))y = jax.vmap(jax.vmap(integrand))(X1, X3)# 双重梯形积分dx1 = x1[1] - x1[0]dx3 = x3[1] - x3[0]return trapezoid(trapezoid(y, dx=dx1), dx=dx3)# 测试
print("边缘密度 p(x2=0.6):", marginal_pdf2(0.6))
print("边缘密度 p(x1=0.3):", marginal_pdf1(0.3))

边缘密度 p(x2=0.6): 0.36825997
边缘密度 p(x1=0.3): 0.38137165

conditional probability density function

now,we try to solve the problem that how to calculate the conditional probability density of three dimensions random vectors which conform to joint gauss distribution .

the joint gauss distribution was defined as following Python codes:

import jax
import jax.numpy as jnp
from jax.scipy.stats import multivariate_normal# 定义均值和协方差矩阵 (3维)
mu = jnp.array([1.0, -1.0, 0.5])  # [μ_X, μ_Y, μ_W]# 协方差矩阵 (3x3)
Sigma = jnp.array([[2.0, 0.5, -0.3],   # X的方差和协方差[0.5, 1.0, 0.2],     # Y的方差和协方差[-0.3, 0.2, 1.5]     # W的方差和协方差
])# 检查协方差矩阵是否正定
assert jnp.all(jnp.linalg.eigvals(Sigma) > 0), "协方差矩阵必须正定！"

the conditional probability distribution of X when Y=y and W=w is as follows:

# 分块矩阵索引
# Z = [X, Y, W], 条件分布 P(X | Y=y, W=w)
# 分割协方差矩阵
Sigma_XX = Sigma[0, 0].reshape(1, 1)          # Var(X)
Sigma_XY = Sigma[0, 1:].reshape(1, 2)          # Cov(X, [Y, W])
Sigma_YY = Sigma[1:, 1:]                       # Var([Y, W])
Sigma_YX = Sigma_XY.T# 给定观测值
y_observed = jnp.array([-0.5, 1.0])  # [y, w]# 计算条件均值和协方差
Sigma_YY_inv = jnp.linalg.inv(Sigma_YY)
mu_X_given_YW = mu[0] + Sigma_XY @ Sigma_YY_inv @ (y_observed - mu[1:])
Sigma_X_given_YW = Sigma_XX - Sigma_XY @ Sigma_YY_inv @ Sigma_YXprint("Conditional mean (X | Y, W):", mu_X_given_YW)
print("Conditional variance (X | Y, W):", Sigma_X_given_YW)

jax.numpy

jax.numpy.linspace

jax.numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0, *, device=None)

return a set of numbers separated with the fixed interval evenly.

import jax
import jax.numpy as jnp
print(jnp.linspace(11,55,5))

[11. 22. 33. 44. 55.]

import jax
import jax.numpy as jnp
print(jnp.linspace(11,55,5,retstep=True))

(Array([11., 22., 33., 44., 55.], dtype=float32), Array(11., dtype=float32))

the function can also use for generating multiple dimensions array.

import jax
import jax.numpy as jnp
print(jnp.linspace(jnp.array([1,11]),jnp.array([5,55]),5))

[[ 1. 11.][ 2. 22.][ 3. 33.][ 4. 44.][ 5. 55.]]

jax.numpy.arange

the function make also a sequence consisted of number and they are separated by equal interval.the function is similar as jax.numpy.linspace.but the important difference is that jax.numpy.arange runing depend on the step which means interval and the jax.numpy.linspace is applied with the argument num which represents the number of numbers.

jax.numpy.arange(start, stop=None, step=None, dtype=None, *, device=None)

[11 22 33 44]

there are a difference which is easily ignored usually that the stop at jax.numpy.arange means the end but excusive itself.by the way, jax.numpy.arange’s arguments must be scalars.
the following code will get a error when it runing.

print(jnp.arange(jnp.array([1,11]),jnp.array([5,55]),11))

jax.typing

1. the function annotations applied for static type checking maybe become a integral python coding standard.
2. jax.Array is the base class represented array.
3. to annotate in python project.

• Level 1: Annotations as documentation

def f(x: jax.Array) -> jax.Array:  # type annotations are valid for traced and non-traced types.return x

• Level 2: Annotations for intelligent autocomplete
  the many modern IDEs such as vscode make use of the type annotations in intelligent code completion systems.
• Level 3: Annotations for static type-checking

4. the package development with JAX must abide by two python type checking facilities including pytype developed by google , and mypy which known as the most popular static type checking tools.And beyond that, JAX will face chanllenges such as array duck-typing,transformations and decorators,array annotation lack of granularity and imprecise APIs inherited from NumPy.
5. JAX provided that static type annotations and runtime instance checks for duck-typed objects.

• Static type annotations

from typing import Union
from jax import Array, jit
from jax.core import Tracer
import jax.numpy as jnpArrayAnnotation = Union[Array, Tracer]@jit
def f(x: ArrayAnnotation) -> ArrayAnnotation:assert isinstance(x, (Array, Tracer))  # Explicit checkreturn x * 2x = jnp.array([1.0, 2.0, 3.0])
result = f(x)
print(result)  # [2. 4. 6.] (jax.Array)@jit
def g(x):return f(x)  # `x` is a Tracer here!print(g(x))      # Same output, but internally tracedfrom jax import graddf_dx = grad(lambda x: f(x).sum())  # Works with tracers
print(df_dx(x))  # [2. 2. 2.] (gradient of x*2)f("invalid_input")
f(234)

[2. 4. 6.]
[2. 4. 6.]
[2. 2. 2.]
Traceback (most recent call last):File "e:\learn\learnpy\l2.py", line 29, in <module>f("invalid_input")
TypeError: Error interpreting argument to <function f at 0x0000018EEFD999E0> as an abstract array. The problematic value is of type <class 'str'> and was passed to the function at path x.
This typically means that a jit-wrapped function was called with a non-array argument, and this argument was not marked as static using the static_argnums or static_argnames parameters of jax.jit.
--------------------
For simplicity, JAX has removed its internal frames from the traceback of the following exception. Set JAX_TRACEBACK_FILTERING=off to include these.

• Runtime instance checks

from typing import Union
from jax import Array, jit
from jax.core import Tracer
import jax.numpy as jnpArrayInstance = Union[Array, Tracer]@jit
def f(x):return isinstance(x, ArrayInstance)x = jnp.array([1, 2, 3])
assert f(x)       # x will be an array
assert jit(f)(x)  # x will be a tracer

Diagonal Matrix

1. one dimension array which its elements be placed in the diagonal matrix can be convert to the diagonal matrix through jnp.diag.

import jax.numpy as jnp# 从一维数组创建对角矩阵
vec = jnp.array([1, 2, 3])
diag_matrix = jnp.diag(vec)  # 对角线为 [1, 2, 3]，其余为 0
print(diag_matrix)

of course,you can change reversely such as grabing the elements from a diagonal matrix.

matrix = jnp.array([[1, 0, 0], [0, 2, 0], [0, 0, 3]])
extracted_vec = jnp.diag(matrix)  # 返回 [1, 2, 3]

defining a unit matrix can apply jnp.eye.

import jax.numpy as jnp# 从一维数组创建对角矩阵
vec_I = jnp.eye(3)
print(vec_I)

now ,we write a bit of python code for illustrating $AI=IA=A$.

import jax
import jax.numpy as jnpkey = jax.random.PRNGKey(42)  # 随机种子
A = jax.random.uniform(key, shape=(5, 3), minval=0.0, maxval=10.0)
print(A)
vec_I = jnp.eye(3)
print(vec_I)
print(A @ vec_I)
jnp.dot(A, vec_I)

[[4.8870955 6.7979717 6.162715 ][5.610161  4.506446  5.858659 ][0.7480943 7.7513337 6.9895926][8.1863365 3.503052  8.7282   ][9.258814  8.601307  4.775541 ]]
[[1. 0. 0.][0. 1. 0.][0. 0. 1.]]
[[4.8870955 6.7979717 6.162715 ][5.610161  4.506446  5.858659 ][0.7480943 7.7513337 6.9895926][8.1863365 3.503052  8.7282   ][9.258814  8.601307  4.775541 ]]

to create a random matrix is as follows:

key = jax.random.PRNGKey(0)
random_matrix = jax.random.normal(key, (3, 3))

you can generate a matrix from list ,for example

matrix = jnp.array([[1, 2], [3, 4]])

references

1. https://docs.jax.dev/
2. deepseek