关于红黑树删除节点操作的完整推导

最近算法学了红黑树，但是老师没讲删除操作。

看了很多网上的博客，都是根据具体的节点例子去推导的，难免在枚举过程中有些情况会遗漏，并且红黑树删除还有迭代的更新过程。

所以还是打算按照子树形式，完整地推了一下红黑树删除操作。

有些分类可能可以简化，有些地方可能会有笔误，还请各路大神批评指正。

一、复习以及一个推论

二叉查找树删除节点：

没有儿子：直接删除

一个儿子：删除后用该儿子顶上

两个儿子：通常找前驱或者后继来替换，转换为一个儿子的情况

红黑树性质：（二叉查找树性质省略了）

（1）根节点与叶节点（NIL）均为黑色

（2）红色节点下方必须均为黑色节点（两个红色节点不相邻）

（3）从任意节点出发向下走，到达任意一个叶子所经过的黑节点个数相等

黑高BH(x)：从节点x出发，到达叶子所经过的黑色节点个数（不包含出发点x）

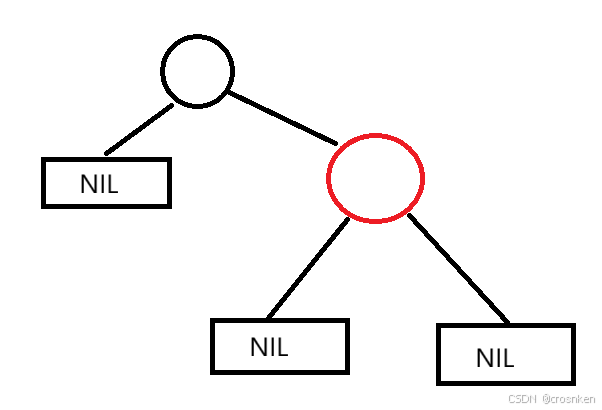
推论：在红黑树中，只有一个儿子的节点的BH必定为1，且必定为黑色

很好证明，因为从它出发，到达没有儿子的一边时，只会经过一个NIL节点，所以BH一定为1

由于它又有一个儿子，这个儿子又不能贡献黑色节点的数量，那么这个儿子必定为红色节点

由于两个红色节点不能相邻，所以它必须是黑色节点。

更具体一点，这个儿子还必须是一个红色末端节点，它的下面都是NIL节点

二、删除操作

1、对于两个儿子的节点，查找其前驱或后继进行替换（只替换值，不改变颜色），变为删除一个儿子的节点或者没有儿子的节点。

2、对于一个儿子的节点，由于上述推论，它一定是黑色节点，删除它就是用它唯一的儿子去替换它。这一类和删除没有儿子的黑色节点这一类是一样的，它们所在的子树贡献的黑高BH都会因为删除它而减少1。

3、对于没有儿子的红色节点，直接删除即可。

接下来我们详细讨论2。（即删除黑点的情况）

首先删除一个黑点，必定会导致某个子树贡献的黑高减1，从广义来看，我们只需要对于左右儿子节点BH值不同的子树进行维护即可。

由于二叉树是对称的，所以我们只讨论左子树发生改变的情况

默认发生改变的节点为u，其父亲节点为f，兄弟节点为v

u所在的子树记为A，v的两个儿子分别所在的子树根节点记为B和C

初始条件BH(f->u)=x（从f出发，经过点u到达叶子节点所经过的黑点个数，表示u的子树向上能够贡献x个黑点）

删除后情况，BH(f->u)=x-1

1、当f为红色

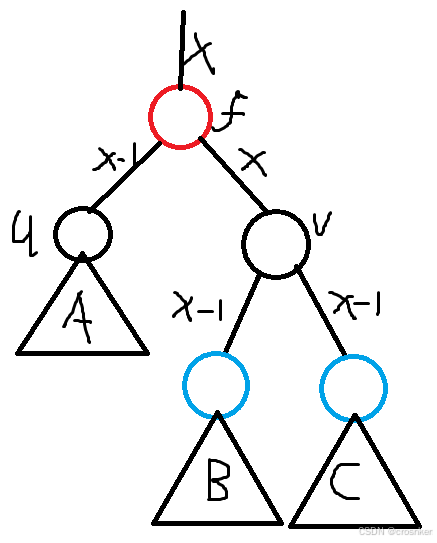
（这是u的黑高发生改变后还未维护的图，蓝色表示未知颜色的点）

图中边上标注的数字x，表示该边下方的子树贡献的路径黑点个数为x

此时，u子树无法向上贡献x个黑点，所以需要调整

我们对v进行一个左旋之后可以得到下图：

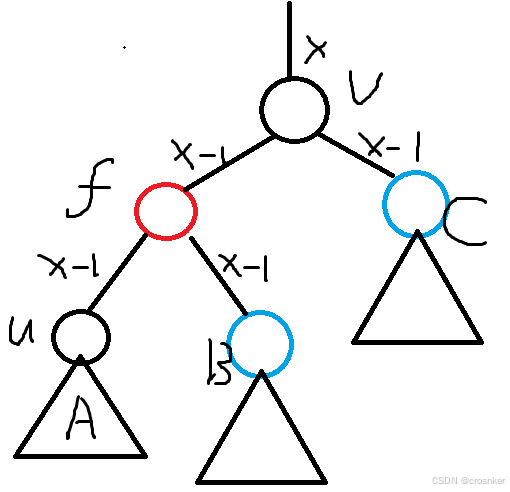
由于子树之间是独立的，所以每个子树贡献出来的BH都是不变的

现在的关键问题就是节点f和节点B是不是同时为红色

如果B不是红色，则万事大吉，不需要再变了。

如果B是红色，此时，我们发现这个情况和插入红色节点的情况是一样的，需要判断B的叔节点C的颜色来调整，这里就略过了。

另外的解法：

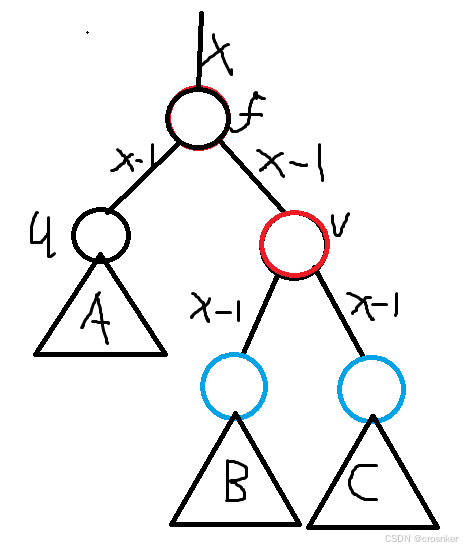
有些文章中会写，把节点f和节点v的颜色交换即可。

B和C的颜色目前都是不确定的，如果BC都是黑色，那就没事，如果BC都是红色，那就两个都变成黑色，如果BC一红一黑，那就按照插入红点的更新方法来解决即可。（记为✳下传解法）

这个解法确实更加优秀，省去了初始的旋转。

2、当f为黑色

（1）u为红色

虽然在删除中的迭代只可能是由黑色顶点向上的迭代，但是为了逻辑完整还是加入了红色节点BH变为x-1的情况。

此时只需要把u变为黑色即可。

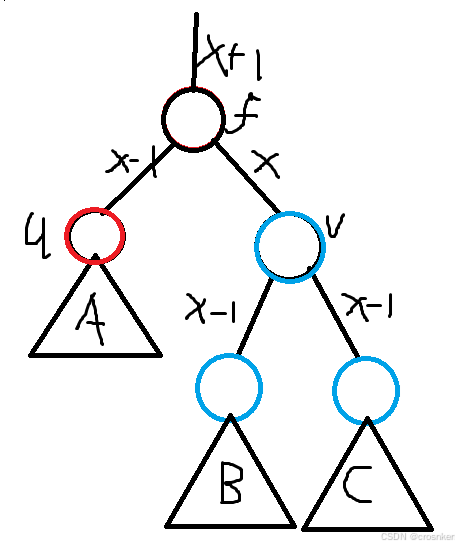
（2）u为黑色，v为红色

我们发现，这个时候u提供的路径黑点数和f需要提供的路径黑点数已经相差2了

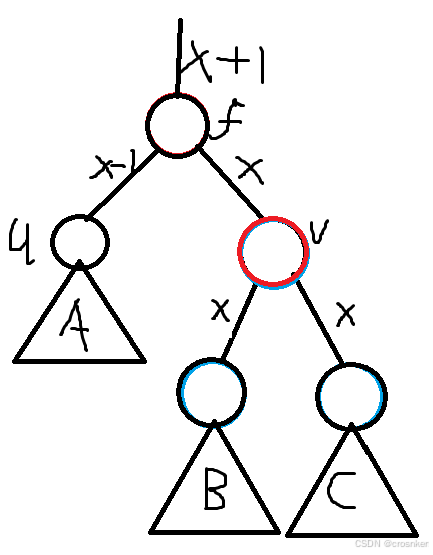
我们左旋节点v，把f作为黑点分给u，然后再把v变成黑色，通过u提供贡献上去的路径就满足条件了。

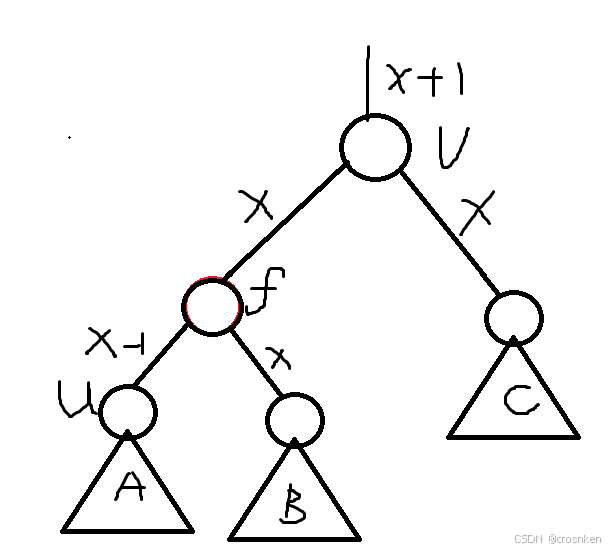
但是B向上的路径还不满足条件，我们把B变为红点就可以满足条件。

将B变为红点之后还需要进行✳下传解法，根据B子树中的情况更新

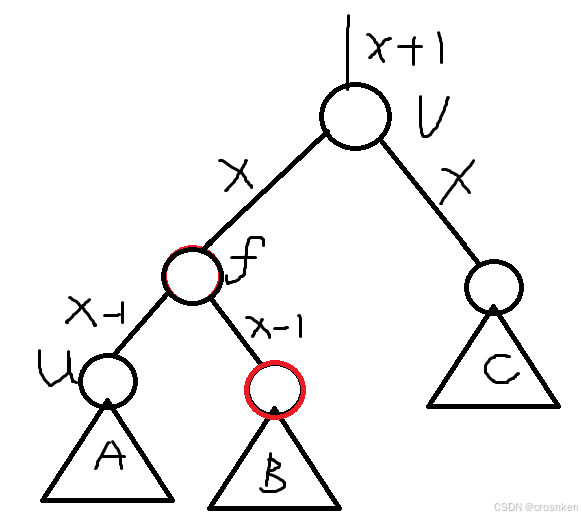
（3）u为黑色，v为黑色

这是最麻烦的一个情况，也是导致了删除可能发生迭代的情况

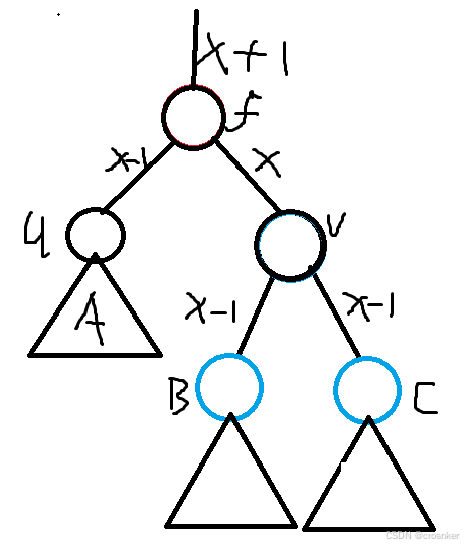
现在麻烦之处在于，ABC三个子树都只能贡献x-1的黑高，想要保持f子树贡献x+1的黑高不变，需要根据B和C的颜色来具体分析。

a.节点C是红色

我们可以直接左旋v，把u和B分到f的下面，然后让C从红色变成黑色，两边都可以凑出x，最终的贡献就是x+1，保持不变。

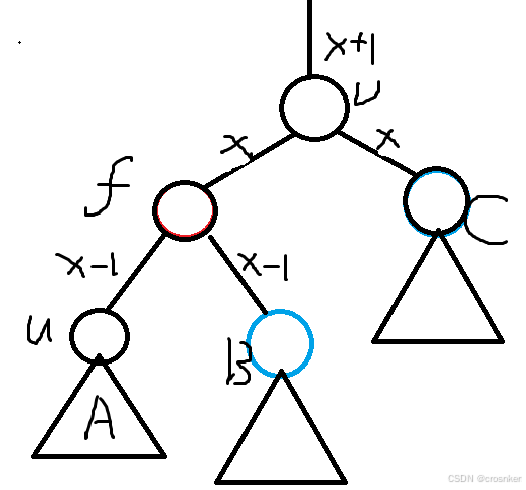
b.节点B是红色

那么B的下面必定存在两个黑色点α和β，并且它们对黑点的贡献和B点的贡献相同，都是x-1。

这时我们发现，只要把这4个贡献为x-1的子树（A，α，β，C）拼起来，就一定可以让这一整个结构黑点贡献为x+1。

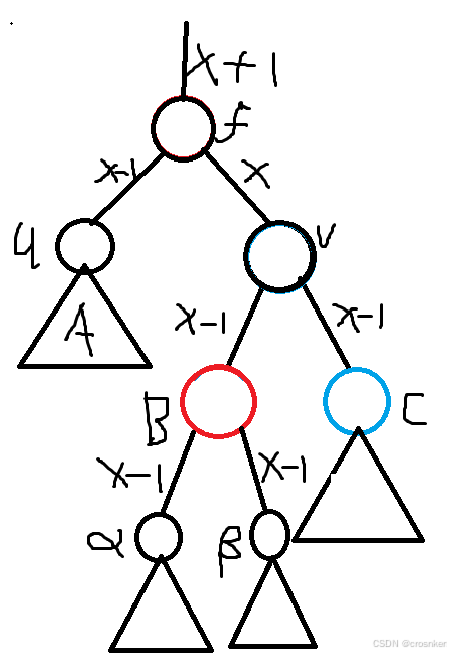
我们将B进行一次右旋和一次左旋，转到最上面并染成黑色。

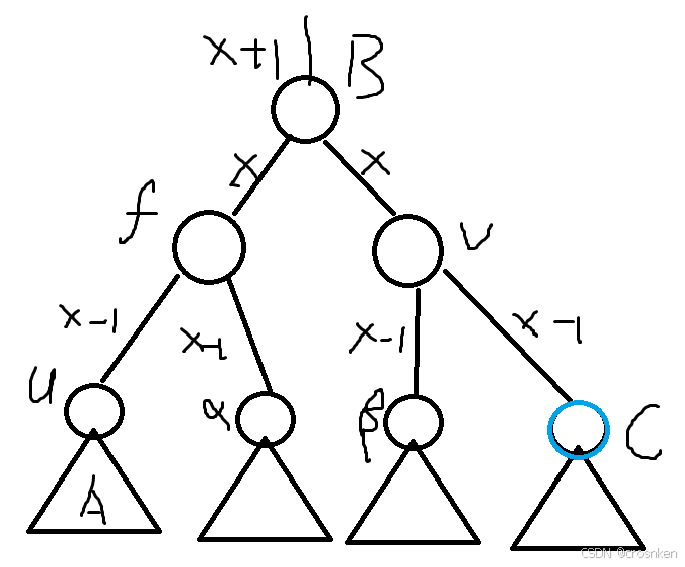
这样就保持了整个子树合法与对外贡献不变。

c.BC都是黑色

这是最难受的情况，意味着我们不能通过把红点变成黑点来平衡两边的黑高了。

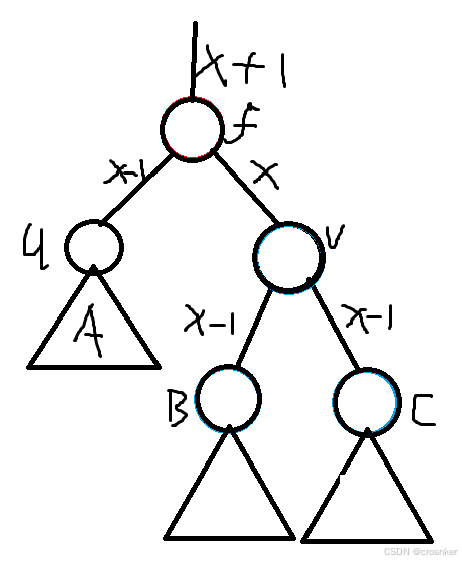
其实解法也很简单，退一步海阔天空，把v染成红色，这样v向上的贡献就变成了x-1，f节点也就平衡了。

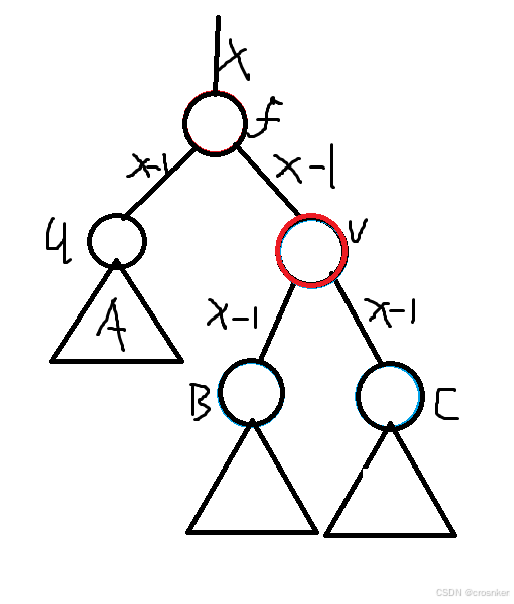
唯一的问题在哪里呢，就是f节点向上的贡献从x+1变成了x。

所以还需要迭代向上更新，把f视作u，把f的父亲视作f，再进行以上操作。

三、关于时间复杂度和旋转次数

对上面的所有情况分一下类

结束更新：2(1)，2(3)a，2(3)b

需要修复可能的红色冲突：1，2(2)

需要向上迭代：2(3)c

对于红色冲突修复，本质和插入的时间复杂度是一样的

向上迭代也最多迭代树高次，所以整体时间复杂度是O(logn)的

对于旋转次数

红色冲突修复时，最多造成两次旋转，2(2)还需要一次旋转，所以最多进行三次旋转。

向上迭代的情况只会改变点的颜色，不贡献旋转次数。

结束更新的情况，最多也只造成两次旋转。

综上，一次删除操作最多进行三次旋转。