双三次插值（BiCubic Interpolation）超分算法详解

双三次插值（BiCubic Interpolation）超分算法详解

一、算法背景

在数字图像处理领域，图像缩放（Scaling）是一项基础且频繁使用的操作，其核心需求是将图像从原始分辨率转换到目标分辨率。超分辨率重建（Super-Resolution）作为图像缩放的重要分支，专注于将低分辨率图像（LR）提升至更高分辨率（HR），以满足高清显示、细节分析等应用场景。

随着显示技术的发展（如 4K/8K 屏幕普及）和图像采集设备的限制（如低像素摄像头），超分技术的需求日益迫切。传统超分方法主要基于插值理论，通过数学计算推测新像素值，而双三次插值正是其中性能优异的经典算法。

与其他插值方法相比，双三次插值在以下场景中表现突出：

• 图像放大倍数适中（2-4 倍）时的质量需求
• 对边缘平滑度要求较高的场景（如印刷、数字绘画）
• 计算资源有限，无法运行深度学习模型的环境

二、算法由来

双三次插值的发展源于对更优图像缩放质量的追求，其思想可追溯至信号处理中的插值理论。

早期的图像缩放主要采用最邻近插值（Nearest Neighbor）和双线性插值（Bilinear Interpolation）：

• 最邻近插值直接取距离最近的像素值，计算简单但会产生严重锯齿
• 双线性插值考虑周围 4 个像素的加权平均，边缘平滑度提升但仍显模糊

为解决这些问题，研究者们提出了基于更高阶多项式的插值方法。三次插值（Cubic Interpolation）首先在一维信号处理中得到应用，通过三次多项式拟合相邻数据点，实现更平滑的过渡。

双三次插值则是将一维三次插值扩展到二维图像领域的成果，其核心思想由 G. Gordon 在 1984 年的论文中正式提出。该算法通过考虑目标像素周围 4×4 共 16 个像素的信息，使用三次卷积核计算权重，在平滑度和细节保留之间取得了良好平衡，成为此后数十年图像编辑软件（如 Photoshop）和图形库（如 OpenCV）的默认缩放算法。

三、算法原理与实现流程

1. 核心数学基础

（1）三次卷积核函数

双三次插值的核心是三次卷积核，用于计算不同距离像素的权重，公式如下（参数 a 通常取 - 0.5）：

$$W(t)=\{\begin{array}{ll}(a+2)|t{|}^3-(a+3)|t{|}^2+1& \text{, 当 }|t|\le 1\\ a|t{|}^3-5a|t{|}^2+8a|t|-4a& \text{, 当 }1<|t|<2\\ 0& \text{, 当 }|t|\ge 2\end{array}$$
该函数特性：距离越近的像素权重越大，超过 2 个像素距离则无影响。

（2）坐标映射关系

设缩放因子为 s，超分后图像的像素 (i,j) 对应原始图像的坐标为：

$$x=j/s,y=i/s$$

2. 完整实现流程

步骤 1：坐标映射（定位原始图像中的参考点）

对于超分后图像的每个像素 (i,j)（新坐标），需先找到它在原始图像中的「对应位置」（通常是小数坐标）。

• 计算方式：

  设缩放因子为 s，则新坐标 (i,j) 对应原始图像的坐标为：

  x = j / s，y = i / s

  （例如：2 倍放大时，新图像的 (2,4) 对应原始图像的 (1,2)）

• 实际情况：

  多数时候 x 和 y 是小数（如缩放 1.5 倍时，新坐标 (3,3) 对应原始坐标 (2,2)），因此需要找周围的整数坐标像素作为参考。

步骤 2：选择邻域像素（16 个参考点）

双三次插值会选取原始图像中围绕 (x,y) 的 4×4 共 16 个像素 作为参考（这是它比双线性插值（4 个像素）效果更好的关键）。

具体操作：

1. 取 x 的整数部分 x0 = floor(x)，小数部分 dx = x - x0

   （例如 x=2.3，则 x0=2，dx=0.3）

2. 取 y 的整数部分 y0 = floor(y)，小数部分 dy = y - y0

3. 16 个参考点的坐标为：

   (x0-1 + l, y0-1 + k)，其中 l=0,1,2,3，k=0,1,2,3

边界处理：

若参考点超出原始图像范围（如 x-1 < 0），则取边界像素（如 x=0）。

步骤 3：计算权重（基于三次卷积核）

16 个参考点对新像素的影响程度（权重）由「三次卷积核函数」计算，该函数根据距离（dx 或 dy）生成权重，距离越近权重越大。

三次卷积核函数（核心公式）

设 t 为距离（dx 或 dy），常用参数 a=-0.5（效果较平滑），则：
$$W(t)=\{\begin{array}{ll}(a+2)|t{|}^3-(a+3)|t{|}^2+1& \text{, 当 }|t|\le 1\\ a|t{|}^3-5a|t{|}^2+8a|t|-4a& \text{, 当 }1<|t|<2\\ 0& \text{, 当 }|t|\ge 2\end{array}$$

函数图像特点：

是一个平滑的三次曲线，在 t=0 时权重最大（1.0），t=1 时权重 0，t=2 时权重 0，中间连续变化。

计算水平和垂直权重

• 水平方向权重（4 个）：

  基于 dx 计算，对应 x0-1, x0, x0+1, x0+2 四个位置，记为 w_x0, w_x1, w_x2, w_x3。

• 垂直方向权重（4 个）：

  基于 dy 计算，对应 y0-1, y0, y0+1, y0+2 四个位置，记为 w_y0, w_y1, w_y2, w_y3。

• 每个参考点的最终权重：

  水平权重 × 垂直权重（如 (x0, y0) 的权重为 w_x1 × w_y1）。

  水平方向权重（4 个）：基于 dx 计算，对应 x_0-1, x_0, x_0+1, x_0+2 四个位置：
  $$w_x(l)=W(1+dx-l)\text{其中 }l=0,1,2,3$$
  垂直方向权重（4 个）：基于 dy 计算，对应 y_0-1, y_0, y_0+1, y_0+2 四个位置：
  $$w_y(k)=W(1+dy-k)\text{其中 }k=0,1,2,3$$
  最终权重：每个参考像素 (x_0-1+l, y_0-1+k) 的总权重为水平权重与垂直权重的乘积：
  $$w(l,k)=w_x(l)\times w_y(k)$$

步骤 4：加权求和（计算新像素值）

将 16 个参考点的像素值与对应权重相乘后求和，得到新像素的最终值。

• 公式：

  新像素值 = Σ(参考点像素值 × 对应权重)

  

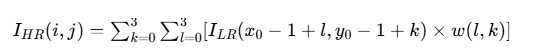
  $$I_{H}R(i,j)=su{m}_{k=0}^{3}su{m}_{l=0}^3[I_{L}R(x_0-1+l,y_0-1+k)\times w(l,k)]$$

• 范围修正：

  由于像素值范围是 0~255（8 位图像），需对结果进行裁剪（clip(0, 255)），避免超出范围。

• 彩色图像处理：

  对 RGB 三个通道分别执行上述计算，最后合并通道。
  $$R_{H}R(i,j)=su{m}_{k=0}^{3}su{m}_{l=0}^3[R_{L}R(x_0-1+l,y_0-1+k)\times w(l,k)]$$

  $$G_{H}R(i,j)=su{m}_{k=0}^{3}su{m}_{l=0}^3[G_{L}R(x_0-1+l,y_0-1+k)\times w(l,k)]$$

  $$B_{H}R(i,j)=su{m}_{k=0}^{3}su{m}_{l=0}^3[B_{L}R(x_0-1+l,y_0-1+k)\times w(l,k)]$$

  

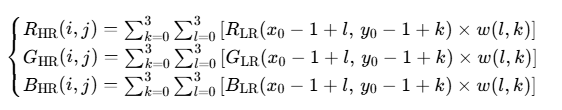
示例：简化计算过程

假设原始图像中某区域像素值如下（灰度图），需计算超分后某像素的值：

原始像素（4×4邻域）：
[ [10, 20, 30, 40],[50, 60, 70, 80],[90, 100, 110, 120],[130, 140, 150, 160] ]

1. 新像素对应原始坐标 (x=2.3, y=1.4) → x0=2, dx=0.3；y0=1, dy=0.4。
2. 计算水平权重（基于 dx=0.3）和垂直权重（基于 dy=0.4）。
3. 16 个像素分别乘以对应的 w_x×w_y 后求和，得到新像素值。

python实现

import numpy as np
from PIL import Image
import mathdef cubic_kernel(x, a=-0.5):"""三次卷积核函数"""x = abs(x)if x <= 1:return (a + 2) * math.pow(x, 3) - (a + 3) * math.pow(x, 2) + 1elif x < 2:return a * math.pow(x, 3) - 5 * a * math.pow(x, 2) + 8 * a * x - 4 * aelse:return 0def bicubic_interpolation(image, scale_factor):"""双三次插值超分函数参数:image: 输入图像（PIL Image对象）scale_factor: 缩放因子返回:超分后的图像（PIL Image对象）"""# 将图像转换为numpy数组img_array = np.array(image)if len(img_array.shape) == 3:height, width, channels = img_array.shapeis_gray = Falseelse:height, width = img_array.shapechannels = 1is_gray = True# 计算输出图像的尺寸new_height = int(height * scale_factor)new_width = int(width * scale_factor)# 创建输出数组if is_gray:output = np.zeros((new_height, new_width), dtype=np.uint8)else:output = np.zeros((new_height, new_width, channels), dtype=np.uint8)# 计算缩放比例的倒数inv_scale = 1.0 / scale_factor# 对输出图像的每个像素进行计算for i in range(new_height):# 计算在原始图像中的对应位置y = i * inv_scale# 确定参考点y0 = math.floor(y)dy = y - y0# 计算垂直方向的权重v_weights = [cubic_kernel(1 + dy),cubic_kernel(dy),cubic_kernel(1 - dy),cubic_kernel(2 - dy)]for j in range(new_width):# 计算在原始图像中的对应位置x = j * inv_scale# 确定参考点x0 = math.floor(x)dx = x - x0# 计算水平方向的权重h_weights = [cubic_kernel(1 + dx),cubic_kernel(dx),cubic_kernel(1 - dx),cubic_kernel(2 - dx)]# 计算16个参考点的加权平均pixel_value = 0.0for k in range(4):# 获取y方向的参考坐标，处理边界情况y_coord = y0 - 1 + kif y_coord < 0:y_coord = 0elif y_coord >= height:y_coord = height - 1for l in range(4):# 获取x方向的参考坐标，处理边界情况x_coord = x0 - 1 + lif x_coord < 0:x_coord = 0elif x_coord >= width:x_coord = width - 1# 获取像素值并应用权重weight = v_weights[k] * h_weights[l]if is_gray:pixel_value += img_array[y_coord, x_coord] * weightelse:for c in range(channels):output[i, j, c] += img_array[y_coord, x_coord, c] * weight# 确保像素值在有效范围内if is_gray:output[i, j] = np.clip(pixel_value, 0, 255).astype(np.uint8)else:for c in range(channels):output[i, j, c] = np.clip(output[i, j, c], 0, 255).astype(np.uint8)# 将numpy数组转换回PIL图像并返回return Image.fromarray(output)def super_resolve_image(input_path, output_path, scale_factor):"""使用双三次插值进行图像超分并保存结果参数:input_path: 输入图像路径output_path: 输出图像路径scale_factor: 缩放因子"""# 打开图像img = Image.open(input_path)# 进行双三次插值超分super_res_img = bicubic_interpolation(img, scale_factor)# 保存结果super_res_img.save(output_path)print(f"超分完成，结果已保存至 {output_path}")# 示例用法
if __name__ == "__main__":# 输入图像路径input_image = "input.jpg"# 输出图像路径output_image = "output_bicubic.jpg"# 缩放因子（例如2表示将图像放大2倍）scale = 2# 执行超分super_resolve_image(input_image, output_image, scale)