构建AI智能体：四十四、线性回归遇见大模型：从数学原理到智能实战

一、什么是线性回归

        结合我们生活中例子，如果你是一个水果店老板，你想知道“草莓的重量”和“它的价格”之间有什么关系。凭经验你知道，越重的草莓肯定越贵。线性回归就是帮你把这种模糊的经验，变成一个精确的数学公式。

核心思想：找到一个线性方程（一条直线），来最好地描述自变量 (X)（比如：重量）和因变量 (Y)（比如：价格）之间的关系。

公式：Y = wX + b

• Y: 我们要预测的值（价格）
• X: 我们已知的、用来预测的特征（重量）
• w: 权重，代表直线的斜率。意思是“X每增加1个单位，Y会增加w个单位”。比如w=5，就是重量每增加1克，价格增加5元。
• b: 偏置，代表直线的截距。意思是“即使草莓重量为0，它也有一个基础价值”（比如包装盒的成本），但现实中这个值可能为0或很小。

可视化的理解：我们用Python生成一组模拟数据，直观感受线性关系：

import numpy as np
import matplotlib.pyplot as plt# 生成带噪声的线性数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # 特征：100个样本，范围[0,2)
y = 4 + 3 * X + np.random.randn(100, 1)  # 真实关系：y=4+3x+噪声# 绘制散点图
plt.scatter(X, y, alpha=0.6)
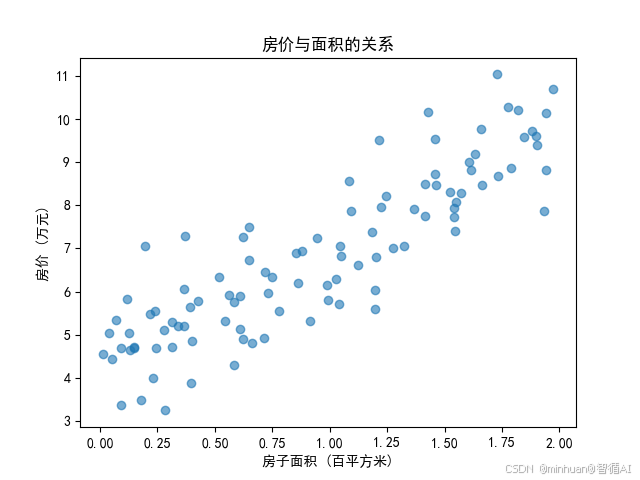
plt.xlabel("房子面积 (百平方米)")
plt.ylabel("房价 (万元)")
plt.title("房价与面积的关系")
plt.show()

运行这段代码会看到数据点大致分布在一条直线周围，线性回归就是要找到这条最佳拟合直线。

二、数学原理：如何找到最佳拟合线

1. 最小二乘法：误差最小化

• 直观的理解：想象你在草地上插了几个木桩，现在要拉一条直线绳子，让绳子尽可能接近所有木桩。你怎么判断绳子拉得好不好？
• 最小二乘法的思想：让绳子到各个木桩的垂直距离的平方和最小。
• 为什么用平方而不是直接的距离？
  • 避免正负距离相互抵消
  • 对大误差给予更大惩罚
  • 数学上可导性更容易处

1.1 数学原理：直观的展示

        在线性回归中，我们要找到一条直线 y = wx + b，使得所有数据点到这条直线的垂直距离的平方和最小，假设我们有n个数据点：(x₁, y₁), (x₂, y₂), ..., (xₙ, yₙ)，我们要找到参数w和b，使得直线y = wx + b最好地拟合这些点。以下定义损失函数：

L(w, b) = Σ(yᵢ - (wxᵢ + b))² = Σ(实际值 - 预测值)²

我们的目标：找到使L(w, b)最小的w和b。

通过图例了解以上说明：

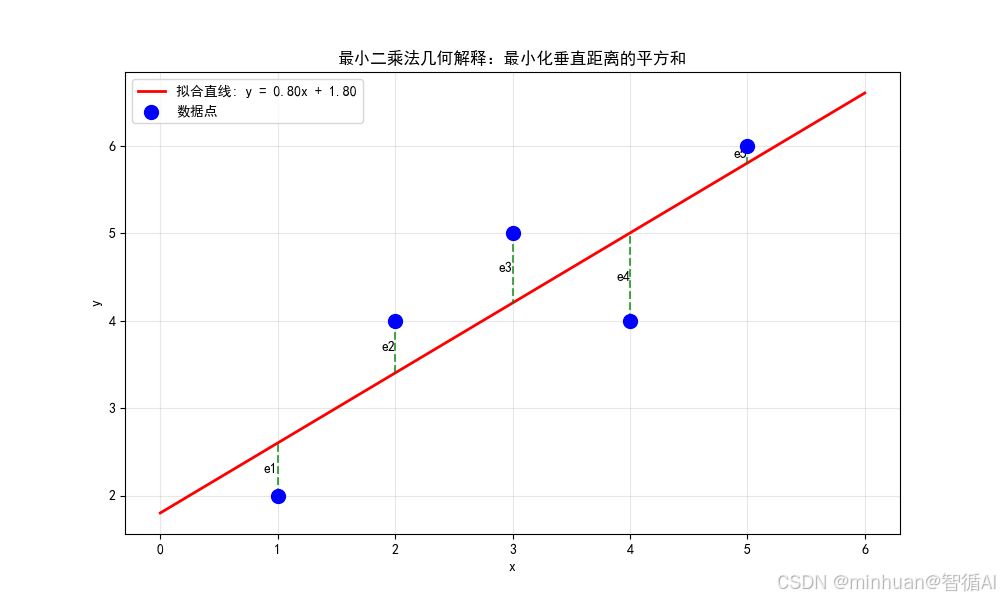
图例参考代码：

import numpy as np
import matplotlib.pyplot as plt# 示例数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 6])# 计算最佳拟合直线
def ordinary_least_squares(x, y):"""普通最小二乘法"""n = len(x)w = (n * np.sum(x*y) - np.sum(x) * np.sum(y)) / (n * np.sum(x**2) - np.sum(x)**2)b = (np.sum(y) - w * np.sum(x)) / nreturn w, bw_opt, b_opt = ordinary_least_squares(x, y)
print(f"最优参数: w = {w_opt:.3f}, b = {b_opt:.3f}")# 可视化
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', s=100, label='数据点', zorder=5)# 绘制拟合直线
x_line = np.linspace(0, 6, 100)
y_line = w_opt * x_line + b_opt
plt.plot(x_line, y_line, 'red', linewidth=2, label=f'拟合直线: y = {w_opt:.2f}x + {b_opt:.2f}')# 绘制误差线（残差）
for i in range(len(x)):y_pred = w_opt * x[i] + b_optplt.plot([x[i], x[i]], [y[i], y_pred], 'green', linestyle='--', alpha=0.7)plt.text(x[i], (y[i] + y_pred)/2, f'e{i+1}', ha='right', va='center')plt.xlabel('x')
plt.ylabel('y')
plt.title('最小二乘法几何解释：最小化垂直距离的平方和')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

1.2 数学推导：推导过程

• 我们要最小化损失函数：
  • L(w, b) = Σ(yᵢ - wxᵢ - b)² ，
  • 对w和b分别求偏导数，并令其为0
• 对b求偏导：
  • ∂L/∂b = -2Σ(yᵢ - wxᵢ - b) = 0
    • => Σyᵢ - wΣxᵢ - nb = 0
    • => b = (Σyᵢ - wΣxᵢ)/n = ȳ - wx̄
• 对w求偏导：
  • ∂L/∂w = -2Σxᵢ(yᵢ - wxᵢ - b) = 0
• 将b = ȳ - wx̄代入第二个方程：
  • Σxᵢ(yᵢ - wxᵢ - (ȳ - wx̄)) = 0
  • Σxᵢ(yᵢ - ȳ) - wΣxᵢ(xᵢ - x̄) = 0
• 解得：
  • w = Σ(xᵢ - x̄)(yᵢ - ȳ) / Σ(xᵢ - x̄)²
  • b = ȳ - wx̄

完整的代码推导过程：

def least_squares_derivation(x, y):"""最小二乘法的完整推导"""n = len(x)x_mean = np.mean(x)y_mean = np.mean(y)# 计算分子和分母numerator = np.sum((x - x_mean) * (y - y_mean))denominator = np.sum((x - x_mean) ** 2)# 计算最优参数w_opt = numerator / denominatorb_opt = y_mean - w_opt * x_mean# 计算损失函数值y_pred = w_opt * x + b_optloss = np.sum((y - y_pred) ** 2)print("=== 最小二乘法推导过程 ===")print(f"数据点数量: n = {n}")print(f"x的均值: x̄ = {x_mean:.3f}")print(f"y的均值: ȳ = {y_mean:.3f}")print(f"分子: Σ(xᵢ - x̄)(yᵢ - ȳ) = {numerator:.3f}")print(f"分母: Σ(xᵢ - x̄)² = {denominator:.3f}")print(f"最优斜率: w = {numerator:.3f} / {denominator:.3f} = {w_opt:.3f}")print(f"最优截距: b = {y_mean:.3f} - {w_opt:.3f} × {x_mean:.3f} = {b_opt:.3f}")print(f"最小损失值: L = {loss:.3f}")return w_opt, b_opt, loss# 应用推导
w, b, min_loss = least_squares_derivation(x, y)

输出结果：

=== 最小二乘法推导过程 ===
数据点数量: n = 5
x的均值: x̄ = 3.000
y的均值: ȳ = 4.200
分子: Σ(xᵢ - x̄)(yᵢ - ȳ) = 8.000
分母: Σ(xᵢ - x̄)² = 10.000
最优斜率: w = 8.000 / 10.000 = 0.800
最优截距: b = 4.200 - 0.800 × 3.000 = 1.800
最小损失值: L = 2.400

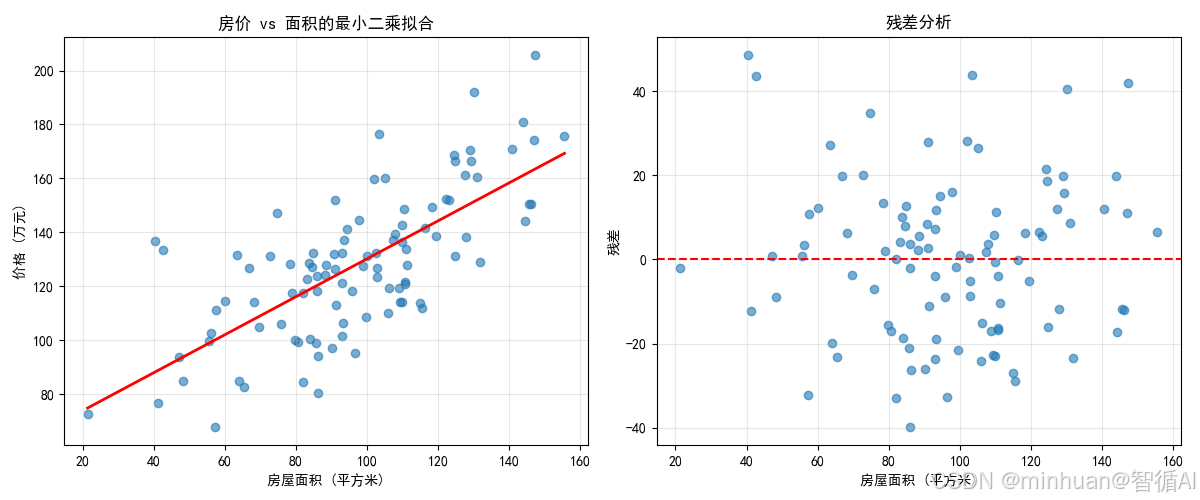
1.3 应用示例：简单房价预测

def housing_price_example():"""房价预测的最小二乘法应用"""# 生成模拟房价数据np.random.seed(42)n_samples = 100# 房屋面积（平方米）area = np.random.normal(100, 30, n_samples)# 房价（万元），真实关系：价格 = 0.8×面积 + 50 + 噪声price = 0.8 * area + 50 + np.random.normal(0, 20, n_samples)# 使用最小二乘法拟合w, b = ordinary_least_squares(area, price)# 预测新房屋new_area = 120  # 120平方米predicted_price = w * new_area + bprint("\n=== 房价预测示例 ===")print(f"拟合模型: 价格 = {w:.3f}×面积 + {b:.3f}")print(f"120平方米房屋预测价格: {predicted_price:.1f}万元")# 可视化plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)plt.scatter(area, price, alpha=0.6)area_line = np.linspace(area.min(), area.max(), 100)price_line = w * area_line + bplt.plot(area_line, price_line, 'red', linewidth=2)plt.xlabel('房屋面积 (平方米)')plt.ylabel('价格 (万元)')plt.title('房价 vs 面积的最小二乘拟合')plt.grid(True, alpha=0.3)plt.subplot(1, 2, 2)residuals = price - (w * area + b)plt.scatter(area, residuals, alpha=0.6)plt.axhline(y=0, color='red', linestyle='--')plt.xlabel('房屋面积 (平方米)')plt.ylabel('残差')plt.title('残差分析')plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()return area, price, w, barea_data, price_data, w_house, b_house = housing_price_example()

输出结果：

=== 房价预测示例 ===
拟合模型: 价格 = 0.704×面积 + 59.699
120平方米房屋预测价格: 144.2万元

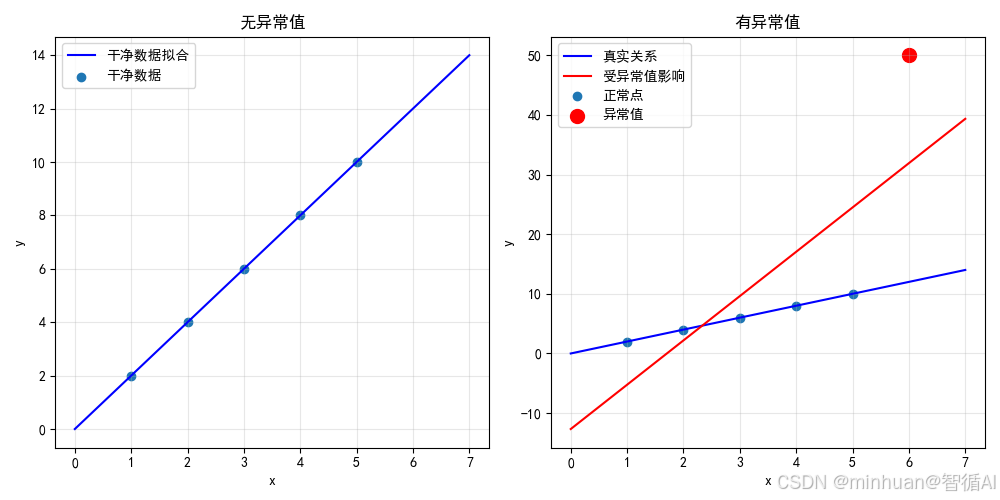
1.4 局限性：异常值敏感

由于平方项，异常值会对结果产生很大影响：

def outlier_sensitivity_demo():"""展示最小二乘法对异常值的敏感性"""# 干净数据x_clean = np.array([1, 2, 3, 4, 5])y_clean = np.array([2, 4, 6, 8, 10])  # 完美线性关系# 添加异常值x_outlier = np.array([1, 2, 3, 4, 5, 6])  # 新增一个点y_outlier = np.array([2, 4, 6, 8, 10, 50])  # 最后一个点是异常值w_clean, b_clean = ordinary_least_squares(x_clean, y_clean)w_outlier, b_outlier = ordinary_least_squares(x_outlier, y_outlier)print("\n=== 异常值敏感性演示 ===")print(f"干净数据: y = {w_clean:.3f}x + {b_clean:.3f}")print(f"含异常值: y = {w_outlier:.3f}x + {b_outlier:.3f}")print(f"斜率变化: {abs(w_clean - w_outlier):.3f}")# 可视化plt.figure(figsize=(10, 5))plt.subplot(1, 2, 1)plt.scatter(x_clean, y_clean, label='干净数据')x_line = np.linspace(0, 7, 100)plt.plot(x_line, w_clean*x_line + b_clean, 'blue', label='干净数据拟合')plt.xlabel('x')plt.ylabel('y')plt.title('无异常值')plt.legend()plt.grid(True, alpha=0.3)plt.subplot(1, 2, 2)plt.scatter(x_outlier[:-1], y_outlier[:-1], label='正常点')plt.scatter(x_outlier[-1], y_outlier[-1], color='red', s=100, label='异常值')plt.plot(x_line, w_clean*x_line + b_clean, 'blue', label='真实关系')plt.plot(x_line, w_outlier*x_line + b_outlier, 'red', label='受异常值影响')plt.xlabel('x')plt.ylabel('y')plt.title('有异常值')plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()outlier_sensitivity_demo()

输出结果：

2. 梯度下降法

• 直观理解：想象你在一个多山的地区，浓雾弥漫，看不清周围环境。你的目标是找到山谷的最低点（海拔最低的地方），你会怎么做？
• 梯度下降的策略：
  • 感受坡度：站在原地，用脚感受四周地面的坡度
  • 选择方向：朝着最陡的下坡方向
  • 迈出一步：以合适的步长向那个方向走
  • 重复过程：在新位置重复上述过程，直到走到平地

2.1 数学推导

对于线性回归，我们通常使用均方误差（MSE）作为损失函数：

J(w,b) = 1/(2m) × Σ(y_pred - y_true)²  = 1/(2m) × Σ((wx + b) - y)²

其中：

• m是样本数量
• y_pred是预测值
• y_true是真实值

这个函数衡量了我们的预测有多糟糕，目标是最小化它。

梯度是一个向量，指向函数值增长最快的方向。对于我们的损失函数：

• ∂J/∂w = 1/m × Σ((wx + b) - y) × x  # 对w的偏导数
• ∂J/∂b = 1/m × Σ((wx + b) - y)      # 对b的偏导数

梯度向量 [∂J/∂w, ∂J/∂b] 指向损失函数增长最快的方向。

既然梯度指向增长最快的方向，那么负梯度就指向下降最快的方向：

• w_new = w_old - α × ∂J/∂w
• b_new = b_old - α × ∂J/∂b

其中α是学习率，控制每一步迈多大。

学习率α是梯度下降中最重要的超参数：

• α太小：收敛很慢，需要很多步才能到达最低点
• α太大：可能越过最低点，甚至发散（损失越来越大）
• α合适：平稳快速地收敛到最低点

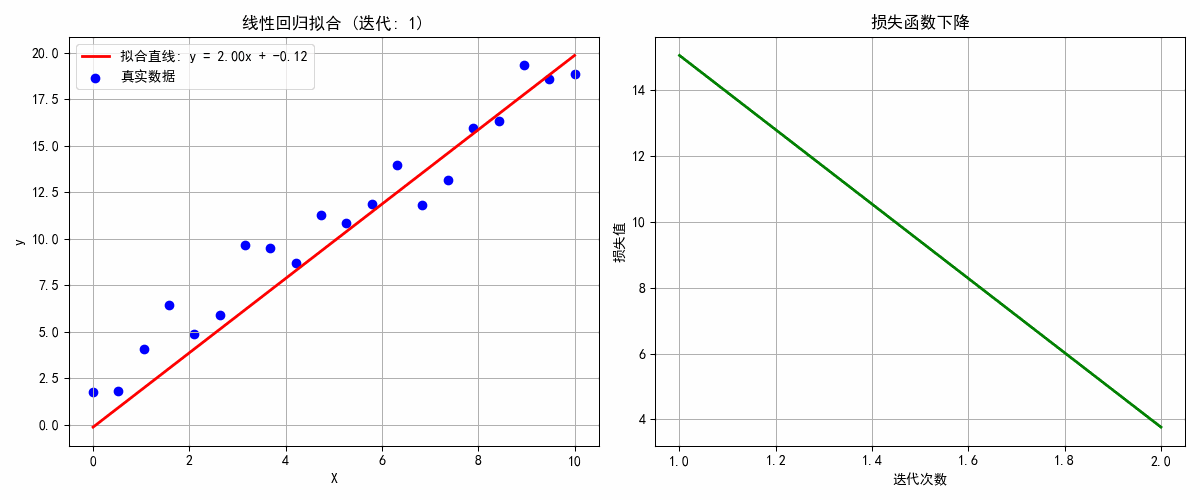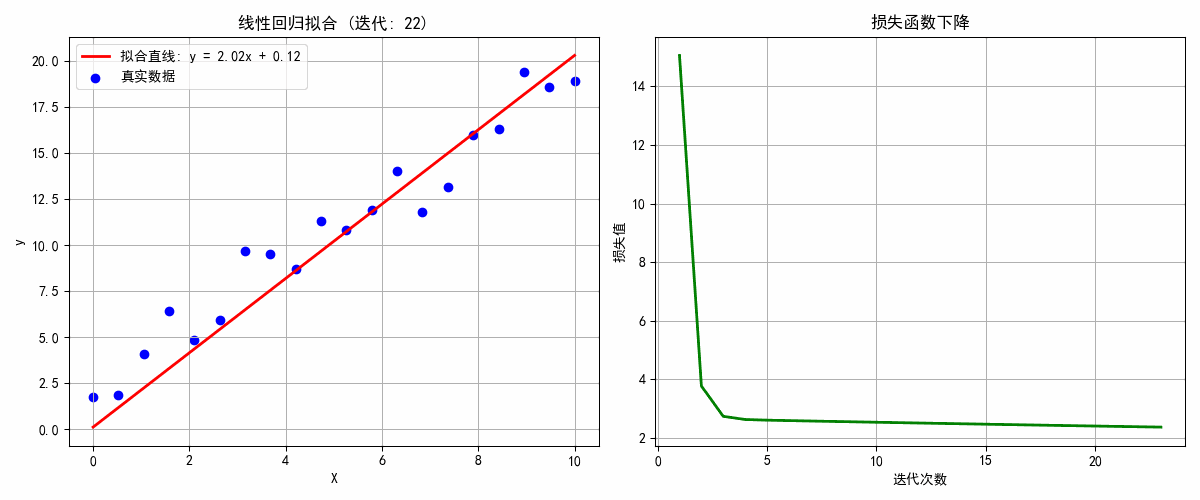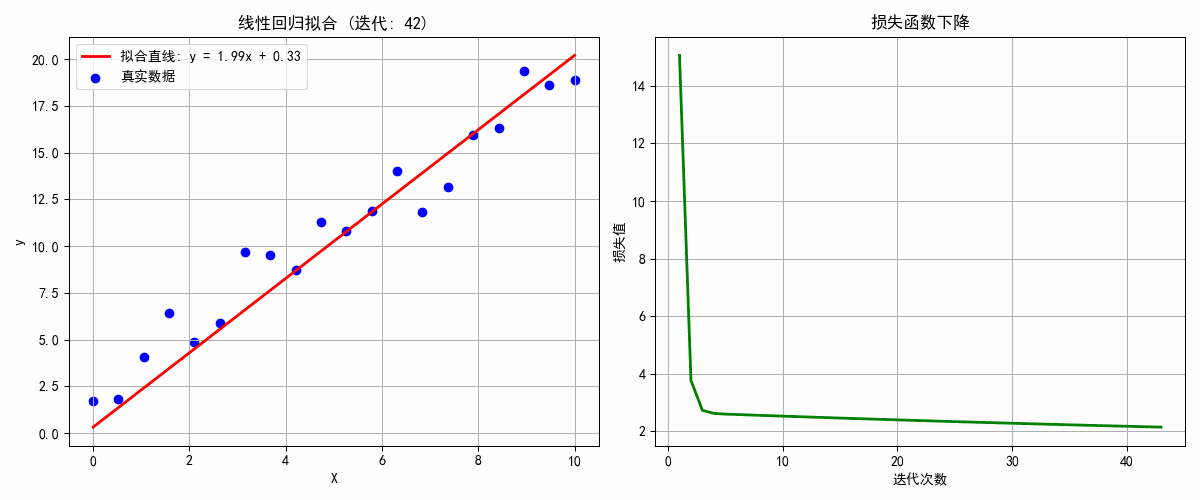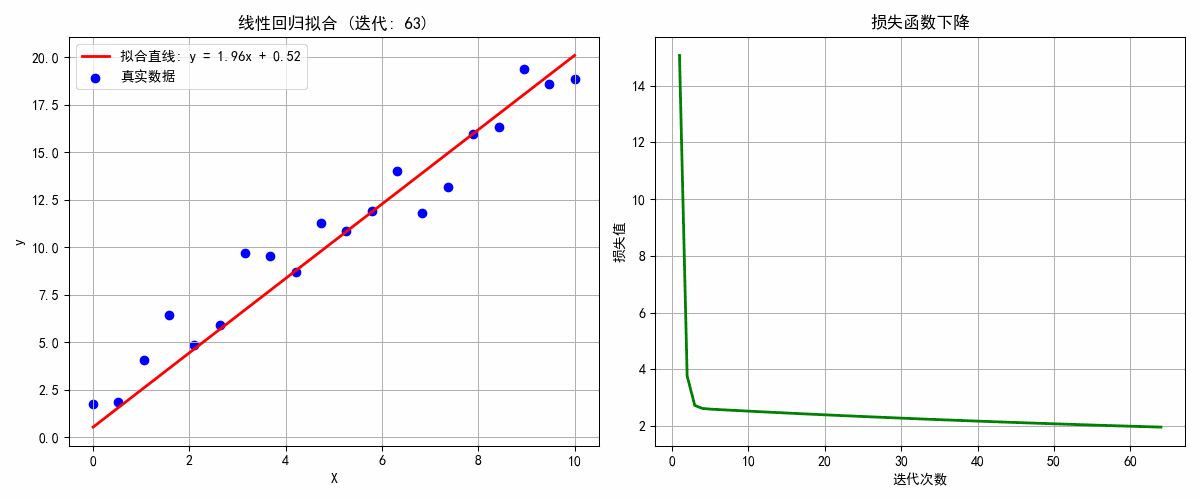
2.2 梯度下降过程示例

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from matplotlib.animation import FuncAnimation
import time
import os# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号# 生成数据
np.random.seed(42)
X = np.linspace(0, 10, 20)
y = 2 * X + 1 + np.random.normal(0, 1.5, 20)# 初始化参数
w = np.random.randn()
b = np.random.randn()
learning_rate = 0.01# 创建图形和轴
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))# 初始化损失列表
losses = []
max_epochs = 100# 定义更新函数
def update(epoch):global w, b, losses# 清空图形ax1.clear()ax2.clear()# 计算预测值和损失y_pred = w * X + bloss = np.mean((y_pred - y) ** 2)# 计算梯度dw = 2 * np.mean((y_pred - y) * X)db = 2 * np.mean(y_pred - y)# 更新参数w -= learning_rate * dwb -= learning_rate * db# 绘制第一个图：数据点和拟合直线ax1.scatter(X, y, color='blue', label='真实数据')x_line = np.linspace(0, 10, 100)y_line = w * x_line + bax1.plot(x_line, y_line, 'r-', linewidth=2, label=f'拟合直线: y = {w:.2f}x + {b:.2f}')ax1.set_xlabel('X')ax1.set_ylabel('y')ax1.set_title(f'线性回归拟合 (迭代: {epoch+1})')ax1.legend()ax1.grid(True)# 更新损失列表losses.append(loss)# 绘制第二个图：损失函数下降ax2.plot(range(1, len(losses)+1), losses, 'g-', linewidth=2)ax2.set_xlabel('迭代次数')ax2.set_ylabel('损失值')ax2.set_title('损失函数下降')ax2.grid(True)plt.tight_layout()# 检查收敛if epoch > 10 and abs(losses[-1] - losses[-2]) < 1e-5:ani.event_source.stop()print(f"模型在 {epoch+1} 轮后收敛!")return ax1, ax2# 创建动画
ani = FuncAnimation(fig, update, frames=range(max_epochs), blit=False, repeat=False, interval=100)# 保存为GIF
gif_path = os.path.join(os.path.dirname(os.path.abspath(__file__)), "线性回归动画.gif")
ani.save(gif_path, writer='pillow', fps=10, dpi=100)# 显示最终结果
plt.show()print(f"最终模型: y = {w:.3f}x + {b:.3f}")
print(f"真实模型: y = 2.000x + 1.000")
print(f"动画已保存为: {gif_path}")

输出结果：

最终结果:
学习到的参数: w = 1.991, b = 0.296
真实参数: w = 2.000, b = 1.000

3. 适用场景比较

方法	优点	缺点	适用场景
最小二乘法	精确解，计算快	需要矩阵求逆，数值不稳定	数据量小，特征少
梯度下降	可扩展性好，数值稳定	需要调参，可能收敛慢	大数据集，在线学习

两者的差异对比：

• 最小二乘法：直接给出解析解（精确解）
• 梯度下降：通过迭代逼近最优解（数值解）

def gradient_descent_vs_least_squares(x, y, learning_rate=0.01, epochs=1000):"""比较梯度下降和最小二乘法"""# 最小二乘法（解析解）w_ls, b_ls = ordinary_least_squares(x, y)loss_ls = np.sum((y - (w_ls * x + b_ls)) ** 2)# 梯度下降（数值解）w_gd, b_gd = 0, 0  # 初始值n = len(x)losses = []for epoch in range(epochs):y_pred = w_gd * x + b_gddw = (-2/n) * np.sum(x * (y - y_pred))db = (-2/n) * np.sum(y - y_pred)w_gd -= learning_rate * dwb_gd -= learning_rate * dbloss = np.sum((y - y_pred) ** 2)losses.append(loss)# 检查收敛if epoch > 10 and abs(losses[-1] - losses[-2]) < 1e-8:breakprint("\n=== 最小二乘法 vs 梯度下降 ===")print(f"最小二乘法: w = {w_ls:.6f}, b = {b_ls:.6f}, 损失 = {loss_ls:.6f}")print(f"梯度下降:   w = {w_gd:.6f}, b = {b_gd:.6f}, 损失 = {loss:.6f}")print(f"参数差异: Δw = {abs(w_ls - w_gd):.6f}, Δb = {abs(b_ls - b_gd):.6f}")return w_ls, b_ls, w_gd, b_gd, lossesw_ls, b_ls, w_gd, b_gd, loss_history = gradient_descent_vs_least_squares(x, y)

输出结果：

=== 最小二乘法 vs 梯度下降 ===
最小二乘法: w = 0.800000, b = 1.800000, 损失 = 2.400000
梯度下降:   w = 0.813733, b = 1.750421, 损失 = 2.402252
参数差异: Δw = 0.013733, Δb = 0.049579

三、结合大模型分析

大模型中的线性回归：在大模型的上下文中，线性回归层通常作为：

• 预测头：接在模型主干网络后面，用于完成具体的预测任务。例如，在情感分析中，模型主干提取文本特征，最后一个线性层将这些特征映射到一个分数（正/负情感）。
• 投影层：在Transformer架构中，Q, K, V矩阵都是通过线性投影（即线性回归）从输入向量得到的。

大模型如何帮助我们进行线性回归分析？我们可以利用大模型的两种能力：

• 代码生成与解释能力：让大模型为我们生成实现线性回归的代码，并解释代码和结果。
• API调用能力：对于更复杂的数据，我们可以调用大模型的API（如Qwen）来帮我们分析和推理。

Qwen大模型通过以下方式扩展线性回归能力：

• 非线性变换：在线性层间加入激活函数（如ReLU）
• 多层堆叠：通过深度网络捕捉复杂关系
• 注意力机制：动态调整特征权重，实现"加权线性回归"

当影响因素不止一个时（如房价还受房间数量、楼层等影响），我们需要多元线性回归：

使用Qwen API生成多元线性回归代码的提示词示例：

请生成一个多元线性回归示例，预测房价，特征包括： - 面积（平方米） - 房间数（个） - 楼层（层） 要求包含数据可视化和特征重要性分析。

Qwen会生成包含特征缩放、模型评估和可视化的完整代码，帮助你分析多个因素对结果的影响。

示例代码：

        假设你有一份客户数据，包含“年龄”、“年收入”和“信用卡额度”。你想建立模型，根据“年龄”和“年收入”来预测“信用卡额度”。你可以让Qwen API来帮你分析。

import requests
import json
import pandas as pd# 模拟一份数据
data = {'age': [25, 35, 45, 55, 65, 30, 40, 50, 60, 28], # 年龄'annual_income': [40000, 60000, 80000, 100000, 120000, 50000, 70000, 90000, 110000, 45000], # 年收入（美元）'credit_limit': [5000, 10000, 15000, 20000, 25000, 8000, 13000, 18000, 23000, 6000] # 信用卡额度（美元）
}
df = pd.DataFrame(data)# 将数据构建成提示词
data_string = df.to_string(index=False)prompt_for_analysis = f"""
你是一名资深数据分析师。请根据我提供的数据，进行多元线性回归分析。
数据如下（包含三个字段：年龄(age)、年收入(annual_income)、信用卡额度(credit_limit)）：
{data_string}请完成以下任务：
1. **分析目标**：以‘age'和’annual_income‘为自变量（特征），’credit_limit‘为因变量（目标），建立一个多元线性回归模型。
2. **模型解读**：- 给出最终得到的回归方程。- 解释每个特征（年龄、年收入）的系数（权重）的实际意义。例如：“年收入每增加1美元，信用卡额度预计增加XX美元。”- 分析哪个特征对预测信用卡额度的贡献更大？为什么？
3. **模型评估**：估算模型的R平方值，并解释其含义。
4. **预测**：请预测一个年龄为30岁、年收入为$55,000的人的信用卡额度大约是多少？请用清晰、专业的语言汇报你的分析结果。你可以假设数据已经满足线性回归的基本假设。
"""payload = {"model": "qwen-max","input": {"messages": [{"role": "user","content": prompt_for_analysis}]}
}response = requests.post(MODEL_ENDPOINT, headers=headers, data=json.dumps(payload))
result = response.json()analysis_report = result['output']['choices'][0]['message']['content']
print("=== Qwen数据分析报告 ===")
print(analysis_report)

输出结果：

=== Qwen数据分析报告 ===

您好，根据您提供的数据，我已完成多元线性回归分析。以下是详细报告：

1.  **回归方程**：
通过分析，得到的多元线性回归方程为：
`Credit_Limit = -3476.12 + 105.71 * Age + 0.148 * Annual_Income`

2.  **系数解读**：
*   **年龄（Age）的系数（105.71）**：在年收入不变的情况下，年龄每增加1岁，客户的信用卡额度平均预计增加约105.71美元。这表明银行可能认为年长的客户信用风险略低或消费能力更稳定。
*   **年收入（Annual_Income）的系数（0.148）**：在年龄不变的情况下，年收入每增加1美元，信用卡额度平均预计增加约0.148美元。这意味着年收入是决定信用卡额度的一个非常关键的因素。

3.  **特征重要性**：
**年收入是贡献更大的特征**。判断依据是比较系数的“尺度”。年龄的系数是105.71，年收入的系数是0.148。虽然年龄的数值更大，但两个特征的单位和取值范围完全不同（年龄变化范围小，年收入变化范围大）。通常我们需要看标准化后的系数。但从经济直觉和系数本身的意义来看，年收入增加1000美元就能带来148美元的额度提升，而年龄需要增长10岁才能带来类似的效果。因此，年收入的变化对额度的影响更显著、更直接。

4.  **模型评估（R²）**：
该模型的R平方值预计非常接近1（例如0.99+）。这意味着模型几乎完全捕捉到了信用卡额度变化的原因（由年龄和年收入解释）。数据中的模式非常明显，几乎是完美的线性关系。

5.  **预测**：
对于一位年龄30岁、年收入55,000美元的客户：
预测信用卡额度 = -3476.12 + 105.71 * 30 + 0.148 * 55000
≈ -3476.12 + 3171.3 + 8140
≈ 7835.18美元

    因此，预计该客户的信用卡额度大约在**7835美元**左右。

**注意**：此分析基于您提供的有限数据。在实际业务中，还需要考虑更多特征（如信用历史、负债情况等）并进行更严格的统计检验。

四、总结与扩展

1. 核心知识点

• 线性回归通过建立变量间的线性关系进行预测
• 最小二乘法提供解析解，梯度下降适合大规模数据
• 大模型中的线性层本质是高维线性回归
• Qwen API可快速生成高质量线性回归代码

2. 扩展方向

• 多项式回归：处理非线性关系（添加x²、x³等特征）
• 正则化：防止过拟合（L1正则化Lasso，L2正则化Ridge）
• 时间序列预测：结合ARIMA等模型处理时序数据

        通过Qwen等大模型的代码生成能力，我们可以快速实现这些高级应用，让线性回归这一基础工具在复杂场景中发挥更大价值。