ADMM 算法的基本概念

        ADMM是一种分布式优化方法，其主要思想为将复杂的目标问题进行分解，得到多个可以并行求解的子问题，在对优化问题进行求解的过程中，先对每个子问题进行局部优化求解，最后将局部子问题的最优解进行融合得到全局问题的最优解。其算法模型为：

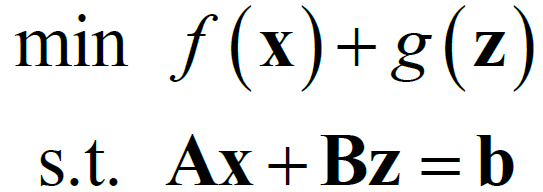
        其中，，函数和为关于变量x和z的连续函数。由上述模型可以看出，ADMM算法的全局变量可以拆分成两个可分离的局部变量，且这两个局部变量满足约束条件中的线性等式约束，同时目标函数关于这两个局部变量也可拆分成两个可分离的子函数。
ADMM 对于函数f 和g 的凸性没有要求，函数f 和g 为凸函数或者非凸函数，ADMM都可以进行求解。增广拉格朗日函数可以写成如下形式：

        其中，y 为拉格朗日乘子，称为惩罚因子，ADMM 算法的迭代过程可以分成三步：

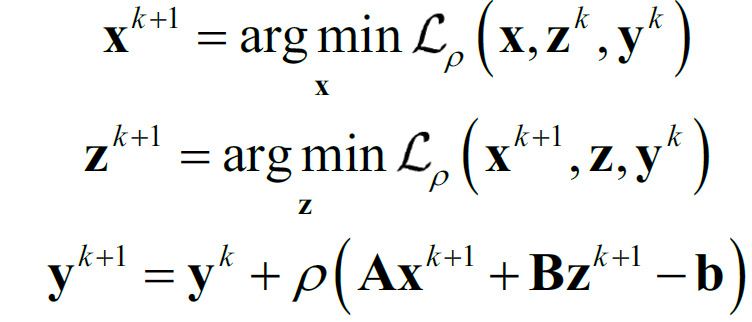
        由上述公式可以看出，ADMM 算法首先利用上一次迭代的变量z 和拉格朗日乘子y更新变量x ，之后利用刚更新的局部变量x 和上一次迭代的拉格朗日乘子y 更新局部变量z ，最后根据在本次迭代中已经更新的局部变量x 和z 来更新拉格朗日乘子y 。
按照这样的顺序，ADMM 算法的各个变量之间交替更新。为了简化形式，定义，可以将ADMM 算法的迭代过程写成放缩的形式：

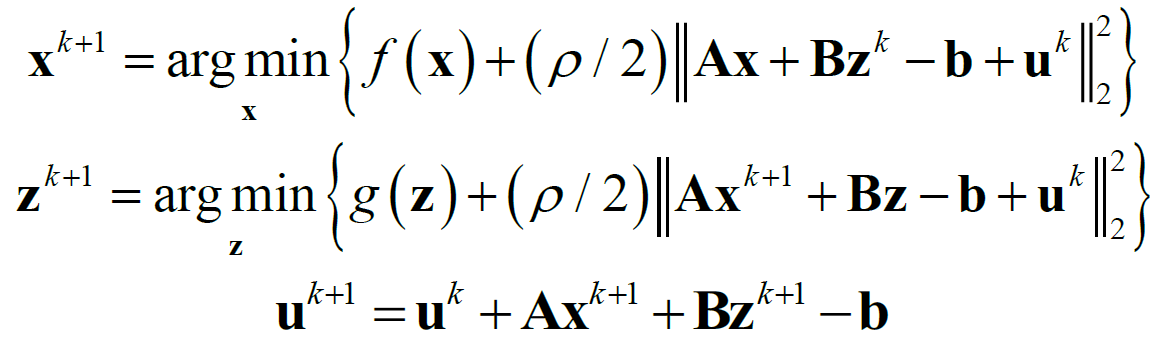
        这里定义对偶残差 和原始残差。一般来说，ADMM 算法迭代的终止准则可以通过原始残差和对偶残差来判断，当原始残差和对偶残差足够小时，即

        ADMM 算法迭代过程可以终止，其中和为原始可行条件和对偶可行条件的容忍度。