施工企业负责人seo关键词排名优化怎样收费

数学建模层次分析法（AHP）笔记

一、算法简介

1. 定义

层次分析法（Analytic Hierarchy Process，简称AHP）是美国运筹学家萨蒂（T. L. Saaty）于20世纪70年代提出的一种多层次权重决策分析方法，旨在解决多目标、多准则的复杂决策问题。

2. 核心思想

• 将定性分析与定量计算结合，通过决策者的经验判断各因素的相对重要性。
• 将复杂问题分解为多层次结构，逐层计算权重，最终得到方案的优劣排序。

3. 适用场景

• 难以用纯定量方法解决的决策问题（如资源分配、方案选择、绩效评价等）。
• 需考虑多个相互关联、相互制约的因素的场景。

二、基本原理与步骤

1. 解决问题的思路

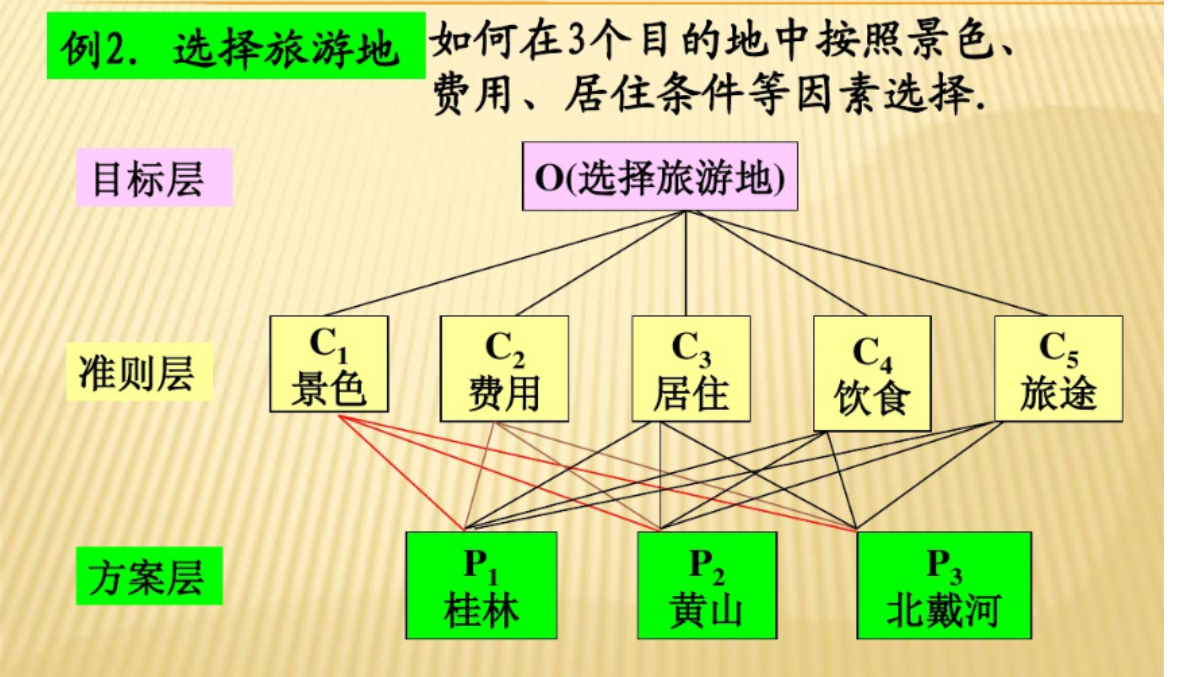
（示意图说明：将问题分解为“目标层-准则层-方案层”的多层次结构，通过逐层计算权重实现决策）

2. 具体步骤

步骤1：建立层次结构模型

• 最高层（目标层）：决策的最终目的（如“选择最优旅游目的地”）。
• 中间层（准则层）：影响目标实现的因素（如“景色、费用、交通、住宿”）。
• 最低层（方案层）：备选方案（如“桂林、北京、上海”）。

示例：

目标层：选择最佳旅游地
├─准则层：景色、费用、交通、住宿
│  ├─方案层：桂林
│  ├─方案层：北京
│  └─方案层：上海

步骤2：构造判断矩阵

• 核心：通过两两比较确定同一层次因素对上层因素的相对重要性，采用1-9标度法量化判断。

标度	含义
1	两因素同等重要
3	一因素比另一因素稍微重要
5	一因素比另一因素明显重要
7	一因素比另一因素强烈重要
9	一因素比另一因素极端重要
2,4,6,8	相邻标度的中值
倒数	若i比j为a，则j比i为1/a

示例：
若准则层为“景色（C1）、费用（C2）、交通（C3）”，构造目标层对准则层的判断矩阵如下：
$$A=\left[\begin{array}{ccc}1& 1/3& 2\\ 3& 1& 5\\ 1/2& 1/5& 1\end{array}\right]$$
（注：A[i][j]表示Ci与Cj的重要性比值）

步骤3：层次单排序及其一致性检验

• 层次单排序：计算判断矩阵的最大特征根λ_max及其对应的特征向量，归一化后即为该层次因素对上层因素的权重。
• 一致性检验：判断矩阵是否合理（避免逻辑矛盾）。

计算公式：

1. 一致性指标（CI）：
   $$CI=\frac{{\lambda }_{\text{max}}-n}{n-1}$$
   （n为判断矩阵阶数，CI=0表示完全一致）

2. 随机一致性指标（RI）：（查表可得）

   n	1	2	3	4	5	6	7	8	9	10	11
   RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49	1.51

3. 一致性比率（CR）：
   $$CR=\frac{CI}{RI}$$

   • 若CR < 0.1，判断矩阵通过一致性检验；
   • 否则需调整判断矩阵。

示例：
对步骤2中的矩阵A，计算得λ_max≈3.005，n=3：
$$CI=\frac{3.005-3}{3-1}=0.0025$$
$$CR=\frac{0.0025}{0.58}\approx 0.004<0.1$$
→ 通过一致性检验，归一化特征向量即为准则层权重。

步骤4：层次总排序及其一致性检验

• 层次总排序：计算最底层（方案层）对最高层（目标层）的总权重，公式为：
  $$\text{总权重}=\sum _{j=1}^m{a}_j\cdot b_{ij}$$
  （a_j为上层因素权重，b_ij为下层因素对上层第j个因素的权重）

• 总排序一致性检验：
  $$C{R}_{\text{总}}=\frac{{\sum }_{j=1}^m{a}_j\cdot C{I}_j}{{\sum }_{j=1}^m{a}_j\cdot R{I}_j}$$
  （CR总 < 0.1则通过检验）

示例：
若准则层权重为[0.23, 0.64, 0.13]，方案层对各准则的权重如下表，则总排序为：

方案	景色（0.23）	费用（0.64）	交通（0.13）	总权重
桂林	0.45	0.20	0.50	0.23×0.45 + 0.64×0.20 + 0.13×0.50 ≈ 0.28
北京	0.40	0.35	0.30	0.36
上海	0.15	0.45	0.20	0.36

→ 方案排序：北京=上海 > 桂林。

三、算法总结

1. 应用领域

• 经济管理（资源分配、投资决策）、能源政策、人才评价、生产计划、科研选题等。

2. 优势与局限

• 优势：简单直观，融合定性与定量分析，适合复杂决策。
• 局限：依赖决策者主观判断，样本量较小时可能偏差较大。

3. 注意事项

• 层次结构模型需由决策专家参与设计，确保因素全面性。
• 判断矩阵的构造需经验丰富者填写，以保证合理性。

注：实际应用中可借助Python（如numpy计算特征值）或MATLAB实现AHP的自动化计算，提高效率。