机器学习——逻辑回归详解

一、逻辑回归简介

1.1 极大似然估计

1. 核心思想：根据观测到的结果来估计模型算法中的未知参数
2. Sigmoid函数：把数值映射到（0,1）：$\sigma (z)=\frac{1}{1+e^{-z}}$
3. 极大似然函数：概率密度的乘积

假设有概率密度：$$f(x;\mu )=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}(x-\mu {)}^2},-\infty <x<+\infty$$
那么其似然函数为：$$L=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(x_i-\mu \right)}^2}=\frac{1}{{\left(\sqrt{2\pi }\right)}^n}\exp \left\{-\frac{1}{2}\sum _{i=1}^n{\left(x_i-\mu \right)}^2\right\}$$
现在希望求得什么$\mu$为何值时似然函数最大，由于乘法难以运算，因此可以同时取对数
对似然函数两边同时取ln：$$\ln L=-\frac{n}{2}\ln \left(2\pi \right)-\frac{1}{2}\sum _{i=1}^n{\left(x_i-\mu \right)}^2$$
对参数$\mu$求导函数：$$\frac{d\ln L}{d\mu }=\sum _{i=1}^n(x_i-\mu )=0$$因此当$x=\mu$时，概率最大，$\mu$为x的均值：$$\hat{\mu }=\frac{1}{n}\sum _{i=1}^n{x}_i=\overline{x}$$

1.2 逻辑回归原理

1. 概念：一种分类模型，把线性回归的输出，作为逻辑回归的输入

为什么逻辑回归的输入是线性回归的输出？
如果将逻辑回归比作法官判定犯人是否有罪，那么线性回归就是判定前收集“证据”的那一部分
事实上，逻辑回归的输入是线性回归的输出，是因为我们需要一个能够衡量“证据”强弱的连续值，然后再将这个“证据”值转化为一个概率
分类问题的本质是找到一条“边界”，将不同类别的数据点分开
线性回归$z=w^{T}x+b$本身就能定义一个边界（即 z = 0 的超平面）。在二维图上，这就是一条直线。这条直线的一边是 z > 0，另一边是 z < 0，逻辑回归直接利用了线性回归的这个强大能力来寻找决策边界

2. 基本思想：

• 利用线性回归模型$f(x)=w^{T}x+b$根据特征的重要性计算出一个值
• 再利用Sigmoid函数将f(x)的输出值映射为概率值：$h(w)=sigmoid(w^{T}x+b)$

3. 损失函数：$\mathrm{Loss}(\mathrm{L})=-{\sum }_{i=1}^m(y_i\log (p_i)+(1-y_i)\log (1-p_i))$

推导：给定一个输入特征 x，模型需要输出一个概率值，表示属于正类（通常标记为 1）的可能性
那么在x的情况下，将y标记为1的概率为：$$\hat{p}=P(y=1|x)=\sigma (w^{T}x+b)，其中\sigma (z)=\frac{1}{1+e^{-z}}$$
相应的，在x的情况下，将y标记为0的概率为：$$P(y=0|x)=1-\hat{p}$$ 对于一个训练样本 (x,y)，其真实标签 y 要么是 0，要么是 1，我们可以用一个巧妙的公式同时描述这两种情况：$$P(y|x)={\hat{p}}^y\cdot (1-\hat{p}{)}^{1-y}$$
现在我们推广至数量为m个独立的训练集，就可以得到他的似然函数为：$$L(w,b)=\prod _{i=1}^{m}P(y^{(i)}|x^{(i)})=\prod _{i=1}^m{\left({\hat{p}}^{(i)}\right)}^{y^{(i)}}{\left(1-{\hat{p}}^{(i)}\right)}^{1-y^{(i)}}$$
现在我们的目标是找到一个w，b使得L（w，b）最大，同样的，运算乘积十分麻烦，我们可以取对数：$$\ell (w,b)=\sum _{i=1}^m\left[y^{(i)}\log {\hat{p}}^{(i)}+(1-y^{(i)})\log (1-{\hat{p}}^{(i)})\right]$$
这样我们就得到了损失函数，而在机器学习中，我们希望损失函数越小越好，因此我们在这个公式前面加一个负号：$$J(w,b)=-\ell (w,b)=-\sum _{i=1}^m\left[y^{(i)}\log {\hat{p}}^{(i)}+(1-y^{(i)})\log (1-{\hat{p}}^{(i)})\right]$$

损失效果的例子： 你正在教一个小学生（我们的模型）做一道只有“对”和“错”两种答案的是非题

• 真实答案 (y)：就是标准答案。y=1 代表“对”，y=0 代表“错”
• 模型的信心 ( p )：代表小学生对“我的答案是对的吗？”这个问题的确信程度。p=1 表示他 100% 肯定自己答对了；p=0 表示他 100% 肯定自己答错了；p=0.6 表示他有点犹豫，但 60% 倾向于自己答对了
• 我们的目标是：让模型的信心尽可能地匹配真实答案

场景一：学生答对了题，并且他很自信（正确且自信）

• 真实答案 (y)：1 (“对”)
• 学生的信心 ( p )：0.9 (他90%确信自己答对了)
• 损失函数：$L=-[y\ast log(\hat{y})+(1-y)\ast log(1-\hat{y})]=-[1\ast log(0.9)+0]\approx -[log(0.9)]\approx -(-0.105)=0.105$
• 损失值很小（只有 0.105），这时你就可以对模型说：“嗯，你答对了，而且你很自信，这很好！只扣你一点点分，作为鼓励。”
• 这是一种奖励多于惩罚的状态

场景二：学生答对了题，但他非常犹豫（正确但不自信）

• 真实答案 (y)：1 (“对”)
• 学生的信心 ( p )：0.6 (他只有60%的把握，几乎是在猜)
• 损失函数：$L=-[1\ast log(0.6)]\approx -(-0.51)=0.51$
• 损失值变大了（0.51 > 0.105），这时你会对模型说说：“你虽然答对了，但你根本不确定，像是在蒙答案。这可不怎么样，我要多扣你一点分，让你下次要建立正确的信心！”
• 模型因此被惩罚，促使它以后在面对正确答案时要有更高的信心

场景三：学生答错了题，但他非常自信（错误且自信）

• 真实答案 (y)：0 (“错”)
• 学生的信心 ( p )：0.9 (他90%确信自己答对了，但实际上是错的)
• 损失函数：$L=-[0+(1-0)\ast log(1-0.9)]=-[log(0.1)]\approx -(-2.3)=2.3$
• 损失值变得非常大（2.3）！你严厉的批评了模型：“你完全答错了，还自以为是！这是最糟糕的情况，我要重重地罚你！”
• 这种巨大的惩罚会强烈地“敲打”模型，迫使它迅速调整参数，大幅降低对这种错误预测的信心

场景四：学生答错了题，他也很不确定（错误且不自信）

• 真实答案 (y)：0 (“错”)
• 学生的信心 ( p )：0.4 (他60%觉得自己错了，40%觉得自己对)
• 损失函数：$L=-[0+1\ast log(1-0.4)]=-[log(0.6)]\approx -(-0.51)=0.51$
• 损失值中等（0.51）。你对模型说：“你答错了，但好在你自己也不太确定。这比那些答错了还趾高气扬的要好一点，但还是得扣分，让你明白这是错的。”

二、逻辑回归

2.1 API

sklearn.linear model.LogisticRegression(solver='liblinear', penalty= '12' , C = 1.0)

1. liblinear对小数据集场景训练速度更快,sag和 saga 对大数据集更快一些。
2. 正则化:

• sag、saga支持L2正则化或者没有正则化
• liblinear 和 saga 支持L1正则化
• penalty:正则化的种类,11或者12
• C:正则化力度
• 默认将类别数量少的当做正例

2.2 案例

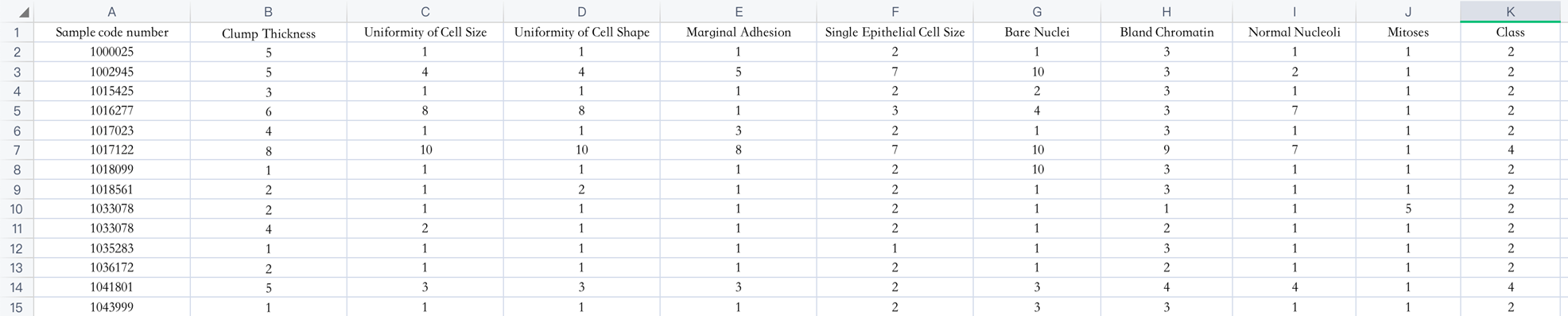
• 癌症分类案例，699条样本,共11列数据,第一列用语检索的id,后9列分别是与肿瘤相关的医学特征,最后一列表示肿瘤类型的数值
• 包含16个缺失值,用”?”标出
• 2表示良性,4表示恶性

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
import numpy as np
from sklearn.metrics import accuracy_scoredata = pd.read_csv("breast-cancer-wisconsin.csv")
data = data.replace(to_replace="?",value=np.nan)
data = data.dropna()
x = data.iloc[:, 1:-1]
y = data.iloc[:,-1]
x_train , x_test , y_train , y_test = train_test_split(x , y , test_size = 0.2 , random_state = 22)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
estimator = LogisticRegression()
estimator.fit(x_train , y_train)
y_pre = estimator.predict(x_test)
accuracy = accuracy_score(y_test, y_pre)
print(accuracy)

三、分类问题评估

3.1 混淆矩阵

• 注：伪反例往往比伪正例更严重，因此当模型准确率相同时，优先选择伪反例少的

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pre,labels=[0,1])

1. 精确率（查准率）：预测为正例中实际为正例的比例

• 计算方法：$P=\frac{TP}{TP+FP}$

rom sklearn.metrics import precision_score
precision_score(y_test, y_pre,pos_label=1)

2. 召回率（查全率）：实际为正例中被预测为正例的比例

• 计算方法：$P=\frac{TP}{TP+FN}$

from sklearn.metrics import recall_score
recall_score(y_test, y_pre,pos_label=1)

3. F1-score：精确率和召回率的调和平均数

• 计算方法：$P=\frac{2\ast Precision\ast Recall}{Precision+Recall}$

from sklearn.metrics import f1_score
f1_score(y_test, y_pre,pos_label=1)

3.2 ROC曲线和AUC指标

1. 真正率TPR：正样本中被预测为正样本的概率
2. 假正率FPR：负样本中被预测为正样本的概率
3. ROC曲线：是一种常用于评估分类模型性能的可视化工具。ROC曲线以模型的真正率TPR为纵轴，假正率FPR为横轴，它将模型在不同阈值下的表现以曲线的形式展现出来
4. AUC曲线下面积：ROC曲线的优劣可以通过曲线下的面积(AUC)来衡量，AUC越大表示分类器性能越好

• 当AUC=0.5时,表示分类器的性能等同于随机猜测
• 当AUC=1时,表示分类器的性能完美,能够完全正确地将正负例分类
  

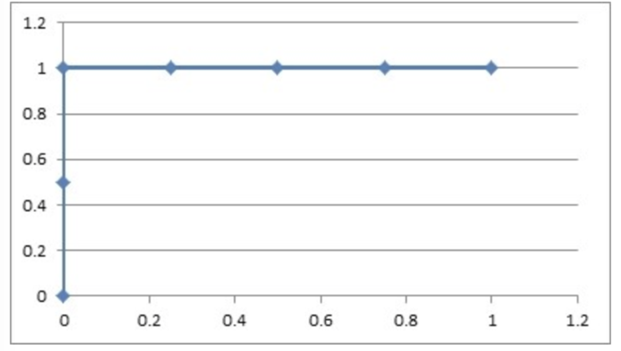
曲线越靠近(0,1)点则模型对正负样本的辨别能力就越强
AUC是ROC曲线下面的面积，该值越大，则模型的辨别能力就越强，AUC范围在[0,1]之间
当AUC=1时，该模型被认为是完美的分类器，但是几乎不存在完美分类器
当AUC <=0.5时，模型区分正负样本的就会变得模棱两可，近似于随机猜测

3.3 ROC与AUC案例

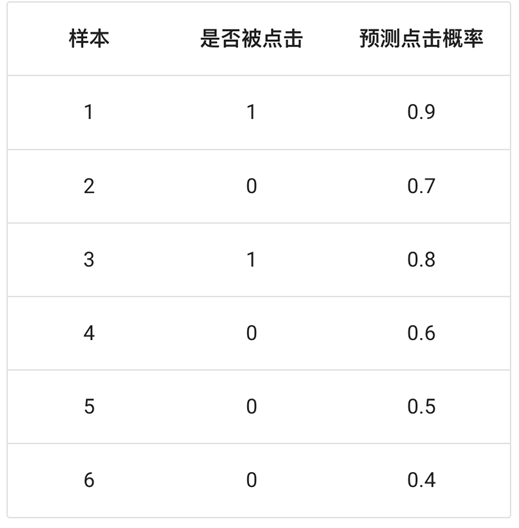
• 已知：在网页某个位置有一个广告图片，该广告共被展示了6次；有2次被浏览者点击了。其中正样本{1,3}，负样本为{2,4,5,6}；求在不同阈值下的ROC曲线
  

• 阈值：0.9

  • 原本为正例的1、3号的样本中3号样本被分类错误，则TPR=0/2=0
  • 原本为负例的2、4、5、6号样本没有一个被分为正例，则FPR=0
  • 曲线坐标：（0,0）

• 國值：0.8

  • 原本为正例的1、3号样本被分类正确，则TPR=1/2=0.5
  • 原本为负例的2、4、5、6号样本没有一个被分为正例，则FPR=0
  • 曲线坐标：（0,0.5）

• 國值:0.7

  • 原本为正例的1、3号样本被分类正确，则 TPR=2/2=1
  • 原本为负类的2、4、5、6号样本中2号样本被分类错误，则FPR=0/4=0
  • 曲线坐标：（0,1）

• 國值:0.6

  • 原本为正例的1、3号样本被分类正确，则TPR=2/2=1
  • 原本为负类的2、4、5、6号样本中2、4号样本被分类错误，则FPR=1/4=0.25
  • 曲线坐标：（0.25,1）

• 國值:0.5

  • 原本为正例的1、3号样本被分类正确，则TPR=2/2=1
  • 原本为负类的2、4、5、6号样本中2、4、5号样本被分类错误，则FPR=2/4=0.5
  • 曲线坐标：（0.5,1）

• 阈值0.4

  • 原本为正例的1、3号样本被分类正确，则TPR=2/2=1
  • 原本为负类的2、4、5、6号样本全部被分类错误，则FPR=3/4=0.75
  • 曲线坐标：（0.75,1）

四、电信客户流失预测案例

• 数据集churn有以上特征，我们需要通过一些特征预测客户是否会流失
• 由于Gender信息中存在“Male”和“Female”字段，逻辑回归时无法进行识别，因此需要将其转化为热编码，churn同理，存在“chunrn_Yes”与“chunrn_No”字段，因此可以去除“chunrn_No”字段，并修改“chunrn_Yes”为“flag”来简化数据集

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score , roc_auc_score , classification_reportdata = pd.read_csv("churn.csv")
data = pd.get_dummies(data)
data = data.drop(["Churn_No" , "gender_Male"] , axis=1)
data = data.rename(columns={"Churn_Yes" : "flag"})
sns.countplot(data=data , x = "Contract_Month" , hue="flag")
plt.show()
x = data[["PaymentElectronic" , "Contract_Month" , "internet_other"]]
y = data["flag"]
# 数据集划分
x_train , x_test , y_train , y_test = train_test_split(x , y , test_size = 0.2, random_state = 22)
# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 模型训练
estimator = LogisticRegression()
estimator.fit(x_train, y_train)
# 模型评估
y_pre = estimator.predict(x_test)
roc_auc_score = roc_auc_score(y_test, y_pre)
classification_report = classification_report(y_test, y_pre)print(accuracy_score(y_test, y_pre))
print(roc_auc_score)
print(classification_report)