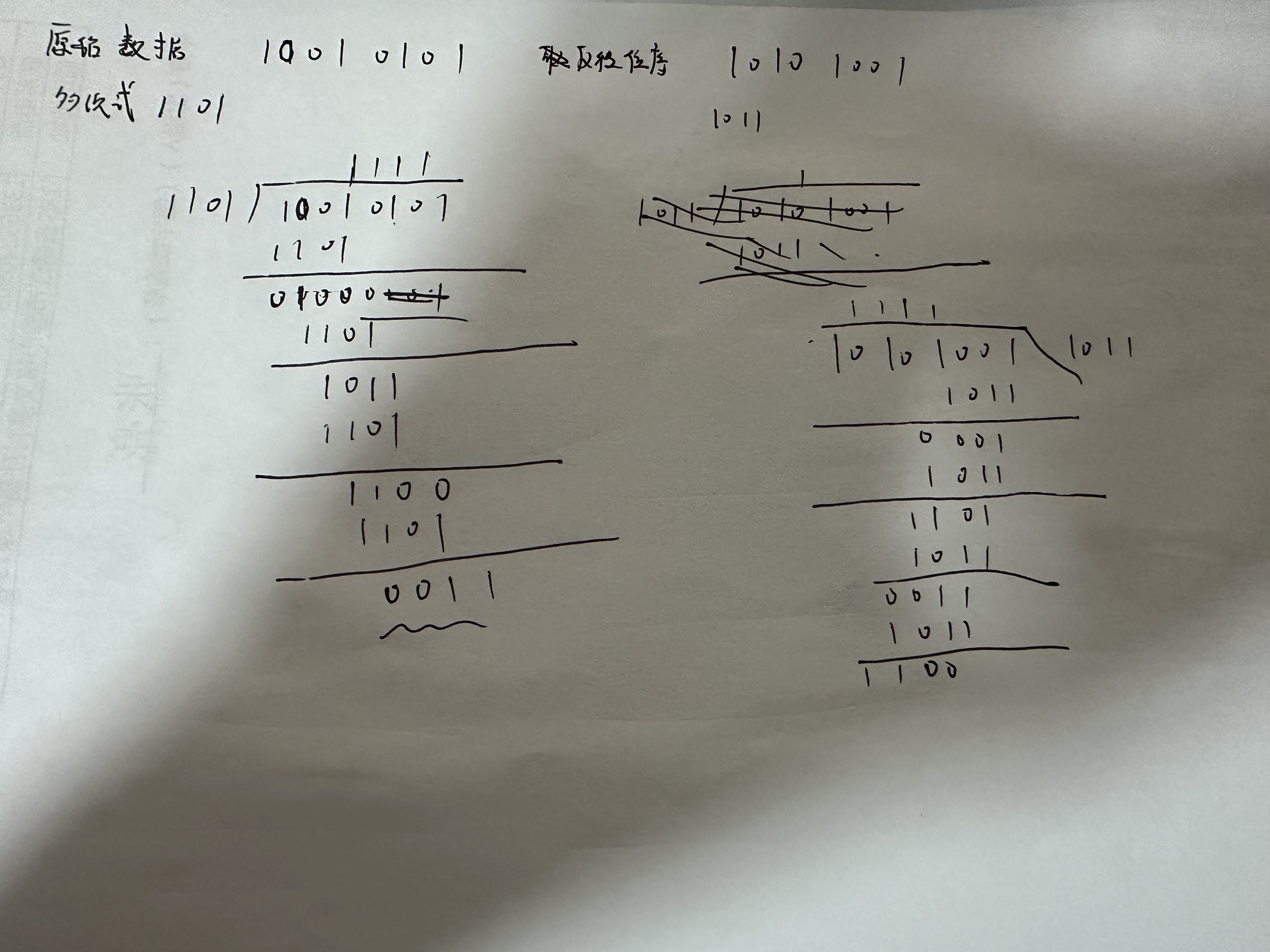当前位置：首页 > news >正文

关于Modbus CRC16生成算法的一些理解

news 2025/9/25 13:33:22

一、先贴一段计算的c++代码

二、代码中的计算方式以及与自行运算的相同和差异点

1、核心算法模2除法

2、CRC 基本介绍

3、结合代码

Init (初始值, Initial Value)

3.2 for循环（模2除法）

4、其中数学问题验证

三、其他易混淆的点

一、先贴一段计算的c++代码

传入参数可以自行调整

//  查表法
static uint16_t calculateCRC(const uint8_t* data, size_t length) {uint16_t crc = 0xFFFF;for (size_t i = 0; i < length; ++i) {uint8_t index = (crc ^ data[i]) & 0xFF;crc = (crc >> 8) ^ crcTable[index];}return crc;}//  单独计算法
static uint16_t calculateCRCManual(const std::vector<uint8_t>& data) {uint16_t crc = 0xFFFF;  // 固定初始值for (uint8_t byte : data) {crc ^= byte;  // 与当前字节异或for (int i = 0; i < 8; i++) {if (crc & 0x0001) {  // 检查最低位crc = (crc >> 1) ^ 0xA001;  // 固定多项式} else {crc >>= 1;}}}   return crc;
}// crc16的表 查表法要用
static const uint16_t crcTable[256] = {0x0000, 0xc0c1, 0xc181, 0x0140, 0xc301, 0x03c0, 0x0280, 0xc241,0xc601, 0x06c0, 0x0780, 0xc741, 0x0500, 0xc5c1, 0xc481, 0x0440,0xcc01, 0x0cc0, 0x0d80, 0xcd41, 0x0f00, 0xcfc1, 0xce81, 0x0e40,0x0a00, 0xcac1, 0xcb81, 0x0b40, 0xc901, 0x09c0, 0x0880, 0xc841,0xd801, 0x18c0, 0x1980, 0xd941, 0x1b00, 0xdbc1, 0xda81, 0x1a40,0x1e00, 0xdec1, 0xdf81, 0x1f40, 0xdd01, 0x1dc0, 0x1c80, 0xdc41,0x1400, 0xd4c1, 0xd581, 0x1540, 0xd701, 0x17c0, 0x1680, 0xd641,0xd201, 0x12c0, 0x1380, 0xd341, 0x1100, 0xd1c1, 0xd081, 0x1040,0xf001, 0x30c0, 0x3180, 0xf141, 0x3300, 0xf3c1, 0xf281, 0x3240,0x3600, 0xf6c1, 0xf781, 0x3740, 0xf501, 0x35c0, 0x3480, 0xf441,0x3c00, 0xfcc1, 0xfd81, 0x3d40, 0xff01, 0x3fc0, 0x3e80, 0xfe41,0xfa01, 0x3ac0, 0x3b80, 0xfb41, 0x3900, 0xf9c1, 0xf881, 0x3840,0x2800, 0xe8c1, 0xe981, 0x2940, 0xeb01, 0x2bc0, 0x2a80, 0xea41,0xee01, 0x2ec0, 0x2f80, 0xef41, 0x2d00, 0xedc1, 0xec81, 0x2c40,0xe401, 0x24c0, 0x2580, 0xe541, 0x2700, 0xe7c1, 0xe681, 0x2640,0x2200, 0xe2c1, 0xe381, 0x2340, 0xe101, 0x21c0, 0x2080, 0xe041,0xa001, 0x60c0, 0x6180, 0xa141, 0x6300, 0xa3c1, 0xa281, 0x6240,0x6600, 0xa6c1, 0xa781, 0x6740, 0xa501, 0x65c0, 0x6480, 0xa441,0x6c00, 0xacc1, 0xad81, 0x6d40, 0xaf01, 0x6fc0, 0x6e80, 0xae41,0xaa01, 0x6ac0, 0x6b80, 0xab41, 0x6900, 0xa9c1, 0xa881, 0x6840,0x7800, 0xb8c1, 0xb981, 0x7940, 0xbb01, 0x7bc0, 0x7a80, 0xba41,0xbe01, 0x7ec0, 0x7f80, 0xbf41, 0x7d00, 0xbdc1, 0xbc81, 0x7c40,0xb401, 0x74c0, 0x7580, 0xb541, 0x7700, 0xb7c1, 0xb681, 0x7640,0x7200, 0xb2c1, 0xb381, 0x7340, 0xb101, 0x71c0, 0x7080, 0xb041,0x5000, 0x90c1, 0x9181, 0x5140, 0x9301, 0x53c0, 0x5280, 0x9241,0x9601, 0x56c0, 0x5780, 0x9741, 0x5500, 0x95c1, 0x9481, 0x5440,0x9c01, 0x5cc0, 0x5d80, 0x9d41, 0x5f00, 0x9fc1, 0x9e81, 0x5e40,0x5a00, 0x9ac1, 0x9b81, 0x5b40, 0x9901, 0x59c0, 0x5880, 0x9841,0x8801, 0x48c0, 0x4980, 0x8941, 0x4b00, 0x8bc1, 0x8a81, 0x4a40,0x4e00, 0x8ec1, 0x8f81, 0x4f40, 0x8d01, 0x4dc0, 0x4c80, 0x8c41,0x4400, 0x84c1, 0x8581, 0x4540, 0x8701, 0x47c0, 0x4680, 0x8641,0x8201, 0x42c0, 0x4380, 0x8341, 0x4100, 0x81c1, 0x8081, 0x4040,};

上面这些不是本篇要说的重点

二、代码中的计算方式以及与自行运算的相同和差异点

1、核心算法模2除法

不做借位和进位，完全基于异或（XOR）操作；具体方法就不过多赘述，可以看一下模2除法——用非常直观的例子解释_模二除法-CSDN博客

需要注意一点就是末尾追加多少0 取决于多项式的长度一般为多项式长度减去1

2、CRC 基本介绍

CRC 的全称是循环冗余校验。它的本质是一种基于二进制除法的校验方法。

计算过程（发送方）：

将原始数据（比如 01 03 00 00 00 01）看作一个非常长的二进制数（比如可以看成 000000010000001100000000000000000000000000000001）。
在这个长二进制数的末尾追加若干个0（CRC-16就追加16个0）。这个新组成的数就是“被除数”。
用选定的生成多项式（Modbus协议默认0x18005）作为“除数”，对这个“被除数”进行一种特殊的模2除法（ XOR 运算，不进位也不借位）。
进行完这一系列除法操作后，最终得到的余数，就是 CRC 校验码。

3、结合代码

我们现在只看完整生成部分不看查表，仔细一点上来就可以发现第一个问题：

3.1 uint16_t crc = 0xFFFF; crc ^= byte; 为什么上来要和一个初始值0xFFFF 异或？

Init (初始值, Initial Value)

是什么：在开始CRC算法开始时寄存器（crc）的初始化预置值，十六进制表示。 Init 的位数和Poly（生成项）的位数相同，它的值为全0或者全F；
为什么需要：不同的协议标准要求不同的初始值。使用非零初始值（如0xFFFF）可以增加对前导0错误的检测能力，或者确保CRC计算对数据长度敏感。

先贴一下为什么与 0xFFFF异或：

根本性原理：非零初始值能最大程度地破坏计算的初始对称性，确保数据流中最早期的位错误也能被有效检测，从而全面提升CRC的雪崩效应和检错强度。
鲁棒性设计：为了统一且安全地处理所有可能的数据输入，包括那些理论上可能出现的边缘情况（如地址确实为0x00），保证校验算法在任何情况下都同样强大。
遵循成熟标准：继承自经过实战检验的CRC-16-IBM标准，这是一个在错误检测能力和实现效率上达到最佳平衡的、公认的优秀参数集。

扩展一下相关参数：

RefIn (输入反转, Input Reflection)：一个布尔值（True/False）。如果为True，则在处理每个字节之前，先将其位序反转。
RefOut (输出反转, Output Reflection)一个布尔值（True/False）。如果为True，则在整个CRC计算完成之后，但在进行最终异或操作之前，将整个CRC寄存器的位序进行反转。

需要注意的是 Refin 反转是每个字节每个字节反转字节之间的顺序没有变单个字节的位序变了如图1；Refout 是把一串数据从头到尾全反转即字节序也是反的如图2.

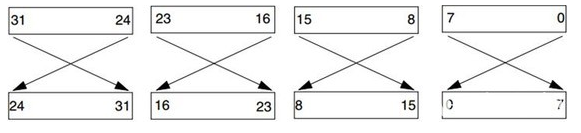
图1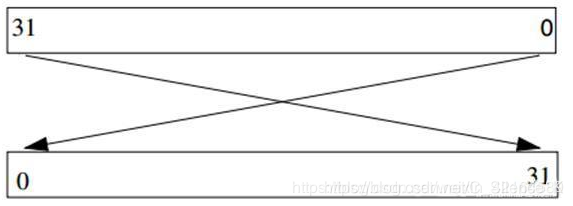

图2

如果想要看一步步推导出 crc码推荐看一下该文章CRC的计算过程你真的搞明白了吗？？_本原多项式的最大长度序列-CSDN博客

3.2 for循环（模2除法）

先解释一下这段循环代码是干什么的

① 首先检测了一下最低位是否为0；

② 若为0 右移高位自动补0；为1 与多项式0xA001异或

③ 依次循环八次（即一个字节位数）

在modbus协议中 默认设置RefIn 为true 即单个字节的位序反转（字节序正常），RefOut为true即把得到的crc值位序反转；此时的多项式为正序的0x18005,（最高位的1可以省略）；

循环这段代码等同于把一个字节位序反转然后与多项式做模二除法，第一次看可能觉得不直观非常抽象，举个例子：

正常crc运算流程
modbus 数据	01 06 00 01 00 2F
1.二进制展开在末尾添加2个字节的0	0000 0001 0000 0110 0000 0001 0000 0000 0010 1111 0000 0000 0000 0000
2.按字节位序反转	1000 0000 0110 0000 1000 0000 0000 0000 1111 0100 0000 0000 0000 0000
3.与初始值0xFFFF异或	1111 1111 1111 1111 0111 1111 1001 1111 1000 0000 0000 0000 1111 0100 0000 0000 0000 0000
4.与多项式0x8005模二运算	0111 1111 1001 1111 1000 0000 0000 0000 1111 0100 0000 0000 0000 0000 100 0000 0000 00101 0011 1111 1001 1101 0000 0000 0000 0000 1111 0100 0000 0000 0000 0000

代码中运算流程（单个字节一次运算）
modbus 数据	01 06 00 01 00 2F
1.二进制展开第一个数据 0x01与0xFFFF异或	0000 0000 0000 0001 1111 1111 1111 1111 1111 1111 1111 1110
2.与 0xA001 做模二运算不过他是从右往左	0000 1111 1111 1111 111 0 1 0100 0000 0000 001 1 1011 1111 1111 110 0

上面 01 数据进来后的变化用红色标注出来了，不难发现单个字节数据01进来后

按正常流程先位序反转在与初始值异或然后和正序多项式 0x8005做模二运算得到的结果与代码中不做位序反转先和初始值异或然后与反向多项式0xA001做模二运算后的结果是反序的；比如上面的是 0011 1111 下面的是 1111 1100 。

按照代码中得到的crc 值与正常运算得到的crc值是位序相反的；根据crc 标准 RefOut 决定了得到crc值后要进行位序反转；按照代码中的算法就刚好一步到位不需要在进行位序取反的操作了。

正常流程符合思维逻辑从左边往右边，代码中的方式则是从右往左，运算过程的每一步都是一样的，唯一不同点在于运算方向；下图就是随便写了一个例子，最后得到的余数位序相反

4、其中数学问题验证

上面的理解了之后问题来了：一个字节一个字节的进来并且进来后单个字节先和两个字节的crc寄存器进行异或然后经过八次运算（即一个字节长度）后加载另一个字节在进行以上运算，这样算出来的结果真的和正常运算得到的结果一样吗？

我们知道正常运算是把所有数据看作是一个长串数据进行的运算，而我们的处理方式是每个字节先和crc寄存器低八位异或然后做模二运算，得到的值与下个字节异或，所以我们现在要证明按字节序一个字节一个字节全部处理完后得到的结果和看作是整体处理的结果是一样的。

首先我们通过上面第3小节内容先明确一点代码中的方法处理一个字节数据和正常处理一个字节数据长度后结果只是位序相反，所以下面就以代码中的方向（从右往左）来表示运算流程的表格，先忽略掉与初始值的异或这样更直观。

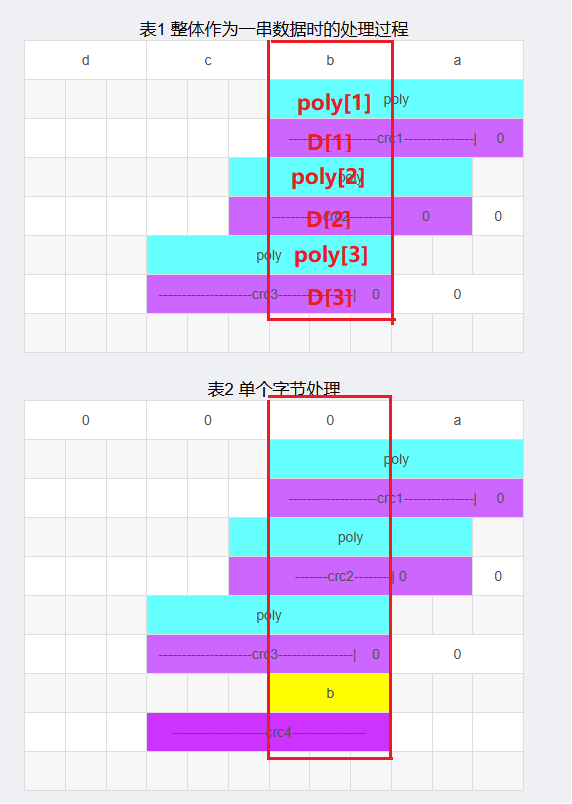
表1 整体作为一串数据时的处理过程
d c b a
poly
-------------------crc1---------------| 0
poly
-----------crc2---------| 0 0
poly
--------------------crc3----------------| 0 0

表2 单个字节处理
0 0 0 a
poly
-------------------crc1---------------| 0
poly
-------crc2--------| 0 0
poly
--------------------crc3----------------| 0 0
b
--------------------crc4----------------

蓝色：多项式紫色：当前crc值

观察上面的过程在下面的表中我们看到当数据a处理完后得到的crc将与b进行异或；现在只关注b字节数据对应在CRC寄存器中的值，就相当于画两条辅助线只观察CRC寄存器中这段数据，用字母D[i]来表示对应的这段数据；用字母poly[i]表示多项式中对应这段数据，如下图所示：

表1：

CRC1：D[1]= b ⊕ poly[1];

CRC2：D[2] = D[1] ⊕ poly[2];

CRC3：D[3] = D[2] ⊕ poly[3];

所以 D[3] = b ⊕ poly[1] ⊕ poly[2] ⊕ poly[3]

表2：

CRC1：D[1]= 0 ⊕ poly[1];

CRC2：D[2] = D[1] ⊕ poly[2];

CRC3：D[3] = D[2] ⊕ poly[3];

CRC4：D[4] = D[3] ⊕ b;

D[4] = 0 ⊕ poly[1] ⊕ poly[2] ⊕ poly[3] ⊕ b

根据异或的性质：①与 0 异或等于自身 ②异或的交换性

所以D[4] = b ⊕ poly[1] ⊕ poly[2] ⊕ poly[3]

上面两个表中的poly[i] 是对应的数据段是相等的；上面只是举例三次运算就移动了一个字节长度实际情况 i 是随机的8以内数字。同理当移动到数据c、d......等等时CRC寄存器中对应数据段是相等的，所以可以得出上下两种方式计算出的CRC值是相等的。

三、其他易混淆的点

就上面问题引申出另一个知识点：计算出CRC值后

1.位序反转

2. 把低字节数据放在前面高字节数据放后面。

位序反转是由于RefOut设定，高低字节交换顺序原因是什么呢？

CRC校验时是把接收到的数据与多项式进行模二除法，除完后余数应为0 ；

假设一串数据 01 03 00 01 00 02；

modbus默认设置 Init = 0xFFFF， RefIn = true；

0000 0001 0000 0011 0000 0000 0000 0001 0000 0000 0000 0010 0000 0000 0000 0000

1000 0000 1100 0000 0000 0000 1000 0000 0000 0000 0100 0000 0000 0000 0000 0000

1111 1111 1111 1111

0111 1111 0011 1111 0000 0000 1000 0000 0000 0000 0100 0000 0000 0000 0000 0000

100 0000 0000 0010 1

：

假设计算得到的CRC值为 0x563B 即 0101 0110 0011 1011

：

1000 0000 0000 0101

0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0101 0110 0011 1011

因为默认RefOut = true；位序反转：1101 1100 0110 1010 即0xDC6A

此时发送的数据是： 01 03 00 01 00 02 6A DC

接收方验证数据时按默认规则来字节位序反转

0000 0001 0000 0011 0000 0000 0000 0001 0000 0000 0000 0010 0110 1010 1101 1100

1000 0000 1100 0000 0000 0000 1000 0000 0000 0000 0100 0000 0101 0110 0011 1011

这个时候是不是对上了下面的黄色的对应上面红色的余数就相当于原始数据加上了余数所以模二运算验证结果就是0。

显而易见由于refout 所以crc值位序取反；这一操作其实相当于先把两个字节调换然后按字节位序取反，所以我们在得到最终crc值后把crc的低字节和高字节调换这样两个字节顺序又调换成正常顺序来，最后在接收方按字节位序取反得到的数据就是和余数一样了，模二除法算出结果与0作比较看是否传输过程中数据有误。

查看全文

http://www.dtcms.com/a/402991.html