前缀和算法:解锁高效编程的钥匙
1.【模板】一维前缀和
题目要求

题目分析:
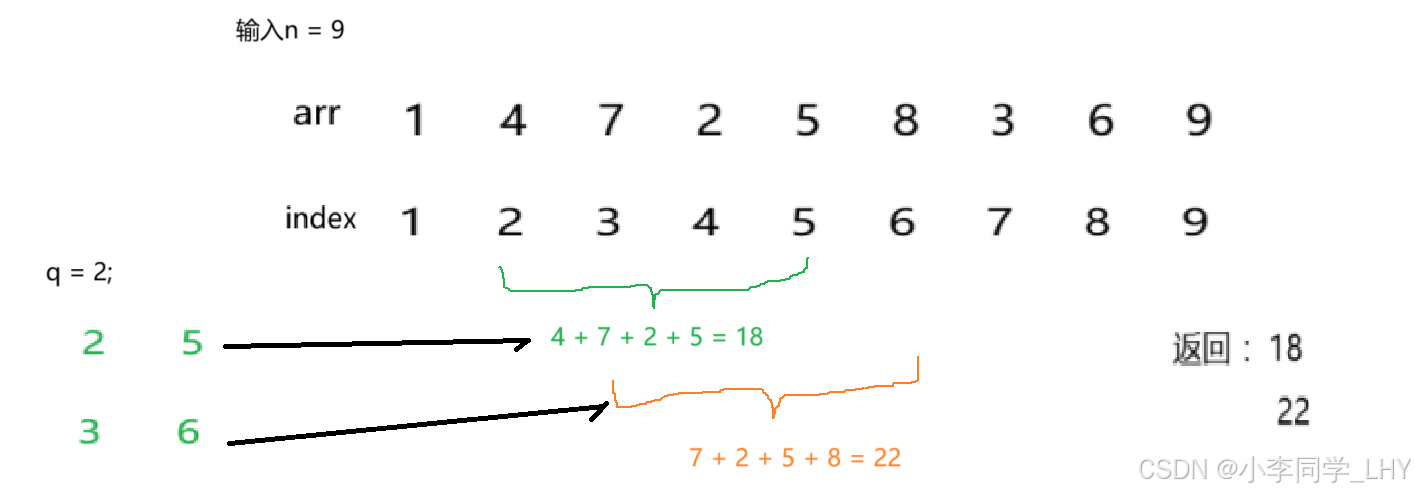
算法分析:
前缀和算法:快速求出数组中某一段连续区间的和。


代码步骤:
(1)输入数据
-
从标准输入读取两个整数
n和q:-
n表示数组的长度。 -
q表示查询的次数。
-
-
读取数组
arr,注意数组下标从1开始。
(2)前缀和数组
-
创建一个前缀和数组
prefix_sum,其中prefix_sum[i]表示数组arr中前i个元素的和。 -
前缀和的计算公式:
prefix_sum[i] = prefix_sum[i - 1] + arr[i];
(3)查询处理
-
对于每个查询,输入区间的左右边界
l和r。 - 使用前缀和数组快速计算区间和:
prefix_sum[r] - prefix_sum[l - 1]细节补充:设置前缀和数组时,定义第一个元素的下标为1,不是0,这样的目的是解决边界问题。
源代码:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//1.读入数据
int n = in.nextInt(),q = in.nextInt();
int[] arr = new int[n + 1];
for(int i = 1;i <= n; i++) arr[i] = in.nextInt();
//2.预处理一个前缀和数组
long[] prefix_sum = new long[n + 1];
for(int i = 1;i <= n;i++) prefix_sum[i] = prefix_sum[i - 1] + arr[i];
//3.使用前缀和数组
while(q > 0){
int l = in.nextInt(), r = in.nextInt();
System.out.println(prefix_sum[r] - prefix_sum[l - 1]);
q--;
}
}
}代码通过:

2.【模板】二维前缀和
题目要求:

题目解析:
 原理讲解:
原理讲解:



源代码:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//读入数据
int n = in.nextInt(),m = in.nextInt(),q = in.nextInt();
int[][] arr = new int[n + 1][m + 1];
for(int i = 1;i<=n;i++){
for(int j = 1; j<=m;j++){
arr[i][j] = in.nextInt();
}
}
//创建前缀和数组
long[][] dp = new long[n+1][m+1];
for(int i = 1;i<= n;i++){
for(int j = 1;j <= m ;j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];
}
}
//使用前缀和数组
while(q > 0){
int x1 = in.nextInt(),y1 = in.nextInt(),x2 = in.nextInt(),y2 = in.nextInt();
System.out.println(dp[x2][y2] -dp[x1-1][y2] -dp[x2][y1-1] + dp[x1-1][y1-1]);
q--;
}
}
}代码解析:
(1)输入数据
-
从标准输入读取三个整数
n、m和q:-
n表示二维数组的行数。 -
m表示二维数组的列数。 -
q表示查询的次数。
-
-
读取二维数组
arr,注意数组下标从1开始。
(2)二维前缀和数组
-
创建一个二维前缀和数组
dp,其中dp[i][j]表示从arr[1][1]到arr[i][j]的子矩阵的和。 -
前缀和的计算公式:
dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];
(3)查询处理
-
对于每个查询,输入子矩阵的左上角
(x1, y1)和右下角(x2, y2)。 -
使用前缀和数组快速计算子矩阵和:
dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]
代码通过:

3. 寻找数组的中心下标
题目描述:
算法原理:

根据题目要求,如果要求当前下标 i,则
- 左边要判断的是0 ~ i-1 元素的和
- 右边要判断的是n-1 ~ i+1元素的和
使用前缀和思想
预处理两个数组,分别存放i下标左边和右边元素之和。
注意:不要加上i下标的元素(别跟前面的前缀和题搞混)
第一步:
f 数组存放前缀和 :

g数组存放后缀和:
第二步:
注意细节:
- f(0)表示nums[ 0 ]位置左边默认为0(因为没有元素),同时处理边界问题,g[ n - 1 ]亦如此。
- g数组存放后缀和,存放顺序记得从右向左,为了和f数组找对应下标

第三步:
只需用循环同时遍历f数组和g数组即可如果f[ i ] == g[ i ] ,那就是该下标
举例:

源码:
class Solution {
public int pivotIndex(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
//预处理两个数组
for(int i = 1; i < n ; i++){
f[i] = f[i - 1] + nums[ i - 1];
}
for(int i = n -2; i >= 0 ; i--){
g[i] = g[i + 1] + nums[ i + 1];
}
//找到下标
for(int i = 0 ; i < n ;i++){
if(f[i] == g[i]) return i;
}
return -1;
}
}给定一个整数数组 nums,找到一个下标 i,使得:
-
下标
i左边的元素之和等于右边的元素之和。 -
如果不存在这样的下标,返回
-1。
-
预处理两个数组:
-
f[i]:表示下标i左边元素的和(不包括nums[i])。 -
g[i]:表示下标i右边元素的和(不包括nums[i])。
-
-
计算
f和g:-
f[i] = f[i - 1] + nums[i - 1]:从左到右累加。 -
g[i] = g[i + 1] + nums[i + 1]:从右到左累加。
-
-
寻找中心下标:
-
遍历数组,找到满足
f[i] == g[i]的下标i。 -
如果找不到,返回
-1。
-

4. 除自身以外数组的乘积
算法原理:
和上一道题类似,也是除了本身元素,计算左边和右边的积
第一步:


第二步:
注意细节:
f [ 0 ] 此时要变成 1,不然相乘全为0,g[n - 1] 同理;
第三步:
新创一个数组,遍历存放即可;
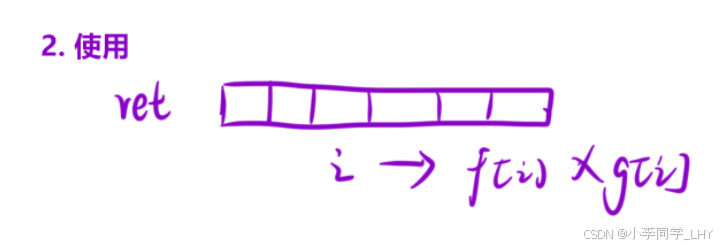 比如:
比如:

源码:
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
f[0] = 1;
for(int i = 1;i<n;i++){
f[i] = f[i - 1] * nums[i - 1];
}
g[n-1] = 1;
for(int i = n-2 ;i>=0;i--){
g[i] = g[i + 1] * nums[i + 1];
}
int[] ret = new int[n];
for(int i = 0;i<n;i++){
ret[i] = f[i] * g[i];
}
return ret;
}
}-
第一次遍历(使用数组
f)计算从左到右的累积乘积。f[i]存储的是nums[0]到nums[i-1]的乘积(注意f[0]被初始化为1,因为没有元素在nums[0]的左边)。 -
第二次遍历(使用数组
g)计算从右到左的累积乘积。g[i]存储的是nums[i+1]到nums[n-1]的乘积(注意g[n-1]被初始化为1,因为没有元素在nums[n-1]的右边)。 -
最后,通过遍历数组
nums,用f[i]和g[i]的乘积来填充结果数组ret,这样ret[i]就包含了除了nums[i]以外的所有元素的乘积。

5.和为 K 的子数组
题目要求:
 算法原理:前缀和 + 哈希表(记住一段区间元素之和,其实等于前缀和的一个数字)
算法原理:前缀和 + 哈希表(记住一段区间元素之和,其实等于前缀和的一个数字)
第一步:

第二步:
使用哈希表存放前缀和出现的次数。

第三步:

源代码:
class Solution {
public int subarraySum(int[] nums, int k) {
// 哈希表,记录前缀和及其出现次数
Map<Integer, Integer> hash = new HashMap<>();
hash.put(0, 1); // 前缀和为 0 的情况出现了 1 次
int sum = 0; // 当前前缀和
int ret = 0; // 结果:满足条件的子数组个数
for (int x : nums) {
sum += x; // 计算当前前缀和
// 如果存在前缀和 sum - k,则说明从某个位置到当前位置的子数组和为 k
ret += hash.getOrDefault(sum - k, 0);
// 更新当前前缀和的出现次数
hash.put(sum, hash.getOrDefault(sum, 0) + 1);
}
return ret; // 返回结果
}
}
6.和可被 K 整除的子数组
题目要求:
算法原理:前缀和 + 哈希表
前提引入两个结论:
1.同余定理:如果(a - b) % k = 0 ,则a % k == b % k;(记住结论,不证明)
举例:(26 - 12 ) % 7 = 0,所以 26 % 7 = 12 % 7 = 5;
2. 修正余数:
- 负数 % 正数 = 负数;比如(a 是 负数 ,b是正数)
- a % b (负数)
- a % b + b (变为正数,但是a和b都是正数,则余数会错)
- (a % b + b) % b(最终令正负统一)
第一步:

第二步:
使用哈希表存放前缀和的余数与出现的次数。

第三步:细节与上一题类似
源代码:
class Solution {
public int subarraysDivByK(int[] nums, int k) {
// 哈希表,记录前缀和对 k 取模的结果及其出现次数
Map<Integer, Integer> has = new HashMap<>();
has.put(0 % k, 1); // 前缀和对 k 取模为 0 的情况出现了 1 次
int sum = 0; // 当前前缀和
int ret = 0; // 结果:满足条件的子数组个数
for (int x : nums) {
sum += x; // 计算当前前缀和
// 计算当前前缀和对 k 取模的结果,并处理负数情况
int r = (sum % k + k) % k;
// 如果存在前缀和对 k 取模的结果 r,则说明从某个位置到当前位置的子数组和能被 k 整除
ret += has.getOrDefault(r, 0);
// 更新当前前缀和对 k 取模的结果 r 的出现次数
has.put(r, has.getOrDefault(r, 0) + 1);
}
return ret; // 返回结果
}
}
7.连续数组
题目要求:

算法原理:前缀和 + 哈希表(哈希表存放的是前缀和 和 对应的下标)
第一步:

第二步:
 源代码:
源代码:
class Solution {
public int findMaxLength(int[] nums) {
// 哈希表,记录前缀和及其第一次出现的位置
Map<Integer, Integer> hash = new HashMap<>();
hash.put(0, -1); // 前缀和为 0 的情况出现在索引 -1
int sum = 0; // 当前前缀和
int ret = 0; // 结果:最长满足条件的子数组长度
for (int i = 0; i < nums.length; i++) {
// 将 0 视为 -1,1 视为 1
sum += (nums[i] == 0 ? -1 : 1);
// 如果哈希表中存在当前前缀和 sum,则更新结果
if (hash.containsKey(sum)) {
ret = Math.max(ret, i - hash.get(sum));
} else {
// 否则,将当前前缀和 sum 及其索引 i 存入哈希表
hash.put(sum, i);
}
}
return ret; // 返回结果
}
}


