小杰机器学习(seven)——贝叶斯分类
1. 贝叶斯分类理论讲解
1.1 贝叶斯原理
贝叶斯算法是基于贝叶斯公式的,其公式为:
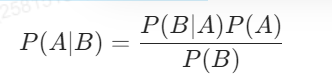

1. 先验概率(Prior Probability)
先验概率是指在观察到任何数据或证据之前,我们对某件事情发生的初始信念或概率估计。它是根据以往的经验、知识或者假设来确定的。先验概率反映了我们对未知参数或假设的先验知识。
2.似然概率是什么?
似然概率(likelihood)是一个统计学概念,通常用于描述给定模型参数的情况下观测数据出现的可能性。似然是概率论中的一个重要概念,但它与概率有所不同。似然通常用来衡量某个假设(比如参数取值)与实际观测数据之间的一致性程度。
3.后验概率(Posterior Probability)
后验概率是指在获得新的证据或数据后,我们更新的概率估计。它是根据先验概率以及新的观测数据,通过应用贝叶斯定理得到的结果。
4.极大似然估计和贝叶斯估计有什么不同?
极大似然估计(MLE, Maximum Likelihood Estimation):通过最大化数据在某一假设模型下的似然函数来估计模型参数。它只依赖数据,不考虑参数的先验信息。 贝叶斯估计(Bayesian Estimation):结合先验分布和数据,通过贝叶斯公式来更新对参数的信念。贝叶斯估计既考虑了数据的似然函数,也结合了参数的先验知识,因此具有更灵活的解释性。 区别在于:极大似然估计仅考虑观测数据,而贝叶斯估计通过引入先验分布,能够融入之前的知识进行推断。
贝叶斯引入-例子:
假如你约异性出来看电影,异性可能会同意,也可能不同意,这由TA对你的态度决定。
如果TA喜欢你,你约TA出来的成功率为100%,
如果是无所谓的话,约TA出来的成功率为30%,约了几次之后,
你想知道TA对你的态度是什么,
那么就可以根据贝叶斯公式来计算出TA对你持哪种态度的可能性更高。
贝叶斯的作用:根据已知的概率来更新事件的概率。(喜欢你的概率)
例子的概念:
先验概率:假设有一个先验信念关于TA对你的态度——这里假设有50%的概率TA喜欢你,50%的概率TA对你无所谓。
似然概率:你约TA看电影,TA的反应(接受或者拒绝)是似然概率。如果TA喜欢你(A事件),TA接受邀请(B事件)的概率是100%。如果TA对你无所谓(非A事件),TA接受的概率是30%。
使用贝叶斯公式更新:可以使用TA对你的邀请做出的反应来更新关于TA对你的感觉。
例如:你发出来邀请,TA接受了邀请,你可以用贝叶斯定理来更新TA喜欢你的概率。
A事件:TA喜欢你
B事件:接受邀请
求P(TA喜欢你|接受邀请)的概率?
P(A|B)=[P(A)*P(B|A)]/P(B)
例子带入公式中:
A事件是TA喜欢你,B事件是接受邀请。
P(A|B)是在TA接受邀请后,TA喜欢你的后验概率;
P(B|A)是TA喜欢你时接受邀请的概率,即100%
P(A)是TA喜欢你的先验概率(假设一个人对另一个人喜欢不喜欢的概率都是50%)
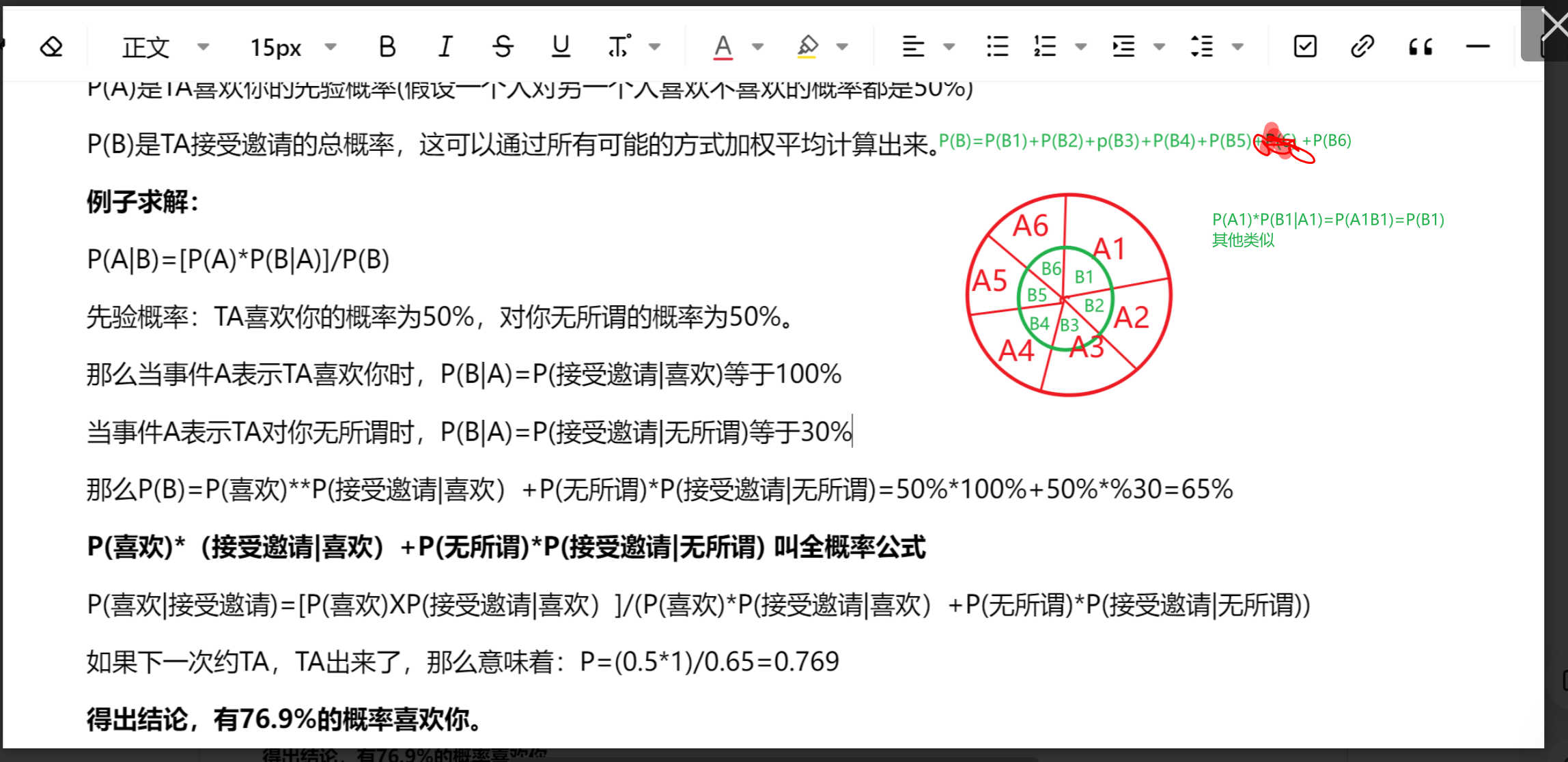
P(B)是TA接受邀请的总概率,这可以通过所有可能的方式加权平均计算出来
例子求解:
P(A|B)=[P(A)*P(B|A)]/P(B)
先验概率:TA喜欢你的概率为50%,对你无所谓的概率为50%。
那么当事件A表示TA喜欢你时,P(B|A)=P(接受邀请|喜欢)等于100%
当事件A表示TA对你无所谓时,P(B|A)=P(接受邀请|无所谓)等于30%
那么P(B)=P(喜欢)*P(接受邀请|喜欢)+P(无所谓)*P(接受邀请|无所谓)=50%*100%+50%*%30=65%
P(喜欢)*(接受邀请|喜欢)+P(无所谓)*P(接受邀请|无所谓) 叫全概率公式
P(喜欢|接受邀请)=[P(喜欢)*P(接受邀请|喜欢)]/((P(喜欢)*P(接受邀请|喜欢)+P(无所谓)*P(接受邀请|无所谓))
如果约一次TA出来了,那么意味着:P=(0.5*1)/0.65=0.769
得出结论,有76.9%的概率喜欢你。
全概率公式解释
贝叶斯垃圾邮件分类
假设邮箱里有50封邮件:
红色代表垃圾邮件共10封,蓝色代表非垃圾邮件共40封。
P(垃圾邮件)=10/50=0.2
P(非垃圾邮件)=40/50=0.8

邮件正文中可能有“彩票”这个词
其中:垃圾邮件有“彩票”这个词的有7封。
P(包含彩票|垃圾邮件)=7/10=0.7
非垃圾邮件有“彩票”这个词的有5封
P(包含彩票|非垃圾邮件)=5/40=0.125

贝叶斯垃圾邮件分类
P(垃圾邮件)=10/50=0.2 P(非垃圾邮件)=40/50=0.8
P(包含彩票|垃圾邮件)=7/10=0.7 P(包含彩票|非垃圾邮件)=5/40=0.125
计算:如果一封邮件中包含“彩票”,垃圾邮件的概率是多少?
把贝叶斯公式拿过来
P(A|B)=[P(A)XP(B|A)]/P(B)
A事件是垃圾邮件
B事件是包含彩票这个词的事件
P(垃圾邮件|包含彩票)=[P(垃圾邮件)XP(包含彩票|垃圾邮件)]/[P(包含彩票|垃圾邮件)*P(垃圾邮件)+P(包含彩票|非垃圾邮件)* P(非垃圾邮件)]
P(垃圾邮件|包含彩票)=(0.2x0.7)/(0.2x0.7+0.8*0.125)=0.583
贝叶斯的先验与后验
贝叶斯可以通过一个模板把整个过程进行提炼
先验P(A) | 事件(Event) | 后验 |
垃圾邮件分类中 P(A)=P(垃圾邮件) =垃圾邮件数量/总数量 =0.2 | 垃圾邮件分类中 Event=包含“彩票” | 垃圾邮件中 P(A|E) 代表:有“彩票”2字垃圾邮件的可能性 |
约会大作战中 P(A)=P(喜欢) =喜欢或者无所谓 =0.5 | 约会大作战中 Event=同意出去玩 | 约会大作战中 P(A|E) 代表:同意出去玩喜欢你的概率 |
朴素贝叶斯
定义:
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。
为啥要引入朴素贝叶斯?
事件是包含“彩票”与“中奖”怎么办?
先验P(A) | 事件(Event) | 后验 |
垃圾邮件分类中 P(A)=P(垃圾邮件) =垃圾邮件数量/总数量 =0.2 | 垃圾邮件分类中 Event=包含“彩票” | 垃圾邮件中 P(A|E) 代表:有“彩票”2字垃圾邮件的可能性 |
垃圾邮件分类中 P(A)=P(垃圾邮件) =垃圾邮件数量/总数量 =0.2 | 垃圾邮件分类中 Event=包含“彩票”和“中奖” | ? |
事件包含“彩票”与“中奖”计算时的问题
事件 | 后验 |
垃圾邮件分类中 Event=包含“彩票”与“中奖” | P(垃圾邮件|"彩票 "与“中奖”) |
贝叶斯公式:
P(A|B)=[P(A)*P(B|A)]/P(B)
P(垃圾邮件|“彩票”与“中奖”)=[P(垃圾邮件)XP(“彩票”与“中奖”|垃圾邮件)]/[P(“彩票”与“中奖”|垃圾邮件)*P(垃圾邮件)+P(“彩票”与“中奖”|非垃圾邮件)* P(非垃圾邮件)]
P(“彩票”与“中奖”|垃圾邮件)概率怎么算?
P(“彩票”与“中奖”|垃圾邮件)=(包含彩票与中奖的垃圾邮件数量/垃圾邮件数量)
事件是包含100个垃圾词的情况
事件 | 后验 |
垃圾邮件分类中 Event=包含100个垃圾词 | P(垃圾邮件|100个垃圾词) |
P(垃圾邮件|100个垃圾词)=[P(垃圾邮件)XP(词1...词100|垃圾邮件)]/[P(词1...词100|垃圾邮件)*P(垃圾邮件)+P(“词1...词100|非垃圾邮件)* P(非垃圾邮件)]
不会同时出现100个垃圾词的邮件,就算有的概率也非常低,在更多垃圾词的情况下,分子会变成0 后验就求不出来了。
随着事件的变得更复杂的情况下,就会导致没办法直接通过贝叶斯求解你的概率。
那怎么解决事件复杂的情况下概率求解的问题?
现在拿只有“彩票”和“中奖”这个案例来说如何解决?
P(垃圾邮件|“彩票”与“中奖”)=[P(垃圾邮件)XP(“彩票”与“中奖”|垃圾邮件)]/[P(“彩票”与“中奖”|垃圾邮件)*P(垃圾邮件)+P(“彩票”与“中奖”|非垃圾邮件)* P(非垃圾邮件)]
对于P(“彩票”与“中奖”|垃圾邮件)概率的求解不直接计算,进行估算概率。
估算概率使用一个方案叫朴素假设
朴素假设的是:在邮件中,“彩票”和“中奖”两个词的出现时相互独立的。
其实在机器学习和深度学习中会把很多事件给它假设为独立性事件。
朴素贝叶斯的“朴素”之处在于它假设特征之间相互独立,即给定类别,一个特征的出现不影响其他特征的出现。这在现实世界中通常不成立,但在许多情况下,这种简化的假设仍然能够提供良好的分类性能。
实际上这种情况是不正确的,和真实的完整的数学解是不一样的,是有问题的,比如在自然语言处理中,“早上好”,现在是把“早上”和“好”认为是独立的,实际是有关系的。所以朴素假设是估算,基本上是没有问题的,大差不差。比它大就是比它大,比它小就是比它小,是相对值的概念。
如果把彩票和中奖当作独立性事件。
P(垃圾邮件|“彩票”与“中奖”)
=[P(垃圾邮件)*P(“彩票”|垃圾邮件)*P(“中奖”|垃圾邮件)]/[P(“彩票”|垃圾邮件)*P(“中奖”|垃圾邮件)*P(垃圾邮件)+P(“彩票”|非垃圾邮件)*P(“中奖”|非垃圾邮件)* P(非垃圾邮件)]
朴素贝叶斯求解
50封邮件,垃圾邮件10封 非垃圾邮件40封

带彩票的邮件中
P(垃圾邮件)=10/50=0.2
P(非垃圾邮件)=40/50=0.8
P(包含彩票|垃圾邮件)=7/10=0.7
P(包含彩票|非垃圾邮件)=5/40=0.125

带中奖的邮件中
P(垃圾邮件)=10/50=0.2
P(非垃圾邮件)=40/50=0.8
P(包含中奖|垃圾邮件)=8/10=0.8
P(包含中奖|非垃圾邮件)=4/40=0.1

列出来:
带彩票的邮件中 带中奖的邮件中
P(垃圾邮件)=10/50=0.2 P(垃圾邮件)=10/50=0.2
P(非垃圾邮件)=40/50=0.8 P(非垃圾邮件)=40/50=0.8
P(包含彩票|垃圾邮件)=7/10=0.7 P(包含中奖|垃圾邮件)=8/10=0.8
P(包含彩票|非垃圾邮件)=5/40=0.125 P(包含中奖|非垃圾邮件)=4/40=0.1
P(垃圾邮件|“彩票”与“中奖”)
=[P(垃圾邮件)*P(“彩票”|垃圾邮件)*P(“中奖”|垃圾邮件)]/[P(“彩票”|垃圾邮件)*P(“中奖”|垃圾邮件)*P(垃圾邮件)+P(“彩票”|非垃圾邮件)*P(“中奖”|非垃圾邮件)* P(非垃圾邮件)]
=(0.2X0.7X0.8)/(0.2X0.7X0.8+0.8X0.125X0.1)=0.918
如果邮件中包含中奖和彩票垃圾邮件的概率是91.8%
贝叶斯为什么能做分类任务?
贝叶斯分类器能够进行分类任务,主要基于贝叶斯定理,其步骤如下:先计算先验概率,即数据集中各类别出现概率,反映无额外信息时样本属于某类的概率;再算条件概率,即给定类别下观察到特定特征的概率。接着应用贝叶斯定理,由先验和条件概率算出后验概率,即观察到特征后样本属于某类的概率。最后,分类器选后验概率最高的类别作为预测结果。朴素贝叶斯假设特征独立,简化算法且效果良好。
1.2 准备数据
在本实验中,准备了两类散点,其分布如下图所示:
蓝色点的坐标分别为:[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]。
红色点的坐标分别为:[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]。
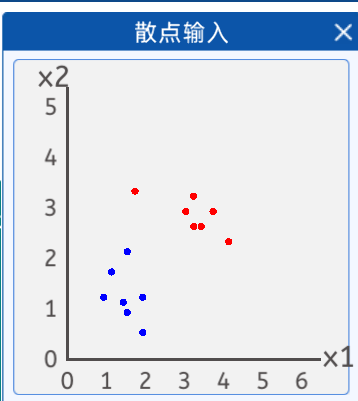
图上有“红色点”和“蓝色点”根据两类点绘制出分类边界,然后判断二维坐标系的其他点属于哪一类。
贝叶斯判断我们的某个点是在蓝色的区域还是在红色的区域。比如把蓝色点设置为0 ,把红色点设置为1。就可以在0.5位置绘制决策边界,所以说可以使用贝叶斯来实现一个分类的。
那怎么使用贝叶斯来实现上面蓝色点和红色点的分类呢?
贝叶斯的公式如下:
P(A|B)=[P(A)XP(B|A)]/P(B)
在贝叶斯中 有先验 事件(Event) - > 后验
在当前实例中,先看一下先验
从图上可以观察到有两类点,蓝色点和红色点。
先验:A事件,当前某类点的类别。
事件:B事件,是当前点的特征向量(当前例子是坐标(X1,X2))
P(A)就是当前某类点(蓝色点或者红色点)占的比例。
P(B|A)指的是知道类别的情况下,点的坐标是多少。
P(B|A)怎么计算呢?
它不能直接通过某个东西计算,需要去估计或者假设(比如它属于红色点的时候 坐标概率是什么,属于蓝色点的时候,坐标概率是什么?)。
坐标是不是连续数据,这里估计或者假设的函数可以用高斯分布的概率密度函数来估计,之所以这样做,是因为在很多自然条件下,随机变量分布都会趋向于高斯分布,因此高斯分布经常被用作连续变量分布中作为概率分布的假设。
高斯分布在实际应用中非常重要,因为许多自然界和社会现象都可以近似地用高斯分布来描述,特别是当样本量较大时。在机器学习和深度学习中,高斯分布被广泛用于建模和估计参数,尤其在概率模型和最大似然估计中有着重要的应用。在当前实例中P(B|A)=高斯概率密度函数
P(B) 是观测到的给定数据的一个概率,假设每一个点都是存在的,P(B)在当前例子中就是观测到红色点或者蓝色点的概率。在当前例子中数据点不属于红色就属于蓝色,全概率公式计算后的P(B)=1。
后验概率=先验概率*高斯分布概率密度函数=P(A)XP(B|A)
1.3 计算先验概率
先验概率的计算很简单,就是将当前类别的点(红色数据点和蓝色数据点),比如当事件A表示红色点时,先验概率![]() 就是红色点的个数/所有点的个数,也就是7/14=0.5。事件A表示蓝色点时,计算过程一样。
就是红色点的个数/所有点的个数,也就是7/14=0.5。事件A表示蓝色点时,计算过程一样。
1.4 条件概率计算
条件概率计算=计算高斯分布概率密度函数
对于当前例子,有两个变量 x1 和x2,使用多元高斯分布概率密度函数。




在概率论和统计学中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。其定义的数学形式是:
![]()

公式中n指的是样本的数量
协方差矩阵的代码
#协方差矩阵使用numpy实现
import numpy as np
#假设计算协方差矩阵的数据为 3个样本 5个特征
X=np.array([[0,2],[1,1],[2,0]])
#numpy自带np.cov()
# np.cov(m,rowvar)
#m: 可以是一维或者二维数组,m的每一行代表一个变量,每一列包含所有随机变量的一个观测值#当给一维数组时,相当于计算方差
#rowvar指定了行、列哪一维表示随机变量的问题,默认为True,即行代表一个随机变量,而列代表观测值# 如果为False,那么列代表随机变量,而行代表观测值。
print(f"输入是 行代表一个随机变量,而列代表观测值\n",np.cov(X))
print(f"输入是 列代表一个随机变量,而行代表观测值\n",np.cov(X,rowvar=False))1.5 计算后验概率
有了先验概率和概率密度函数后,就可以求解后验概率了。

1.6坐标点的分类
坐标点绘制效果如下
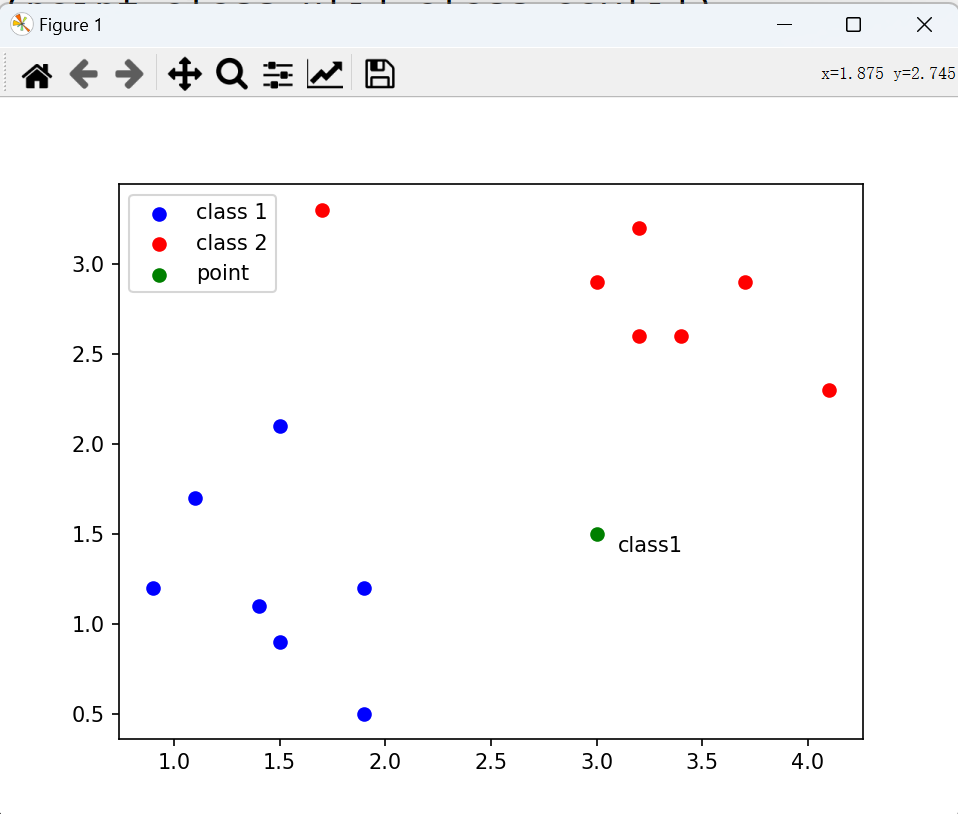
代码实现
import numpy as np
import matplotlib.pyplot as plt
# 1.散点输入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
#合并数据集 创造标签
X=np.concatenate((class1_points,class2_points),axis=0)
Y=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class1_points))),axis=0)
#计算一下先验概率
prior_prob=[np.sum(Y==0)/len(Y),np.sum(Y==1)/len(Y)]
# print(prior_prob)
#计算条件概率 多元高斯分布的概率密度函数
#计算蓝色点和红色的均值
class_μ=[np.mean(X[Y==0],axis=0),np.mean(X[Y==1],axis=0)]
# print(class_μ)
#求协方差矩阵
class_cov=[np.cov(X[Y==0],rowvar=False),np.cov(X[Y==1],rowvar=False)]def pdf(x,mean,cov):# 1.获取均值向量的长度,即特征的数量n=len(mean)#计算系数# numpy.linalg.det()函数计算输入矩阵的行列式coff=1/((2*np.pi)**(n/2)*np.sqrt(np.linalg.det(cov)))#计算指数部分# np.dot()计算两个一维数组的内积#np.linalg.inv 求逆exponent=np.exp(-(1/2)*np.dot(np.dot((x-mean).T,np.linalg.inv(cov)),(x-mean)))return coff*exponentpoint=np.array([3.2,3.5])
#存储后验结果
poster_prob=[]
for i in range(2):# 使用概率密度函数求条件概率likelihood=pdf(point,class_μ[i],class_cov[i])# 计算后验概率=先验*条件概率poster_prob.append(prior_prob[i] * likelihood)
pre_class=np.argmax(poster_prob)
#绘制散点图
plt.scatter(class1_points[:,0],class1_points[:,1],c="blue",label="class 1")
plt.scatter(class2_points[:,0],class2_points[:,1],c="red",label="class 2")
plt.scatter(point[0],point[1],c="green",label='point')
#添加图例
plt.legend()
#将预测点的标签属于哪类标注出来
if pre_class==0:plt.text(point[0]+0.1,point[1]-0.1,s="class1")
else:plt.text(point[0] + 0.1, point[1] - 0.1, s="class2")
plt.show()
决策边界的代码演示
import numpy as np
import matplotlib.pyplot as plt# 1.散点输入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])#合并数据集 创造标签
X=np.concatenate((class1_points,class2_points),axis=0)
Y=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class1_points))),axis=0)
print(Y)
# 2.计算先验
# 2.1 每一个类别的数据在数据集中的比例
prior_prob=[np.sum(Y==0)/len(Y),np.sum(Y==1)/len(Y)]#3.计算高斯分布的概率密度函数
# 求解包括蓝色点数据的均值 和红色点数据的均值
class_μ=[np.mean(X[Y==0],axis=0),np.mean(X[Y==1],axis=0)]
#求协方差矩阵
class_cov=[np.cov(X[Y==0],rowvar=False),np.cov(X[Y==1],rowvar=False)]
#使用for循环进行求解高斯概率密度函数
#获取新的坐标点(x1,x2)def pdf(x,mean,cov):#1.获取均值向量的长度,即特征的数量n=len(mean)#2计算系数# numpy.linalg.det()函数计算输入矩阵的行列式coff=1/((2*np.pi)**(n/2)*np.sqrt(np.linalg.det(cov)))#3计算指数部分# np.dot()计算两个一维数组的内积exponent=np.exp(-(1/2)*np.dot(np.dot((x-mean).T,np.linalg.inv(cov)),(x-mean)))return coff*exponent#获得xy轴上的足够多的坐标点 ,用于从坐标向量构造网格
xx,yy=np.meshgrid(np.arange(0,5,0.05),np.arange(0,4,0.05))
#拿到预测点
# np.c_沿着矩阵的第二个轴拼接
grid_points=np.c_[xx.ravel(),yy.ravel()]# point=np.array([3,1.5])
#存储后验结果
grid_label=[]
#预测网格点
for point in grid_points:poster_prob = []for i in range(2):#使用概率密度函数求条件概率likelihood=pdf(point,class_μ[i],class_cov[i])#计算后验概率=先验*条件概率poster_prob.append(prior_prob[i]*likelihood)pre_class=np.argmax(poster_prob)grid_label.append(pre_class)
#绘制散点图
plt.scatter(class1_points[:,0],class1_points[:,1],c="blue",label="class 1")
plt.scatter(class2_points[:,0],class2_points[:,1],c="red",label="class 2")
# plt.scatter(point[0],point[1],c="green",label='point')
#添加图例
plt.legend()
#显示决策边界
#预测标签和xx形状一致
#列表先转成数组
grid_label=np.array(grid_label)
pre_grid_label=grid_label.reshape(xx.shape)
#等高线绘制
contour=plt.contour(xx,yy,pre_grid_label,level=0.5,color='green')plt.show()2. 贝叶斯多分类理论讲解
贝叶斯多分类也用的贝叶斯公式:
与贝叶斯分类的不同之处在于贝叶斯多分类的类别较多,前面贝叶斯分类是两分类现在大于两分类
2.1 准备数据
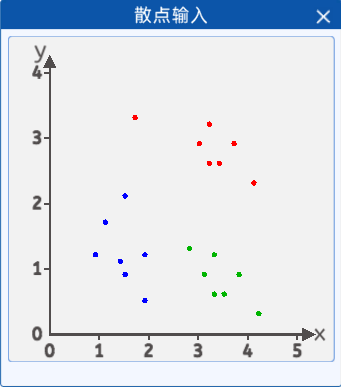
三类散点,分别为“喜欢你”、“无所谓”、“讨厌你”,这里准备了共21个点作为数据,将其抽象成散点分布在二维坐标中,其分布如下图所示:
蓝色点的坐标分别为:[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]。
红色点的坐标分别为:[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]。
绿色点的坐标分别为:[3.3, 1.2],[3.8, 0.9],[3.3, 0.6],[2.8, 1.3],[3.5, 0.6],[4.2, 0.3],[3.1, 0.9]。
2.2 计算先验概率
“红色点”的先验概率就是“红色点”的个数除以总个数;“蓝色点”的先验概率就是“蓝色点”的个数除以总个数;“绿色点”的先验概率就是“绿色点”的个数除以邮件的总个数。对应到散点图中,就是各类点的个数除以点的总个数。

2.3 条件概率计算
条件概率计算=计算高斯分布概率密度函数
对于当前例子,有两个变量 x1 和x2,使用多元高斯分布概率密度函数。
下面讲解一下多元高斯分布

高斯分布联合概率密度公式:
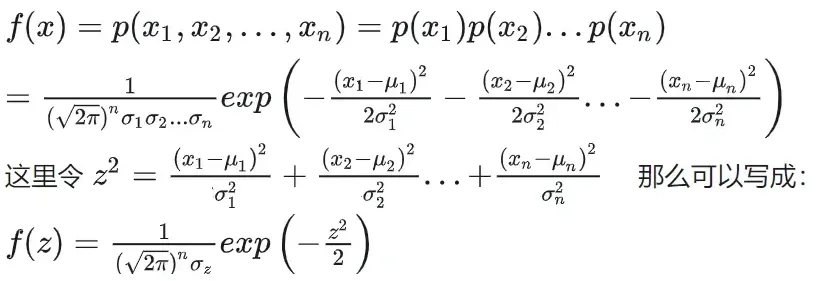
不妨从几何的思想角度来考虑问题,将![]() 转换为矩阵乘积形式:
转换为矩阵乘积形式:

这里假设的是x的维度之间是相互独立的,因此对角线以外的地方协方差为0(不相关),对角线的协方差就是方差。
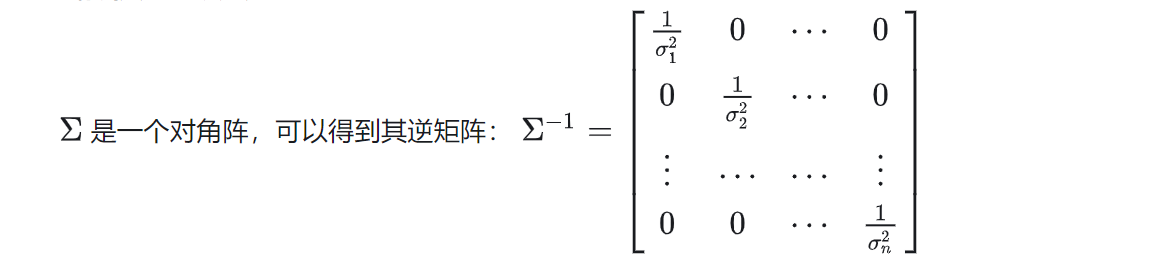
根据性质对角阵的行列式就是对角元素的乘积可知:
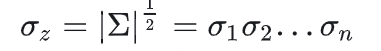
![]()
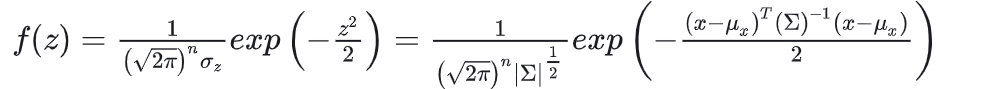
化简整理一下得多元高斯分布的概率密度函数:

在概率论和统计学中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。其定义的数学形式是:
![]()

公式中n指的是样本的数量
将每一类的对应数据带入该公式中,即可求得对应每一类的概率密度值。
多分类代码演示
import numpy as np
import matplotlib.pyplot as plt# 1.散点输入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])class3_points = np.array([[3.3, 1.2],[3.8, 0.9],[3.3, 0.6],[2.8, 1.3],[3.5, 0.6],[4.2, 0.3],[3.1, 0.9]])#合并数据集 创造标签
X=np.concatenate((class1_points,class2_points,class3_points),axis=0)
Y=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class1_points)),np.ones(len(class1_points))+1),axis=0)
print(Y)
# 2.计算先验
# 2.1 每一个类别的数据在数据集中的比例
prior_prob=[np.sum(Y==0)/len(Y),np.sum(Y==1)/len(Y),np.sum(Y==2)/len(Y)]#3.计算高斯分布的概率密度函数
# 求解包括蓝色点数据的均值 和红色点数据的均值
class_μ=[np.mean(X[Y==0],axis=0),np.mean(X[Y==1],axis=0),np.mean(X[Y==2],axis=0)]
#求协方差矩阵
class_cov=[np.cov(X[Y==0],rowvar=False),np.cov(X[Y==1],rowvar=False),np.cov(X[Y==2],rowvar=False)]
#使用for循环进行求解高斯概率密度函数
#获取新的坐标点(x1,x2)def pdf(x,mean,cov):#1.获取均值向量的长度,即特征的数量n=len(mean)#2计算系数# numpy.linalg.det()函数计算输入矩阵的行列式coff=1/((2*np.pi)**(n/2)*np.sqrt(np.linalg.det(cov)))#3计算指数部分# np.dot()计算两个一维数组的内积exponent=np.exp(-(1/2)*np.dot(np.dot((x-mean).T,np.linalg.inv(cov)),(x-mean)))return coff*exponent#获得xy轴上的足够多的坐标点
xx,yy=np.meshgrid(np.arange(0,5,0.05),np.arange(0,4,0.05))
#拿到预测点
# np.c_沿着矩阵的第二个轴拼接
grid_points=np.c_[xx.ravel(),yy.ravel()]# point=np.array([3,1.5])
#存储后验结果
grid_label=[]
#预测网格点
for point in grid_points:poster_prob = []for i in range(3):#使用概率密度函数求条件概率likelihood=pdf(point,class_μ[i],class_cov[i])#计算后验概率=先验*条件概率poster_prob.append(prior_prob[i]*likelihood)pre_class=np.argmax(poster_prob)grid_label.append(pre_class)
#绘制散点图
plt.scatter(class1_points[:,0],class1_points[:,1],c="blue",label="class 1")
plt.scatter(class2_points[:,0],class2_points[:,1],c="red",label="class 2")
plt.scatter(class3_points[:,0],class3_points[:,1],c="yellow",label="class 3")
# plt.scatter(point[0],point[1],c="green",label='point')
#添加图例
plt.legend()
#显示决策边界
#预测标签和xx形状一致
#列表先转成数组
grid_label=np.array(grid_label)
pre_grid_label=grid_label.reshape(xx.shape)
#等高线绘制
contour=plt.contour(xx,yy,pre_grid_label,colors='black')plt.show()