Deep Residual Learning for Image Recognition 阅读笔记

Title

标题：
Deep Residual Learning for Image Recognition
用于图像识别的深度残差学习
发布：EEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016

作者：
Kaiming He 何恺明
简介：
2003-2007年就读于清华大学物理系基础科学班，连续3年获得清华奖学金，本科毕业后进入香港中文大学攻读研究生，师从汤晓鸥。2009年成为CVPR最佳论文首位华人得主。2011年获得香港中文大学信息工程哲学博士学位，之后进入微软亚洲研究院工作。

Abstract

背景：
越深的神经网络越难训练
方法：
提出了残差（residual）学习框架
结果：
评估了深度高达152层的残差网络-比VGG网络深8倍，但仍然具有较低的复杂性
结论：
在 ImageNet检测、ImageNet定位、COCO检测和 COCO分割任务中获得了第一名。

Results

本文章没有写，内容篇幅太大，CVPR 限制页数

Introduction

• 第一段：介绍了卷积神经网络非常重要：在ImageNet数据集上取得了领先的结果

• 第二段：提出疑问：学习更好的网络是否像堆叠更多层那样简单?障碍是梯度消失/爆炸，这个问题已经通过normalized initialization和intermediate normalization layers得到了很大程度的解决，这些技术使得数十层的网络能够 通过反向传播的随机梯度下降(SGD)开始收敛。

• 第三段：暴露出另一个问题：随着网络深度的增加，准确率会趋于饱和，然后迅速下降
  如图：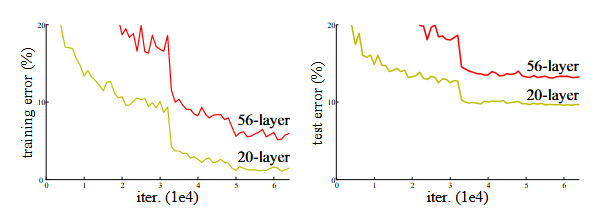

• 第四段：这种退化难以优化：对于更深模型存在一个构造性解:新增层为恒等映射,其他层则复制自已学习的较浅模型，这种构造解的存在意味着更深模型产生的训练误差不应高于其较浅对应物。

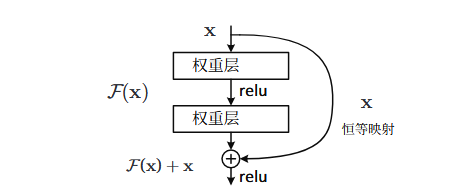
• 第五段：提出的方法：深度残差框架（deep residual learning framework），将期望的基础映射表示为 H(x),我们让堆叠的非线性层拟合另一个映射 F (x):= H(x) −x，基础映射被重写为H(x)=F(x)+x。
  

• 第六段：捷径连接：跳过一层或多层的连接，捷径连接执行恒等映射，其输出与堆叠的输出相加F(x)+x，但是既不增加参数也不增加复杂度

• 第七段：优点：1)我们的极深度残差网络易于优化,而对应的“普通”网络(仅简 单堆叠层)在深度增加时表现出更高的训练误差;2) 我们的深度残差网络能够轻松从大幅增加的深度中获得准确率提升,产生显著优于先前网络的结果。

• 第八段：普适性：不止适用于特定的数据集，还探索了1000层的模型

• 第九段：模型对比：深度VGG深，复杂度比VGG低，错误率比VGG低。

Related Work

• 残差表示：对于向量 量化,编码残差向量已被证明比编码原始向量更有效。
• 捷径连接：练多层感知器(MLPs)的早期实践是添 加一个从网络输入连接到输出的线性层。

Deep Residual Learning

3.1 Residual Learning

• 第一段：介绍残差学习：让我们将 H(x)视为由若干堆叠层拟合的基础映射,其中x 表示这些层中第一层 的输入。假设多个非线性层可以渐进逼近复杂函数,那么这等价于假设它们可以渐进逼近残差函数, 即,H(x) − x。不需要逼近H(x)，而是逼近残差函数F(x)=H(x)-x，所以H(x)=F(x)+x
• 第二段：退化问题表明：求解器难以通过叠加层来逼近恒等映射，但是通过残差学习，如何恒等映射是最优解，就可以通过叠加层来逼近恒等映射
• 第三段：现实情况：恒等映射大概率不是最优解，但是我们的方法也有助于寻找扰动。

3.2 Identity Mapping by Shortcuts

• 第一段：继续定义残差框架：H(x)=F(x)+x，
• 第二段：捷径连接优点：既未增加参数，也没有增加复杂度
• 第三段：恒等映射足以解决退化问题且更为经济
• 第四段：残差函数更加灵活，一般包含两三层，如果是单层就像一个线性层
• 第五段：这种方法不仅可以简化全连接层还可以简化卷积层

3.3 Network Architectures

普通网络结构与残差网络结构的对比
普通网络结构

• 卷积层采用3×3 filters
• 相同输出feature map ，filters数量相同
• 若feature map size减半，filters数量加倍
• 采用步长（stride）为2的卷积层下采样
• 网络末端采用全局平均池化层和带softmax的1000路全连接
• 图中加权层34层
  残差网络结构
• 在普通网络结构的基础上，加上了捷径连接（shortcut connections）
• 输入维度与输出维度相同时，可以使用捷径连接
• 当维度增加时（1）使用捷径连接，通过补0的方式增加维度，不增加参数（2）通过1×1的卷积匹配维度

3.4 Implementation

• 权重初始化
• 开始训练残差网络
• 使用批量大小256×256的梯度下降
• 学习率0.1
• 60 × 10 4次方 iterations（迭代）
• weight decay（权重衰减） of 0.0001
• momentum（动量） of 0.9

Experiments

4.1. ImageNet Classification

介绍了一下两种模型在数据集中的结果

• 数据集包含1000个分类
• 在128w张图片上训练 用5w张图片作为验证集评估
• 在10万张测试图像 上的最终结果。我们同时评估了top-1和top-5错误率。

普通网络

• 34层网络比18层网络更深，却有更高的验证误差，细线表示训练误差,粗线表示中心裁剪的验证误差
  
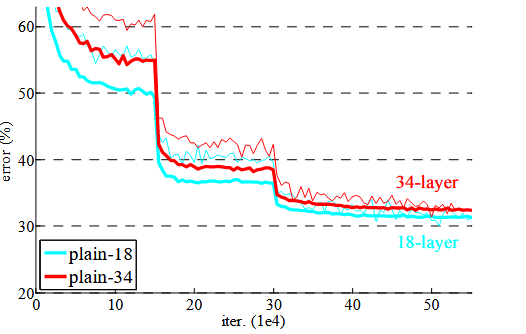
• 这种优化困难不太可能是由梯度消失引 起的。

残差网络

• 18层和34层残差网络 。基线架构与上述普通网络相同
• 在每对 3×3 滤波器间添加了快捷连接（shortcut connections）
• 我们对所有快捷连接使用恒等映射（identity mapping）,并通过零填充增加维度，并没有增加复杂度
• 34层残差网络优于18层残差网络提升2.8%
• 34层残差网络展现 出显著更低的训练误差,并能泛化至验证数据
• 有效解决了退化问题，残差学习在极深系统中极具有效性。
• 当网络“不过深”(此处为18层)时,当前随机梯 度下降求解器仍能为普通网络找到良好解。

恒等映射 vs. 投影捷径

提出了三种方案
(A) 使用零填充捷径进行维度提升,且所有捷径均为无参数
(B) 使用投影捷径进行维度提升, 其他捷径为恒等映射
© 所有捷径均为投影

结果：
所有三个选项都明显优于普通网络。 B略优于A。我们认为这是因为A中的零填充维度实际上没有残差学习。C比B稍好

更深的瓶颈架构

• 对于残差函数使用三层堆叠而不是两层
• 分别为1×1、3×3、和 1×1 卷积，其中 1×1 层负责减少然后增加(恢复)维度,使 3×3 层成为具有较小输入/输出维度的瓶颈。
• 
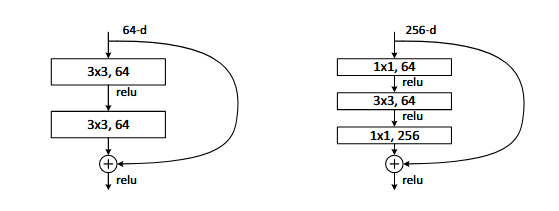
  ResNet50：将34层网络中的每个2层块替换为 3层瓶颈块,从而得到一个50层ResNet，
  ResNet101/152：层数增加了，但是复杂度仍然低于VGG-16/19，层数的增加确实没有导致模型退化

4.2. CIFAR-10与分析

数据集介绍：5万张训练图像和1万张测试图像，10个类别

• 输入32×32图像
• 第一层3×3卷积
• 随后使用一系列 6n 层,分别在尺寸为 {32, 16, 8} 的特征图上进行 3×3 卷积
• 每种特征图尺 寸对应 2n 层
• 滤波器数量分别为 {16, 32, 64}
• 子采样通过步长为2的卷积实现
• 网络以全局平均池化、 10路全连接层和softmax作为结尾。