【C++】二叉搜索树 和 AVL树——思想
目录
🌟一、二叉搜索树
🌟二、AVL树(平衡二叉树)
🌟三、AVL树插入节点的四种情况
🌟四、单起目录 -> 目录3的剩余两种情况
🌟五、旋转总结
🌟六、AVL树删除节点
🌟七、完结

🌟一、二叉搜索树
时间复杂度
二叉搜索树,可提供对数时间的元素插入和访问。它在搜索,插入,删除时的平均时间复杂度是O(log n),它在创建时的平均时间复杂度是O(n log n),因为要创建n次。
注意我说的都是平均,也就是说并不都是平均的情况,之后我们会讲解。
二叉搜索树的节点放置规则
在二叉搜索树中,任何一个节点的键值一定大于它的左子树的每一个键值,并小于它的右子树的每一个键值。
简单来说就是,左子树的键值比这个键值小,右子树的键值比这个键值大。
因此二叉搜索树找最小值或者最大值非常容易找到,只要一直向左走或者向右走就可以找到,一直向左走就可以找到最小值,一直向右走就可以找到最大值。
二叉搜索树比较麻烦的是插入节点和删除节点。
插入新节点
插入新节点时,从根节点开始,遇到比插入节点较大的节点就向左走,遇到比插入节点小的节点就向右走。
这里文字描述实在是不清晰,看接下来的图吧
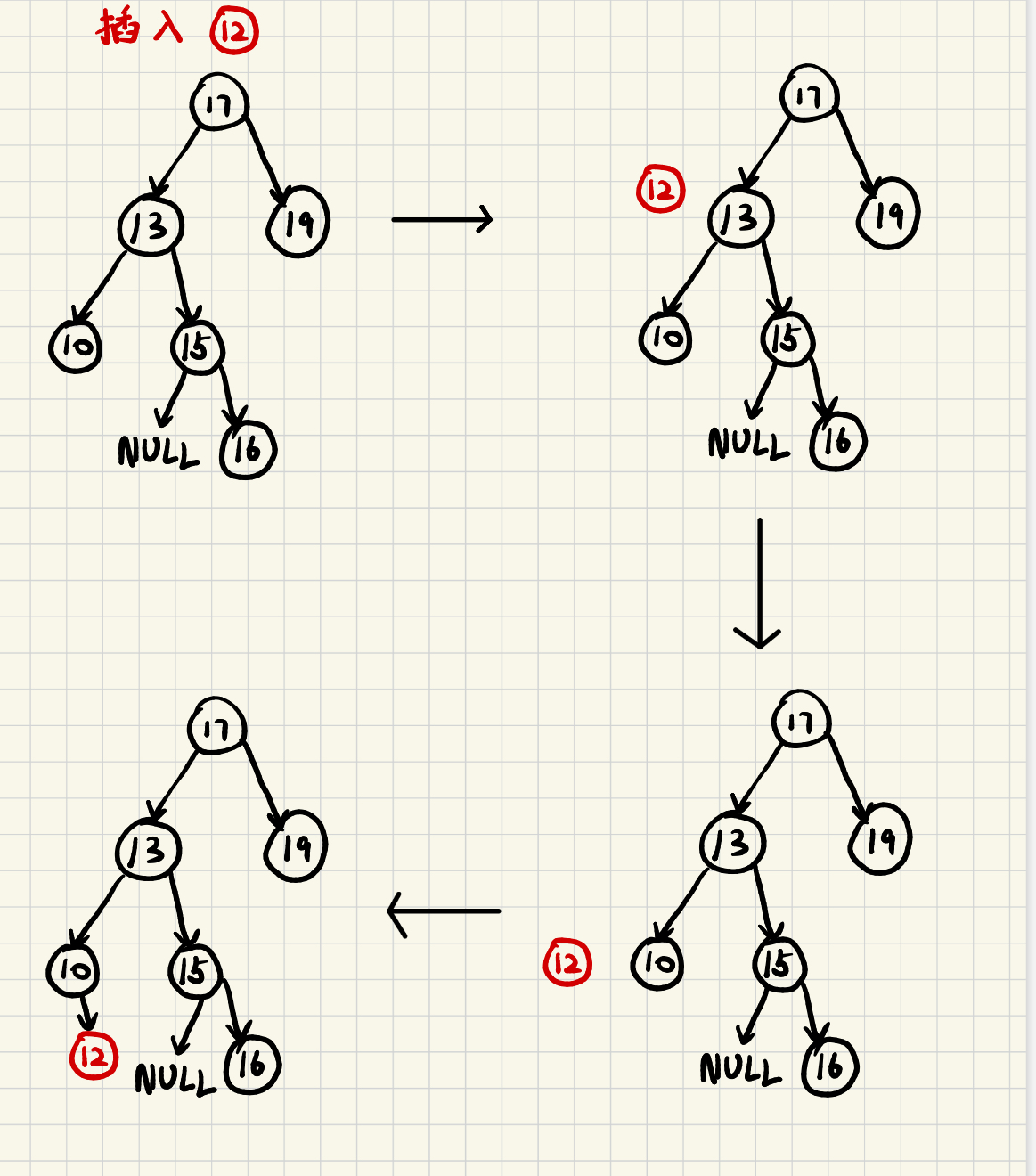
不需要思考为什么插入的是12,不放在13的左边,再把10放在12的左边。我们的二叉搜索树的主要目的是为了加快查找所需键值时的时间复杂度,因此不必强制有序。
移除旧节点
在移除二叉搜索树的旧节点时。如果它是叶节点,直接拿走即可。
如果它有一个节点,那就把这个节点补上去。
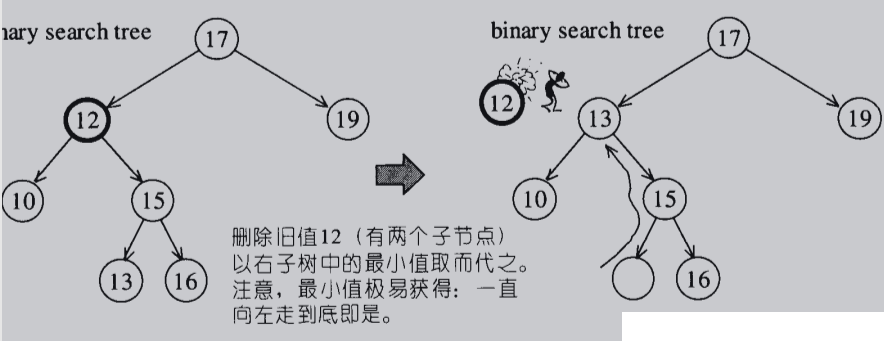
如果它有两个节点,那就把它右节点的最小的后代节点补上去。如图 ->:
🌟二、AVL树(平衡二叉树)
时间复杂度
AVL树又称作平衡二叉树,它在搜索,插入,删除时的时间复杂度是O(log n)。它在创建时的时间复杂度是O(n log n),因为要创建n次
平衡二叉树的引入
平衡二叉树的出现是为了弥补二叉搜索树的效率问题。我们在二叉搜索树开头处,提到了时间复杂度,但是我说的都是" 平均 "情况,那就有不是平均的情况。如下图->:
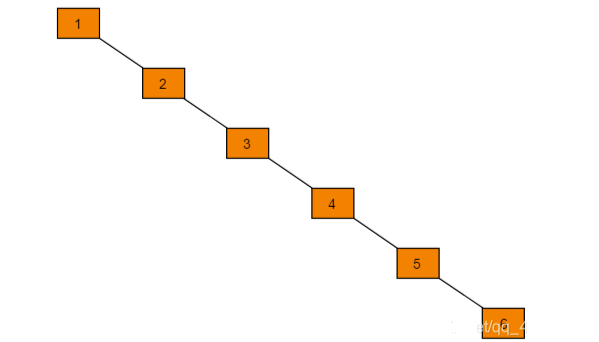
如果我们插入的是{1,2,3,4,5,6},那么时间复杂度就不是对数了,而是一个 O(n) 了,为了解决这种问题,引入了平衡二叉树的存在
从本质上来看,AVL树是对二叉搜索树的一种优化。
哪里优化了?
因为二叉搜索树的效率取决于树的高度,因此,只要保持树的高度最小,那么二叉搜索树的效率就会得到提高,而AVL树就是为了解决这种问题。如下图 -> :
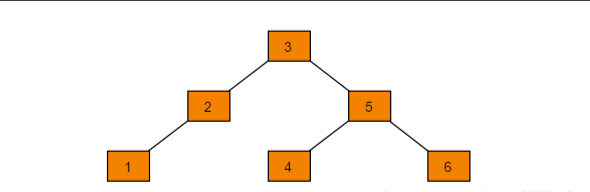
同样是插入{1,2,3,4,5,6}, 因为树的高度减小了,所以查找的效率变快了。如果我们要查找6,直接从二叉搜索树的6次,优化到了现在的3倍,可见提高效率之高。
当节点数目一定,保持树的左右两端保持平衡,树的查找效率最高。
这种左右子树的高度相差不超过1的树为平衡二叉树。
平衡因子
在AVL树中,我们用 " 平衡因子 "来判断原本的二叉搜索树需不需要优化,也就是说让二叉搜索树构成AVL树。
某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子(BF,Balance Factor)
平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。如果某一结点的平衡因子绝对值大于1则说明此树不是平衡二叉树
高度height
在二叉搜索树中,我们新增了一个变量值 height ,每一个节点都有一个只属于自己的height变量,这个变量用于记录每个节点的高度,通过每个节点的高度,计算出它当前所对应的平衡因子
如果平衡因子的绝对值超过了1,那就说明当前节点的平衡因子不是-1,0,1了,需要修改为平衡二叉树
🌟三、AVL树插入节点的四种情况
插入节点
平衡二叉树的构成,在于每个节点的height,如果想要构成平衡二叉树,需要我们检查从新插入节点到根节点这条路径上,所有祖先节点的平衡因子。因为我们新插入一个节点,只会改变它们的平衡因子。
因为平衡因子的定义,一个节点的左子树与右子树的高度差,因此新节点的插入影响的只有从它插入进来的这条路径的所有祖先节点的平衡因子。
插入节点破坏平衡性有如下四种情况
平衡二叉树之所以能实现,是因为及时止损。也就是说,当出现平衡因子不对劲的时候,就立刻修改。不是等全插入完了后再一起修改,那样会非常的混乱。
往平衡二叉树中添加节点可能会导致二叉树失去平衡,所以我们需要在每次插入节点后进行平衡的维护操作。插入节点破坏平衡性有如下四种情况:
LL (右旋)
这里先解释什么叫LL,这里只解释一遍,往后讲的都是同理。 第一个字母代表的是树,第二个字母代表的是孩子,LL 所代表的就是 -> 向此节点的 左子树(L) 插入 左孩子(L)导致的AVL树失衡,叫做LL
那右旋是什么意思 ?我们接下来讲右旋,但需要知道的是,LL不是右旋的意思,是说,当出现LL的时候,我们需要进行右旋这个操作。
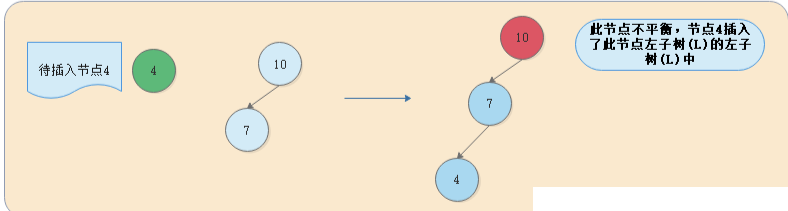
如图->:当我们插入新的节点4时,因为4要插在7的左边,这就导致了节点10的平衡因子失衡。
那么对于10这个节点来说,这就是在往我的左子树插入左孩子导致的失衡,属于LL,因此我要进行右旋了 !
小插曲 ->: 为什么能知道是10这个节点失衡了? 因为我们刚才说过,我们插入一个节点要检查它到根结点这段"插入路径"的所有它的祖先节点,当检查出来不平衡时,就及时更改,及时止损
右旋操作 -> : 把当前节点放在它的左孩子节点的右子树上
可以这么记,就是绕着孩子向右顺时针旋转,既然是向右旋转了,那必然是左孩子,因为指向左孩子的指针恰好可以向右顺时针旋转
如下图 -> :
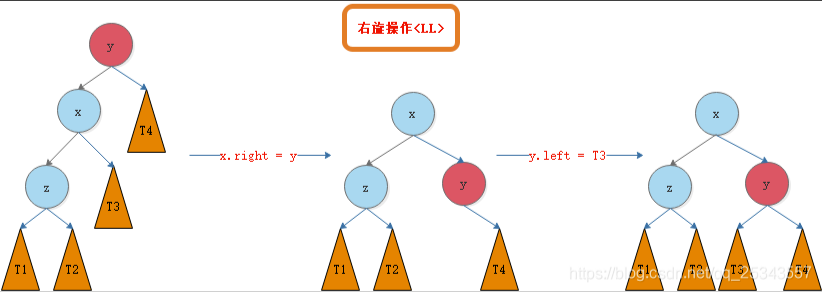
如果把当前节点放在它的孩子节点的右子树上时,发现孩子节点的右节点怎么办?
如图所示,把孩子节点的右节点放在父节点的左边去就好了,因为要进行右旋的节点,(LL)它右旋后左节点一定是空的。这里不懂得可以思考一下
右旋后要记得更新每个节点的平衡因子
图解过程->:
RR (左旋)
RR就是往当前节点的右子树(R)插入右节点(R),如图所示->:
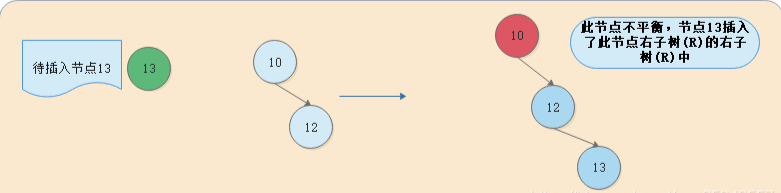
对此,我们需要进行左旋
左旋
左旋操作就是把当前节点放在它右孩子节点的左边,如下图 ->:
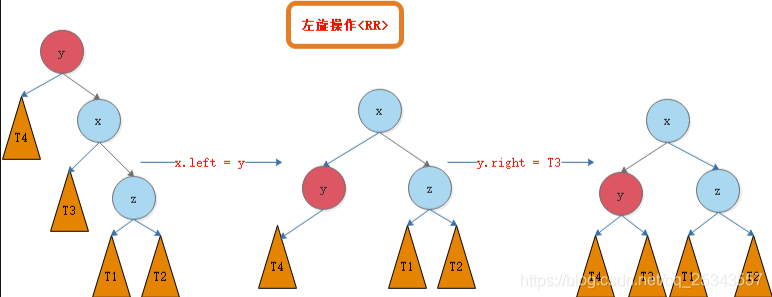
如果它孩子节点的左边有节点,就把孩子节点的左节点变成当前节点的右节点。其实这种操作不需要特殊背。因为父节点一定会空出来一条指针,这条指针必须承接被 "遗落" 的节点
图解过程->:
🌟四、单起目录 -> 目录3的剩余两种情况
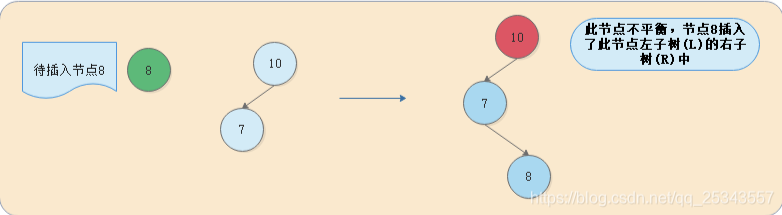
LR
LR,就是往当前节点的左子树(L)插入右节点(R)导致的平衡因子失衡,如下图->:
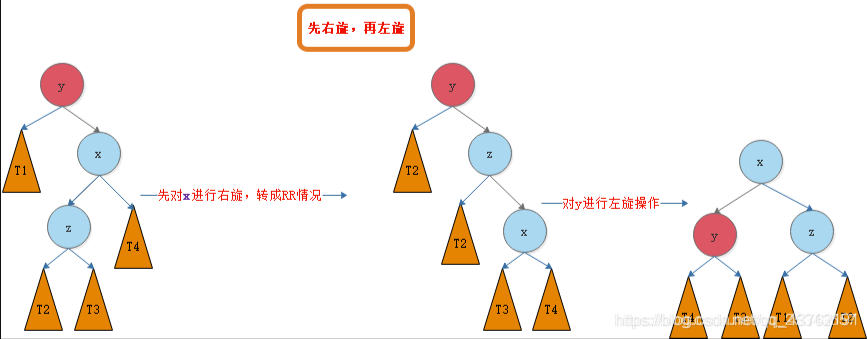
对于 LR ,我们需要先将其变成 LL,再对其进行右旋。
先将其变成LL,是先将当前节点的左孩子节点进行左旋变成LL
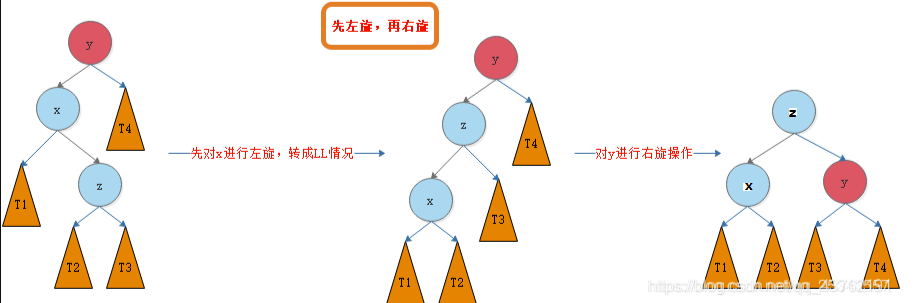
RL
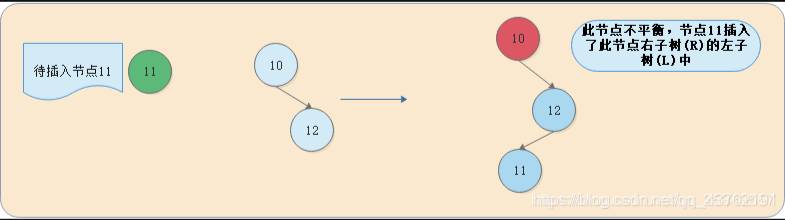
RL就是对当前节点的右子树(R)插入左孩子(L)
对于这种情况,我们先变成RR形态,变成RR形态就要对当前节点的右孩子节点进行右旋变成RR
🌟五、旋转总结
相信讲了这么多旋转还是有点绕的,这里总结一下
1. LL (右旋)
2. RR(左旋)
3. LR(先变成LL,再进行右旋)(LR型 -> 让当前节点的左孩子进行左旋 -> LL型)
4. RL(先变成RR,再进行左旋)(RL型 -> 让当前节点的右孩子进行右旋 -> RR型)
特别需要注意的是,无论是LL,还是RR,RL,LR型,这些类型并不只有在插入节点时才存在,当我们在删除节点时,依然可以发现组成LL,RR,RL,LR型形状的节点,在删除节点时依旧使用。
🌟六、AVL树删除节点
在AVL树删除节点后,是有可能破坏平衡因子的,因此在AVL树中删除节点,我们需要计算其平衡因子,以免不再是AVL树
我们删除节点后,需要判断哪些节点的平衡因子呢?我们思考一下,我们在插入加点时,影响的是我们插入节点这条路径的所有祖先节点的平衡因子。
那我们删除节点时,从被删除节点的位置开始,沿着父节点一路向上回溯,直到根节点。这条路径上的每一个节点都需要检查平衡因子并进行修复。
为什么要向上检查 ? 不向下检查 ?
当你删除节点时,删除节点之前,每个节点都是处于平衡状态的。而你删除一个节点,是需要被删除节点的下面的节点来顶替你的。
但是思考一下,因为被删除节点向下的所有节点都是平衡的,而你删除节点的规则是固定的,因为这个规则,你会发现不管你怎么删,当前节点往下的节点的平衡因子都是-1,0,或者1。
真正被改变平衡因子的只有被删除的节点及它向上的所有祖先节点,因为对于这些祖先节点来说,你删除了一个节点后,会有节点顶替上来。
对于被删除节点往下的节点来说,不管怎么改变都是0,-1,1这三种变化。因为它们的子树的左右高度差是不变的,所以你删除的节点根本影响不到他们的平衡因子。但是对于祖先节点来说,你顶替上来一个,可能对于整体来说平衡因子就不对了。
所以我们删除节点后,要从被删除节点的位置开始,沿着父节点一路向上回溯,直到根节点。
如果发现存在不平衡了,我们就根据LL,RR,LR,RL型进行调整。
需要注意的是,当某一次检查时发现了第一个不平衡后,调整平衡后要继续向上进行检查是否平衡。
因为左旋右旋这些的本质就是将节点的高度向下移动一个位置,你移动了高度之后,是有可能导致往上的祖先节点失衡的
🌟七、完结

