算法 --- BFS 解决 FloodFill 算法

BFS 解决 FloodFill 算法
BFS 解决的 Flood Fill 算法题目类型是“连通区域”问题,其适用于需要从某个起点开始,向四周(四或八个方向)扩散,并填充或标记所有相连且具有相同属性的相邻点的题目。
为了更清晰地说明,以下是详细的解释:
1. 核心问题类型:连通区域问题
这类问题的本质是:在一个矩阵(二维网格)中,给你一个“起点”和一个“目标值”。你需要找出所有从起点出发,通过上下左右(可能包括斜对角)移动能够到达的、具有初始相同属性的点,并将这些点修改为新的目标值。
这就像图像处理软件中的“油漆桶”工具,你点击一个点,整个相连的同色区域就会被新的颜色填充。
2. 为什么适用 BFS?
-
层序遍历:BFS 非常适合模拟“扩散”过程。从起点开始,像水波纹一样一层一层地向外扩展,确保每次填充的都是当前最近、相邻的点。
-
避免递归栈溢出:对于非常大的网格,DFS 的递归实现可能导致调用栈溢出。而 BFS 使用队列,通常更安全。
-
最短路径:虽然 Flood Fill 本身不要求最短路径,但其扩散的“层”的概念与计算起点到区域内任意点的最短步数天然契合。
3. 适用题目的关键特征:
当你看到一个题目具有以下一个或多个特征时,就应考虑使用 BFS(或 DFS)进行 Flood Fill:
-
数据结构是网格(Grid):题目通常提供一个
m x n的二维数组(字符或数字),代表地图、图像等。 -
操作对象是“区域”:问题要求你计算连通区域的数量、标记一个连通区域、或替换一个连通区域的颜色/数值。
-
移动方向是相邻的:点的连通性定义为上下左右(四连通)或包括对角线(八连通)。
-
起点明确:题目直接指定了开始的坐标
(sr, sc)。
4. 经典例题:
-
图像渲染(Flood Fill):LeetCode 733。
-
题目:有一幅图像用一个
m x n的整数网格表示,给你一个起点(sr, sc)和一个新颜色newColor,让你从起点开始对相连的同色区域进行填充(染色)。 -
为什么适用:完美符合所有特征——网格、连通区域、相邻、起点明确。
-
-
岛屿数量:LeetCode 200。
-
题目:给你一个由
'1'(陆地)和'0'(水)组成的网格,计算其中岛屿的数量。(岛屿被水包围,由水平或垂直方向的陆地相连形成) -
为什么适用:需要遍历网格,每当遇到一块陆地
’1‘,就以其为起点进行 BFS/DFS,将整个相连的岛屿标记为已访问(相当于“填充”为水‘0’)。这样,BFS 的次数就是岛屿的数量。
-
-
被围绕的区域:LeetCode 130。
-
题目:给你一个
m x n的矩阵,由字符'X'和'O'组成。找到所有被'X'围绕的区域,并将这些区域里的所有'O'用'X'填充。 -
为什么适用:策略是从边界上的
’O‘开始进行 Flood Fill,标记所有不会被围绕的’O‘(即与边界连通的)。最后,剩下的未被标记的’O‘就是被围绕的,需要填充。
-
-
腐烂的橘子:LeetCode 994。
-
题目:网格中每个单元格可能有三个值:
0(空)、1(新鲜橘子)、2(腐烂橘子)。每分钟,腐烂橘子会使其相邻的新鲜橘子腐烂。问需要多久才能使所有橘子腐烂。 -
为什么适用:这是一个多起点的 Flood Fill 问题。所有腐烂的橘子都是起点,同时开始向外(BFS)扩散。整个过程所需的“分钟数”就是 BFS 遍历的层数。
-
总结
| 特征 | 描述 | 例子 |
|---|---|---|
| 场景 | 网格、矩阵、地图 | 图像、棋盘、岛屿地图 |
| 操作 | 填充、染色、标记、感染、计算连通块 | 油漆桶工具、计算岛屿数、橘子腐烂 |
| 移动 | 向四周(四方向/八方向)扩散 | 上下左右 |
| 起点 | 单点起点或多点起点 | 一个像素点、多个腐烂源 |
简单来说:只要问题是在网格上“找一块连在一起的地方并对它做点什么事”,BFS Flood Fill 算法大概率就是解决方案。
题目练习
733. 图像渲染 - 力扣(LeetCode)
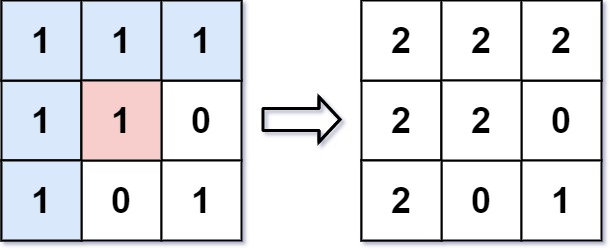
算法思路:
可以利用「深搜」或者「宽搜」,遍历到与该点相连的所有「像素相同的点」,然后将其修改成指定的像素即可。
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {int prev = image[sr][sc];if(prev == color) return image;queue<pair<int, int>> q;int m = image.size(), n = image[0].size();q.push({sr, sc});while(q.size()){auto [x, y] = q.front();q.pop();image[x][y] = color;for(int k = 0; k < 4; ++k){int a = x + dx[k], b = y + dy[k];if(a >= 0 && a < m && b >= 0 && b < n && image[a][b] == prev){q.push({a, b});}}}return image;}
};
200. 岛屿数量 - 力扣(LeetCode)
算法思路:
遍历整个矩阵,每次找到 一块陆地 的时候:
-
说明找到 一个岛屿,记录到最终结果
ret里面; -
并且将这个陆地相连的所有陆地,也就是这块 岛屿,全部 变成海洋。这样的话,我们下次遍历到这块岛屿的时候,它 已经是海洋 了,不会影响最终结果。
-
其中 变成海洋 的操作,可以利用 深搜 和 宽搜 解决,其实就是 733. 图像渲染 这道题~
这样,当我们,遍历完全部的矩阵的时候,ret 存的就是最终结果。
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};bool vis[301][301];//false;queue<pair<int, int>> q;int m, n;void bfs(vector<vector<char>>& grid, int i, int j){vis[i][j] = true;q.push({i,j});while(q.size()){auto [x, y] = q.front();q.pop();for(int k = 0; k < 4; ++k){int a = x + dx[k];int b = y + dy[k];if(a >= 0 && a < m && b >= 0 && b < n && grid[a][b] == '1' && !vis[a][b]){q.push({a, b});vis[a][b] = true;}}}}int numIslands(vector<vector<char>>& grid) {m = grid.size();n = grid[0].size();int ret = 0;for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(grid[i][j] == '1' && !vis[i][j]){bfs(grid, i, j);ret++;}}}return ret;}
};
695. 岛屿的最大面积 - 力扣(LeetCode)
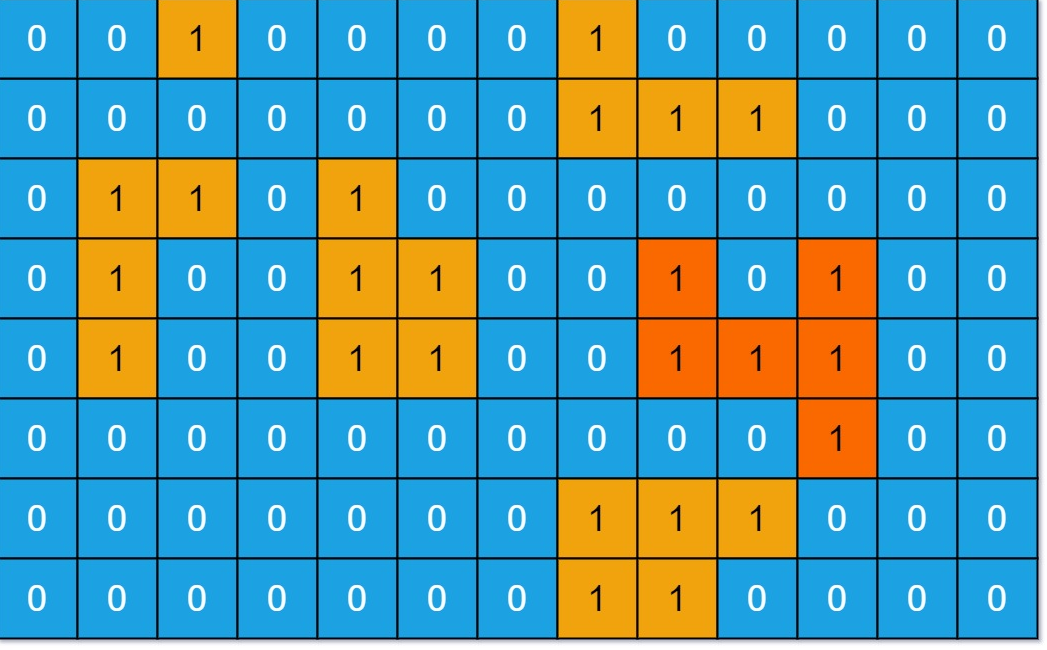
算法思路:
-
遍历整个矩阵,每当遇到一块土地的时候,就用 「深搜」 或者 「宽搜」 将与这块土地相连的 「整个岛屿」 的面积计算出来。
-
然后在搜索得到的 「所有的岛屿面积」 求一个 「最大值」 即可。
-
在搜索过程中,为了 「防止搜到重复的土地」:
-
可以开一个同等规模的 「布尔数组」,标记一下这个位置是否已经被访问过;
-
也可以将原始矩阵的
1修改成0,但是这样操作会修改原始矩阵。
-
class Solution {
public:int ret, m, n;bool vis[51][51];queue<pair<int, int>> q;int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int maxAreaOfIsland(vector<vector<int>>& grid) {m = grid.size(), n = grid[0].size();for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(grid[i][j] == 1 && !vis[i][j]) bfs(grid, i, j);}}return ret;}void bfs(vector<vector<int>>& grid, int i, int j){int tmp = 1;q.push({i, j});vis[i][j] = true;while(q.size()){auto[x, y] = q.front();q.pop();for(int k = 0; k < 4; ++k){int a = x + dx[k], b = y + dy[k];if(a >= 0 && a < m && b >= 0 && b < n && grid[a][b] == 1 && !vis[a][b]){vis[a][b] = true;q.push({a, b});tmp++;}}}ret = max(ret, tmp);}
};
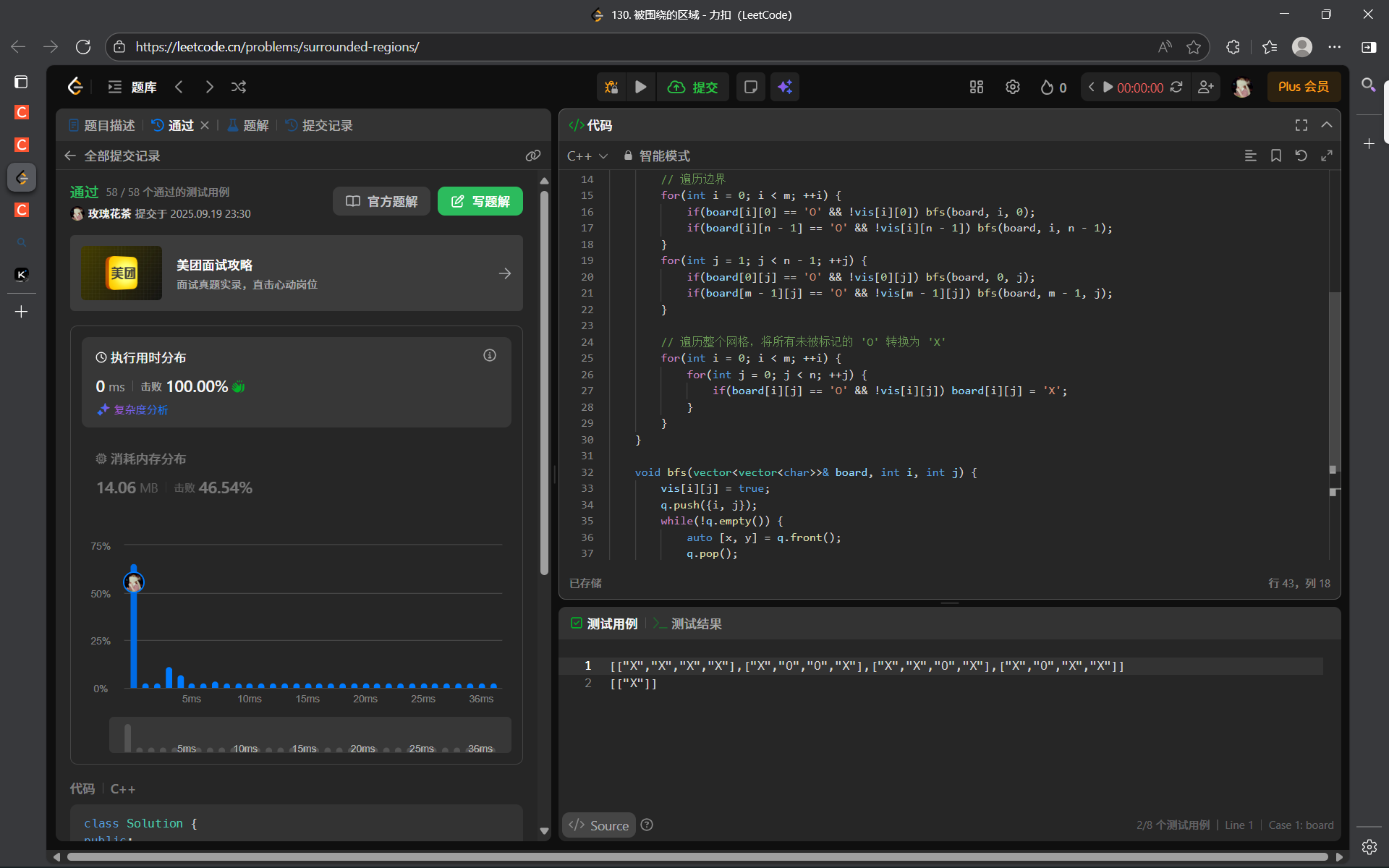
130. 被围绕的区域 - 力扣(LeetCode)
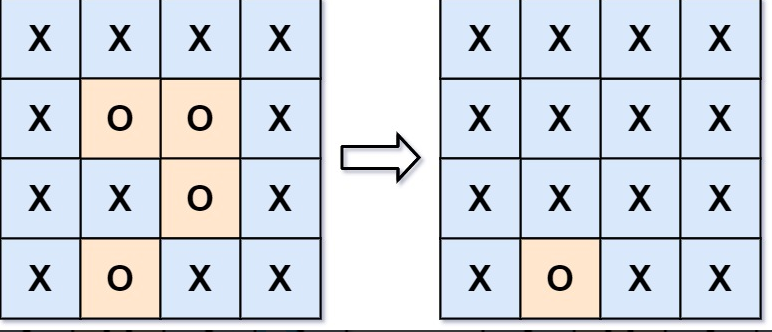
算法思路:
-
正难则反。
-
可以先利用 BFS 将与边缘相连的
'0'区域做上标记,然后重新遍历矩阵,将没有标记过的'0'修改成'1'即可。
class Solution {
public:int m, n;bool vis[201][201];queue<pair<int, int>> q;int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};void solve(vector<vector<char>>& board) {m = board.size(), n = board[0].size();// 初始化vis数组memset(vis, 0, sizeof(vis));// 遍历边界for(int i = 0; i < m; ++i) {if(board[i][0] == 'O' && !vis[i][0]) bfs(board, i, 0);if(board[i][n - 1] == 'O' && !vis[i][n - 1]) bfs(board, i, n - 1);}for(int j = 1; j < n - 1; ++j) {if(board[0][j] == 'O' && !vis[0][j]) bfs(board, 0, j);if(board[m - 1][j] == 'O' && !vis[m - 1][j]) bfs(board, m - 1, j);}// 遍历整个网格,将所有未被标记的 'O' 转换为 'X'for(int i = 0; i < m; ++i) {for(int j = 0; j < n; ++j) {if(board[i][j] == 'O' && !vis[i][j]) board[i][j] = 'X';}}}void bfs(vector<vector<char>>& board, int i, int j) {vis[i][j] = true;q.push({i, j});while(!q.empty()) {auto [x, y] = q.front();q.pop();for(int k = 0; k < 4; ++k) {int a = x + dx[k], b = y + dy[k];if(a >= 0 && a < m && b >= 0 && b < n && board[a][b] == 'O' && !vis[a][b]) {vis[a][b] = true;q.push({a, b});}}}}
};