《智能传感与信息处理》学习1|相机模型

相机模型
参考https://blog.csdn.net/Mapmost/article/details/137781706进行学习

---

我的博客源文件被我删掉了，更新不了了，气死我了。https://brightendavid.github.io/

前言

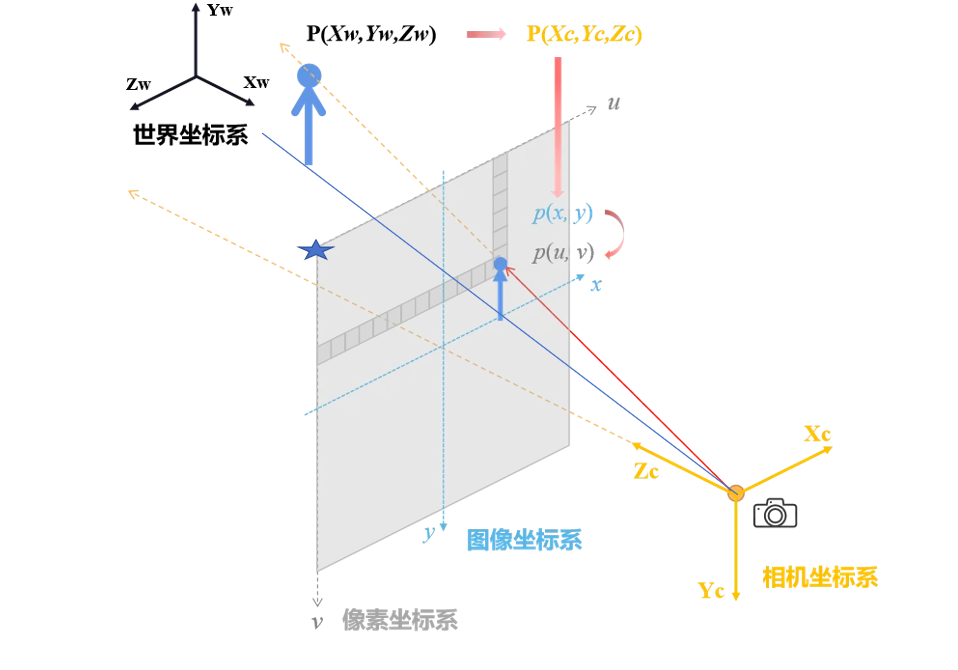
目的：将现实中世界坐标中的点（Xw,Yw,Zw）拍摄到相机中，获得图像坐标，这个坐标是以相机焦点为中心，相机焦距为到相机距离的一个虚拟平面；最后，将这个虚拟平面的坐标起始点移动到图像的左上角，得到了最后的像素坐标。

其中，最重要的知识涉及仿射变换和线性代数的相关知识，坐标系的变换可以说是线性代数的本质应用了。
仿射变换是一个神奇的东西，涉及到二维图像在三维中的变换，变平行四边形什么的

一、世界坐标=》相机坐标

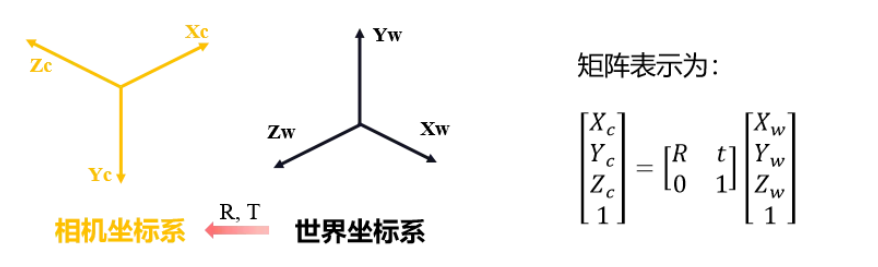
坐标中心是相机镜头，Z轴是距离相机的垂直距离。
最后的矩阵本质上是一个仿射变换，需要旋转矩阵R和平移矩阵T。
因为不能保证相机一定是和世界坐标垂直的，这和坐标建模有一定关系。

这是R，α表示旋转角度。

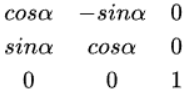
这是平移矩阵T。

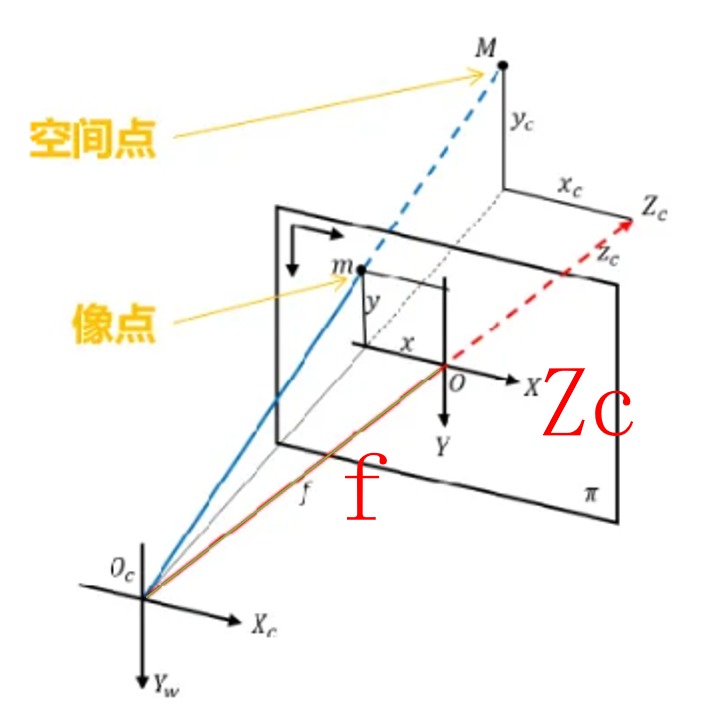
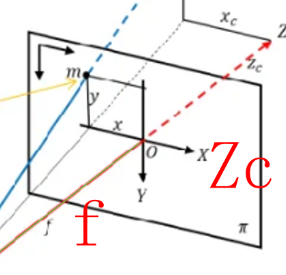
二、相机坐标=》图像坐标

总体就是先根据相似三角形做缩放，再做一个平移+旋转的仿射变换。

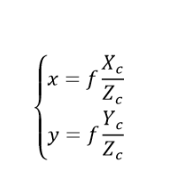
换一种写法就是

Xc / x  =  f / Zc
Yc / y   =  f / Zc

这个东西就是相似三角形对应量等比嘛，高比高，对边比对边。其中，f表示焦距；Zc表示物体的相机坐标。

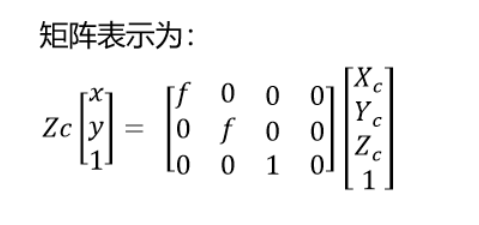
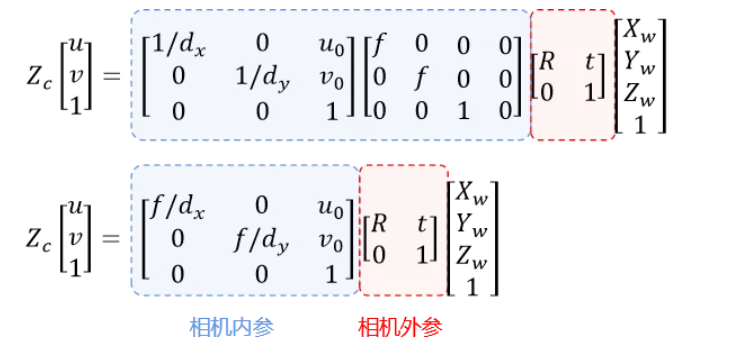
写成矩阵就是这样一个东西，Zc除过去就行了。
现在已经转为了π面的一个图像坐标系了。

三、图像坐标=》像素坐标

现在，需要把坐标原点O转移到图像坐标轴的原点，即图像的左上角。

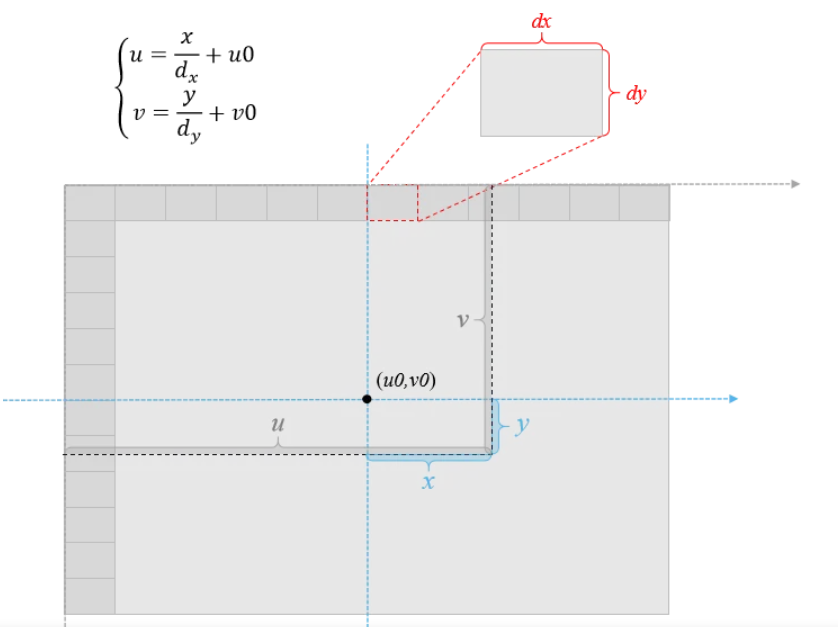
和第一步的原理相同，还是一个仿射变换就可完成了。
和第一步不同，因为涉及到**模拟信号到数字信号（不知道这种说法对不对）**的变换，还需要进行一个缩放变换。

缩放的仿射矩阵

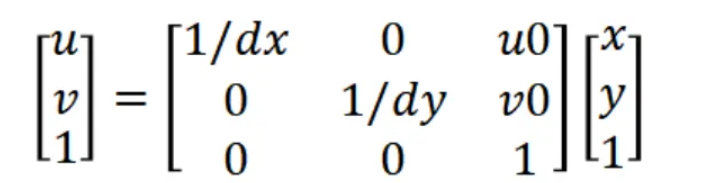
可以看到，这里是不需要做旋转变换的，或者说做变换就在矩阵上加一个负号。
在上述公式中，dx，dy可以理解为地图比例尺的概念。

综上所述

最后就是把三个变换矩阵相乘。