06 一些常用的概念及符号

让我们用通俗易懂的话来解释数据集和函数的概念，并结合具体的例子进行说明。

1 数据集

大白话解释

数据集就像是一个装满各种信息的盒子。这个盒子里有很多小卡片，每张卡片上都记录了一组特定的信息。这些信息可以是关于某个事物的各种属性和对应的标签（结果）。比如，我们有一个数据集，里面包含了很多房子的信息，每张卡片上记录了房子的面积、房间数量等属性，以及这栋房子的价格。

数学表示

数据集 S={zi}i=1n={(xi,yi)}i=1nS = \{\mathbf{z}_i\}_{i=1}^n = \{(\mathbf{x}_i, \mathbf{y}_i)\}_{i=1}^nS={zi​}i=1n​={(xi​,yi​)}i=1n​ 从一个定义在域 $\mathcal{Z}=\mathcal{X}\times \mathcal{Y}$上的分布$\mathcal{D}$ 中采样得到。

• ${\mathbf{x}}_i$ 表示第 $i$ 个样本的特征向量，比如房子的面积、房间数量等。
• ${\mathbf{y}}_i$ 表示第 $i$ 个样本的标签，比如房子的价格。
• $n$ 是样本的数量。

具体例子

假设我们有一个数据集，包含以下几条记录：

房子面积 (平方米)	房间数量	房子价格 (万元)
80	2	350
120	3	540
90	2	420

在这个例子中：

• ${\mathbf{x}}_1=(80,2)$，${\mathbf{y}}_1=350$
• ${\mathbf{x}}_2=(120,3)$，${\mathbf{y}}_2=540$
• ${\mathbf{x}}_3=(90,2)$，${\mathbf{y}}_3=420$

2 函数

大白话解释

函数就像是一个神奇的机器，它可以根据输入的信息计算出相应的输出结果。在机器学习中，我们希望找到一个合适的函数，能够根据给定的特征（输入）准确地预测出标签（输出）。比如，我们希望通过房子的面积和房间数量（输入），准确地预测出房子的价格（输出）。

数学表示

如果存在一个目标函数，它表示为 $f^{\ast }$ 或 $f:\mathcal{X}\to \mathcal{Y}$，满足${\mathbf{y}}_i=f^{\ast }({\mathbf{x}}_i)$ 对于 $i=1,\dots ,n$。

假设空间用 $\mathcal{H}$表示。假设函数表示为 $f_{\theta }(\mathbf{x})\in \mathcal{H}$ 或 $f(\mathbf{x};\theta )\in \mathcal{H}$，其中 $f_{\theta }:\mathcal{X}\to \mathcal{Y}$。

$\theta$ 表示 $f_{\theta }$ 的参数集。

具体例子

继续上面的房子价格的例子，我们希望找到一个函数 ( f )，能够根据房子的面积和房间数量预测出房子的价格。

假设我们找到了一个简单的线性函数：
$$f(\mathbf{x})=w_1\cdot \text{面积}+w_2\cdot \text{房间数量}+b$$

其中$w_1$、$w_2$ 和$b$ 是我们需要学习的参数（即 $\theta$）。

通过训练数据集，我们可以调整这些参数，使得函数$f$ 能够尽可能准确地预测房子的价格。例如，经过训练后，我们可能得到：
$$f(\mathbf{x})=3.5\cdot \text{面积}+20\cdot \text{房间数量}+50$$

这样，当我们输入一个新的房子的面积和房间数量时，就可以用这个函数来预测它的价格了。

3 损失函数

🎯 核心一句话：

损失函数就是模型的“错题本”和“打分器”——它告诉模型：你这次预测得有多离谱。

就像考试时，你答错了题，老师会扣分。损失函数就是给模型每次预测“扣分”的规则。

---

3.1 大白话解释

想象你在学做菜，师傅给你一个菜谱（这就是模型），你按菜谱炒了一盘菜（这是你的预测），然后师傅尝了一口，评价说：“太咸了！” 或 “火候刚好！”

• 损失函数 就是那个评价标准。
  • 如果你说这道菜应该是“辣的”，但其实它是“甜的”，那你就“错得离谱”，损失就高。
  • 如果你说是“微辣”，实际是“中辣”，那还凑合，损失就低一点。
  • 如果完全对上了，损失就是0。

它的目的就是：量化错误的程度，让模型知道自己哪里做得不好，然后去改进。

---

3.2 数学表示

损失函数是一个数学工具，形式化地定义这种“错误程度”。

$$\ell :\mathcal{H}\times \mathcal{Z}\to {\mathbb{R}}_{+}:=[0,+\infty )$$

意思是： 输入是“一个模型 $f_{\theta }$” 和 “一个真实样本 $z=(x,y)$”，输出是一个非负数（越大表示错得越厉害）。

---

3.3 举个具体例子：预测房价

假设你要预测房子的价格：

房子面积	真实价格 $y$	模型预测价格 $f_{\theta }(x)$
80㎡	350 万元	380 万元

模型猜贵了30万。那它该扣多少分？这就看用什么“评分标准”（损失函数）了。

✅ 常见损失函数1：平方损失（L² Loss）

这是最常用的损失函数，特别适合回归问题（预测连续值）。

公式：
$$\ell (f_{\theta },z)=\frac{1}{2}(f_{\theta }(x)-y{)}^2$$

代入上面的例子：
$$\ell =\frac{1}{2}(380-350{)}^2=\frac{1}{2}\times 900=450$$

👉 错30万，扣450分。注意这里是平方，所以错得越多，扣分呈爆炸式增长（错60万要扣1800分！），这样能狠狠惩罚大错误。

注：前面的 $\frac{1}{2}$ 是为了求导方便，不影响结果趋势。

---

✅ 常见损失函数2：绝对损失（L¹ Loss）

另一种更“温和”的方式：

$$\ell =|f_{\theta }(x)-y|$$

在上面的例子中：
$$\ell =|380-350|=30$$

👉 直接按差值扣分，不会因为误差大而惩罚过重。

---

3.4 从单个样本到整个数据集：经验风险（训练损失）

光看一道题的错题不够，要看整张卷子的总分。

所以我们把所有样本的损失加起来，求平均，得到训练损失：

$$L_S(\theta )=\frac{1}{n}\sum _{i=1}^n\ell (f_{\theta }(x_i),y_i)\text{\hspace{1em}(11)}$$

这叫经验风险，也就是模型在整个训练集上的“平均扣分”。

模型的目标就是：不断调整自己的参数 $\theta$，让这个总分（损失）越来越小，直到几乎不扣分（完美拟合）。

---

3.5 理想 vs 现实：总体风险

上面的 $L_S(\theta )$ 只是对训练集的评价。我们真正关心的是模型在未来没见过的数据上表现如何。

这叫总体风险（期望损失）：

$$L_{\mathcal{D}}(\theta )={\mathbb{E}}_{\mathcal{D}}\ell (f_{\theta }(x),y)\text{\hspace{1em}(12)}$$

意思是：在所有可能的数据（服从分布 $\mathcal{D}$）上，模型的平均错误程度。

可惜，$\mathcal{D}$ 是未知的，所以我们只能用训练集上的 $L_S(\theta )$ 来估计它。

---

✅ 总结：损失函数到底是什么？

角色	说明
裁判员	给模型的每次预测打分，分数越高表示错得越离谱
导航仪	告诉模型“往哪个方向调整参数”能让错误减少（梯度下降靠它指路）
目标函数	训练过程就是在最小化损失函数 $L_S(\theta )$

🎯 所以，选对损失函数，就像选对了“好学生”的标准。

• 你用平方损失，模型就会努力避免大错误；
• 你用绝对损失，模型对异常值更鲁棒。

这就是为什么我们需要损失函数——没有它，模型就像蒙眼走路，根本不知道自己走没走对。

4 一些常用的激活函数

激活函数在神经网络中扮演着至关重要的角色。它们被用来引入非线性因素，使得模型可以学习和表示更加复杂的数据模式。下面我将用简单易懂的语言解释几种常见的激活函数。

4.1 Sigmoid 函数

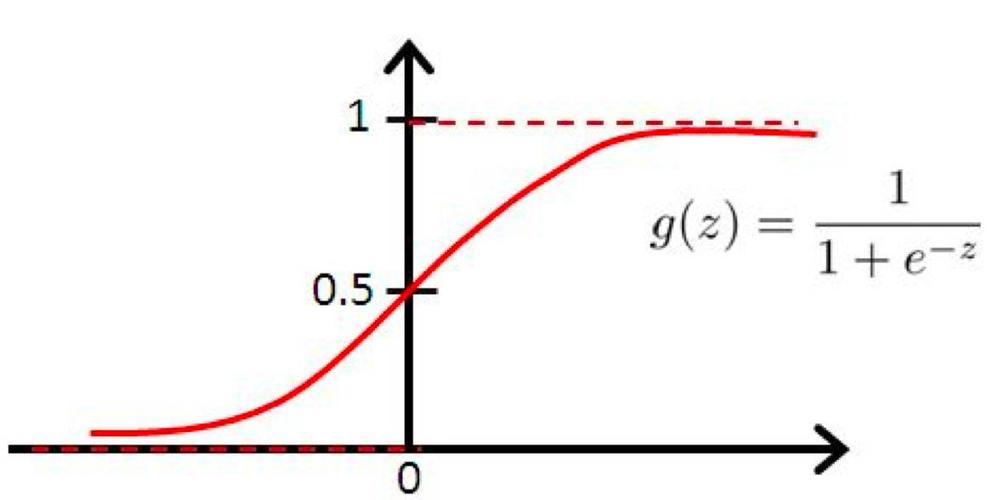
Sigmoid 函数是一种将输入值映射到0和1之间的函数。它特别适合用于二分类问题的输出层，因为它可以把预测结果解读为概率。

公式：
$$\sigma (x)=\text{sigmoid}(x)=\frac{1}{1+e^{-x}};$$

4.2 Tanh 函数（双曲正切）

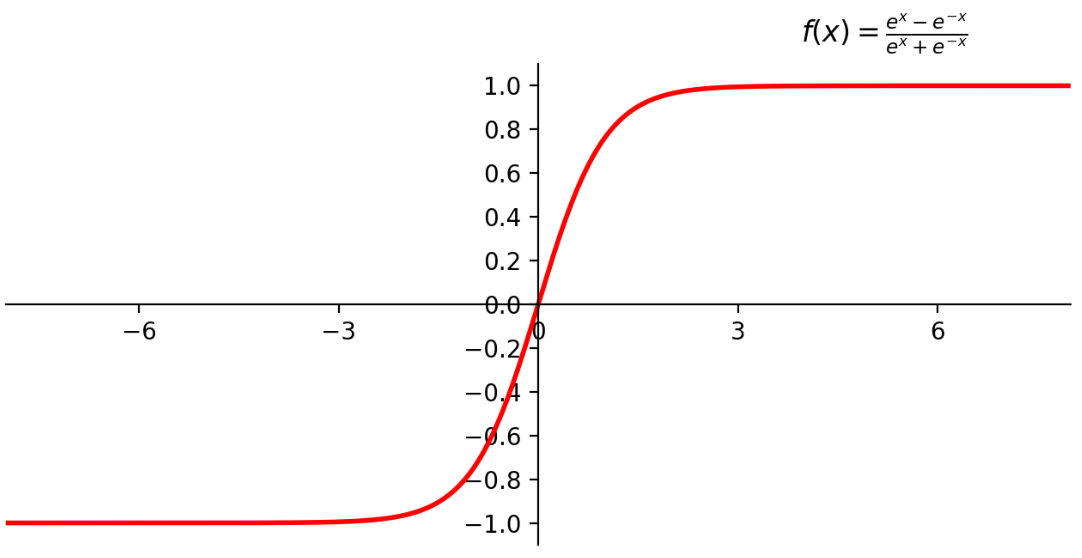
Tanh 函数类似于 Sigmoid 函数，但它的输出范围是-1到1之间。这有助于数据的中心化，可能加速训练过程中的收敛速度。

公式：
$$\sigma (x)=\tanh (x);$$

4.3 三角函数（如cos, sin）

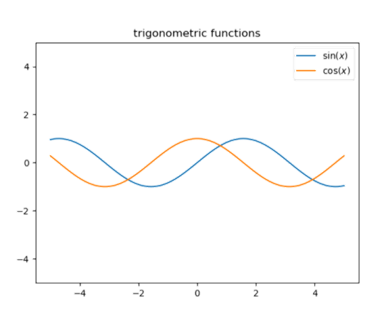
虽然在神经网络中不常用，但在特定情况下，三角函数也能作为激活函数使用。这些函数通常会产生周期性的输出，对于模拟周期性行为很有帮助。

公式：
$$\sigma (x)=\cos x,\sin x;$$

4.4 ReLU 函数（修正线性单元）

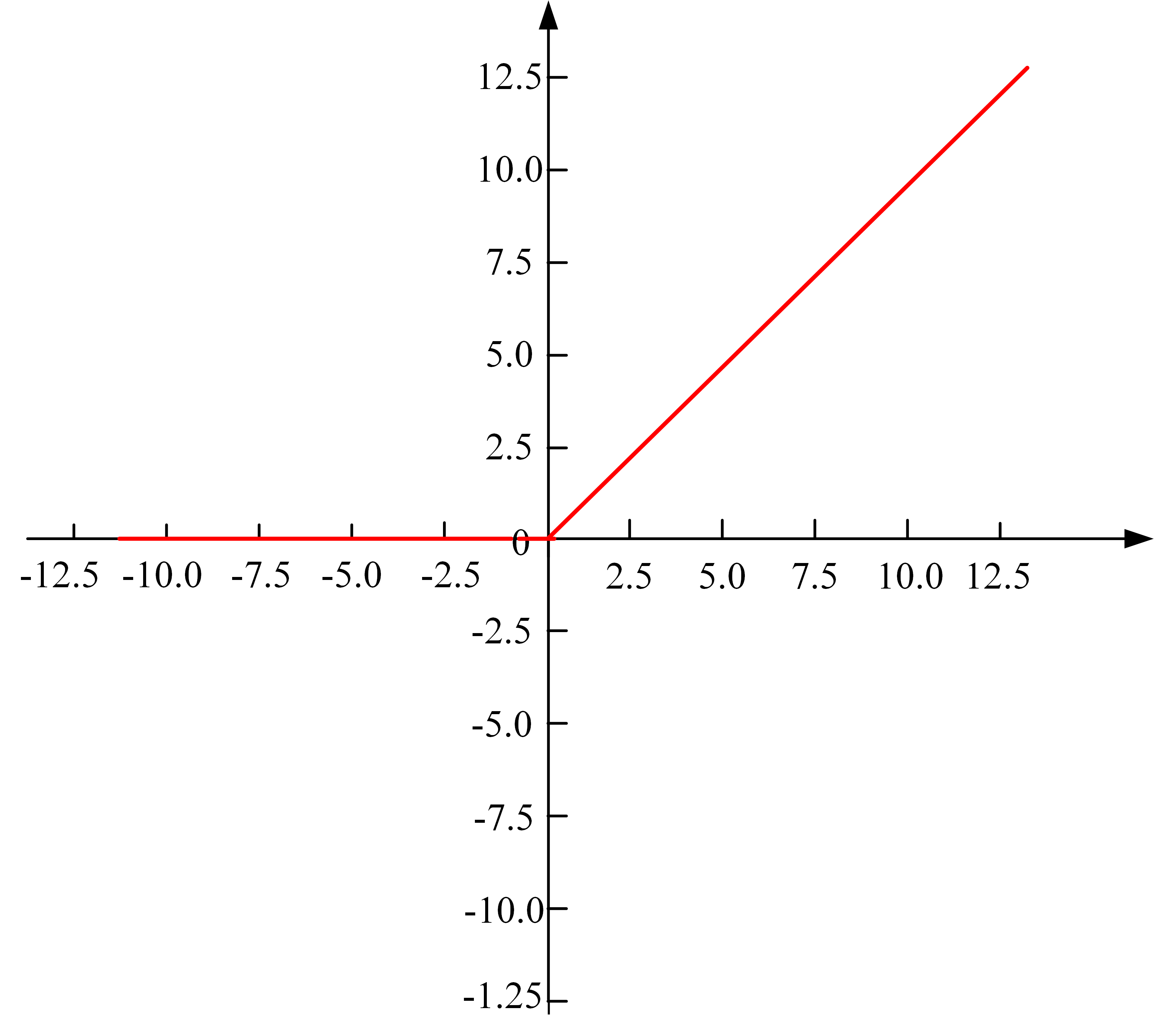
ReLU 是目前最受欢迎的激活函数之一。它非常简单，如果输入大于0，就返回该输入；如果输入小于或等于0，则返回0。这种简单的操作使得计算效率非常高，而且能有效缓解梯度消失的问题。

公式：
$$\sigma (x)=\text{ReLU}(x)=\max (0,x);$$

4.5 举例说明

假设我们正在构建一个识别手写数字的神经网络。在网络的隐藏层中，我们可以使用 ReLU 激活函数来增加模型的非线性表达能力。然后，在输出层，为了得到每个数字的概率分布，我们可以选择 Sigmoid 函数（对于二分类）或者 Softmax 函数（对于多分类）。这样，通过激活函数的帮助，我们的模型能够更准确地对手写数字进行分类。

记住，选择哪种激活函数取决于具体的应用场景以及你想要解决的问题类型。不同的激活函数适用于不同类型的任务。