分治——归并排序算法题

首先我们先借助一个排序题来回顾一下归并排序

1.排序数组

归并排序也是基于分治策略的排序算法，包含“划分”和“合并”两个阶段。

1.划分阶段：基于数组的中间元素，将数组划分为两个区间，通过不断递归，将长数组排序问题转化为短数组排序问题

2.合并阶段：当划分之后的数组只有一个元素时开始合并，持续地将左右两个较短的有序数组合并为一个较长的有序数组，直至结束。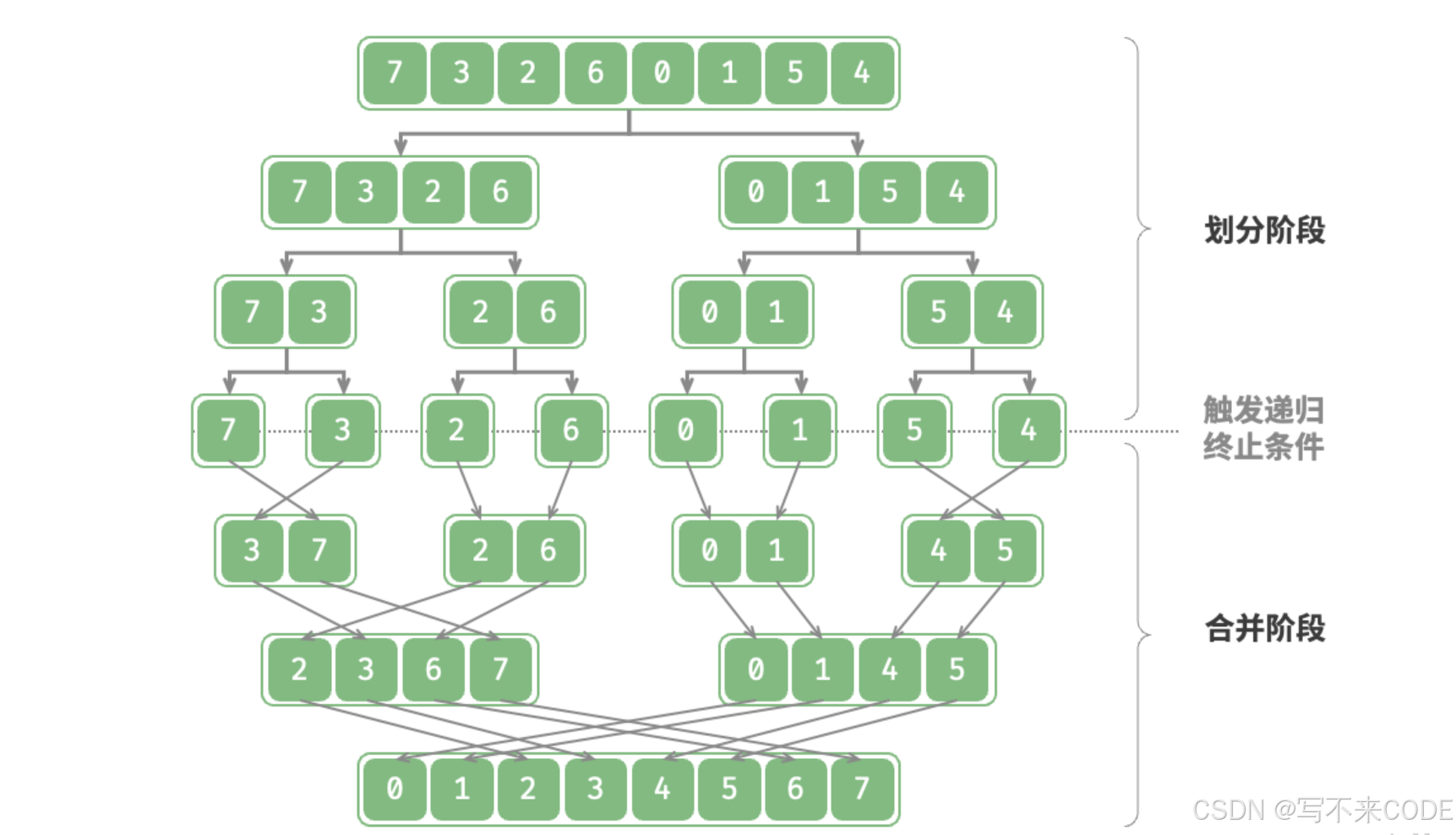

归并排序的过程就类似于二叉树的后序遍历，先递归展开左子树，然后展开右子树，最后在访问根节点。

在合并阶段，我们无法在原数组进行合并，需要借助一个临时数组tmp，将合并后的结果先存放到tmp中，接着将tmp的有序数组拷贝回原数组中。然后返回上一层，继续进行归并操作。

但是如果我们在合并操作的栈帧中创建临时数组tmp的话，需要不断的进行数组的创建销毁。这也是一笔开销。所以我们最好创建一个全局的tmp，大小就与原数组相同。这样就不会频繁的申请和释放内存了。

时间复杂度：O(nlogn)，递归的深度是logn，每一层需要遍历这个子数组就是n

空间复杂度：O(n)，递归使用的栈空间的开销为O(logn)，合并两个有序数组借助的临时数组tmp消耗O(n)

// C++

class Solution 
{
    vector<int> tmp;
public:
    void merge(vector<int>& nums,int l, int mid, int r)
    {
        // [l,mid] [mid+1,r]
        int i = l, j = mid+1, k = 0;
        while(i<=mid && j<=r)
        {
            if(nums[i] < nums[j]) tmp[k++] = nums[i++];
            else tmp[k++] = nums[j++];
        }
        // 循环结束只将一个区间的全部元素插入到tmp中
        // 判断那个区间还有元素，直接将剩余元素都插入到tmp即可
        while(i<=mid) tmp[k++] = (nums[i++]);
        while(j<=r) tmp[k++] = (nums[j++]);

        for(int p=l; p<=r; p++) nums[p] = tmp[p-l];
    }

    void merge_sort(vector<int>& nums, int l, int r)
    {
        if(l >= r) return;

        // 选择中间点
        int mid = (r - l) / 2 + l; // 防溢出

        //[l, mid] [mid+1, r]
        merge_sort(nums,l,mid);
        merge_sort(nums,mid+1,r);

        // 合并两个有序数组
        merge(nums, l, mid, r);
    }

    vector<int> sortArray(vector<int>& nums) 
    {
        tmp.resize(nums.size());
        merge_sort(nums, 0, nums.size()-1);    
        return nums;
    }
};

 2.交易逆序对的总数

前一个数大于后一个数，就称为是一个逆序对。题目需要我们找出所有逆序对的数目。

解法1：暴力枚举

定义计数器count，两层for循环枚举出所有的数对，如果数对满足要求就count++。返回count即可。 

时间复杂度：O(n^2)，运行会导致超出时长限制

空间复杂度：O(1)

解法2：分治策略，借助归并思想

对于这整个数组的逆序对来说，我们可以分开来求其每个部分的逆序对，最后加起来即可。

我们拿示例来验证一下这个方法是否成立：很显然，这个方法是可以成立的。接下来就是如果实现这个算法：如果我们将逆序对采取分开计算，但是在每个区间我们如果继续采取遍历的方式计算逆序对的话，时间复杂度甚至比直接暴力枚举还低。所有在我们决定分开计算逆序对后还需要根据其中的规律，避免出现枚举全部结果的行为。

        策略1：我们在统计完左区间和右区间的逆序对之后，在统计一左一右的逆序对时先对左右两个区间进行排序。首先，对这两个区间排序是不会影响一左一右的结果的。我们排升序数组，然后在右区间找前面有几个数比我大。

当我们排升序数组之后，在计算一左一右时，如果nums[i] < = nums[j]，说明选i位置的元素是无法构成逆序对的。我们让i位置的元素进临时数组tmp，并且i++，选择下一个左元素；

当nums[i] > nums[j]时，此时i位置的元素满足逆序对。而且对于i+1~mid的所有数来说，他们都大于nums[i] ，所以他们都可以与j位置的元素构成逆序对。此时我们就可以统计许多逆序对：ret += mid - i + 1.同时不要忘了将j位置的元素放入tmp中。

需要注意的是，在第二种情况下，我们只需要让j++，i不用动。

那么我们想：找前面有几个数比我大可不可以是在降序数组的基础上呢？不行！

        策略2：与策略1一致，只不过在排序的时候排成降序，接着我们在后面找多少个元素比我小。nums[i] <= nums[j]，此时让tmp[k++] = nums[j++] ；nums[i]  > nums[j]，此时i位置和j位置满足逆序对，且因为数组是逆序，所以j位置的元素大于j之后的所有元素，所以我们可以直接统计一大片结果，ret += right - j + 1，接着让tmp[k++] = nums[i++].

同样的，找后面有多少个比我小不可以用升序，否则会重复计算。

时间复杂度：O(nlogn)，实际上述的过程就是归并排序的过程

空间复杂度：O(n)，临时数组tmp

// C++

class Solution 
{
    vector<int> tmp;
public:
    // 策略一：升序数组，找前面有几个比我大的
    int mergeInGreater(vector<int>& nums, int l, int mid, int r)
    {
        // [l,mid] [mid+1,r]
        int ret = 0, i = l, j = mid + 1, k = 0;
        while(i<=mid && j<=r)
        {
            if(nums[i]<=nums[j]) tmp[k++] = nums[i++];
            else
            {
                ret += mid - i + 1;
                tmp[k++] = nums[j++];
            }
        }
        while(i<=mid) tmp[k++] = nums[i++];
        while(j<=r) tmp[k++] = nums[j++];

        for(int p=l; p<=r; p++) nums[p] = tmp[p-l];

        return ret;
    }

    // 策略二：降序数组，找后面有几个比我小的
    int mergeInLess(vector<int>& nums, int l, int mid, int r)
    {
        // [l,mid] [mid+1,r]
        int ret = 0, i = l, j = mid + 1, k = 0;
        while(i<=mid && j<=r)
        {
            if(nums[i]<=nums[j]) tmp[k++] = nums[j++];
            else
            {
                ret += r - j + 1;
                tmp[k++] = nums[i++];
            }
        }
        while(i<=mid) tmp[k++] = nums[i++];
        while(j<=r) tmp[k++] = nums[j++];

        for(int p=l; p<=r; p++) nums[p] = tmp[p-l];

        return ret;
    }

    int merge_sort(vector<int>& nums, int l, int r)
    {
        if (l>=r) return 0;

        int mid = (r - l) / 2 + l;
        // [l,mid] [mid+1,r]

        // 升序
        //return merge_sort(nums,l,mid) + merge_sort(nums,mid+1,r) + mergeInGreater(nums,l,mid,r);

        // 降序
        return merge_sort(nums,l,mid) + merge_sort(nums,mid+1,r) + mergeInLess(nums,l,mid,r);

    }

    int reversePairs(vector<int>& record) 
    {
        tmp.resize(record.size());
        return merge_sort(record, 0, record.size()-1);
    }
};

3.计算右侧小于当前元素的个数

 给一个数组nums，我们需要返回一个与该数组一样大的数组ret，ret的每一个元素是对应nums元素中右侧小于该元素的个数。

解法1：暴力枚举

定义计数器count，遍历数组nums的同时，再套一层，遍历该元素后面的元素统计有多少个比他小，统计完成后将计数器插入到ret返回数组中。

时间复杂度：O(n^2)，超过时间限制

空间复杂度：O(1)，除了待返回的ret数组，没有额外开销

解法2：分治策略——归并排序

这道题其实和逆序对那道题非常相似。我们将示例1的ret数组加起来就是原数组的逆序对的数量。只不过我们要求出每一个元素的逆序对。

我们可以采取策略2：降序数组，找后面有多少个比我小。但是其中有一个问题，我们不能直接返回ret，而是要将ret加到该元素对应的位置上。但是我们在合并的过程中进行了排序，会打乱原数组的顺序，导致下标对应不上。 

解决方案：在进行归并排序之前，我们先定义一个index数组，存储原数组每个元素对应的下标，当进行合并的同时，让index数组也进行合并，两者同时变化就可以保证下标的对应关系。

运行逻辑：

时间复杂度：O(nlogn)，本质上也是归并排序

空间复杂度：O(n)，需要额外开辟index数组以及两个tmp数组用来辅助nums数组和index数组的合并过程

// C++

class Solution
{
    vector<int> tmp1;// 临时存储nums
    vector<int> tmp2;// 临时存储index
    vector<int> index;// 数组元素是nums对应元素的下标
    vector<int> ret;
public:
    // 降序，在后面找有多少个比我小
    void mergeInLess(vector<int>& nums, int l, int mid, int r)
    {
        // 合并有序数组
        // index数组也要合并，保证nums与index的对应关系
        int i = l, j = mid + 1, k = 0;
        while (i <= mid && j <= r)
        {
            if (nums[i] <= nums[j])
            {
                tmp1[k] = nums[j];
                tmp2[k++] = index[j++];
            }
            else
            {
                ret[index[i]] += r - j + 1;
                tmp1[k] = nums[i];
                tmp2[k++] = index[i++];
            }
        }

        while (i <= mid)
        {
            tmp1[k] = nums[i];
            tmp2[k++] = index[i++];
        }

        while (j <= r)
        {
            tmp1[k] = nums[j];
            tmp2[k++] = index[j++];
        }

        // 覆盖原数组
        for (int p = l; p <= r; p++)
        {
            nums[p] = tmp1[p - l];
            index[p] = tmp2[p - l];
        }
    }

    void merge_sort(vector<int>& nums, int l, int r)
    {
        if (l >= r) return ;

        int mid = (r-l)/2+l;
        // [l,mid] [mid+1,r]
        merge_sort(nums, l, mid);
        merge_sort(nums, mid + 1, r);

        mergeInLess(nums, l, mid, r);
    }

    vector<int> countSmaller(vector<int>& nums)
    {
        if(nums.size() == 1) return {0};

        tmp1.resize(nums.size());
        tmp2.resize(nums.size());
        index.resize(nums.size());
        ret.resize(nums.size());
        for (int i = 0; i < nums.size(); ++i) index[i] = i;

        merge_sort(nums, 0, nums.size() - 1);
        return ret;
    }
};

 4.翻转对

 翻转对的概念就是在原数组中，前面的数如果大于后面的数的二倍，则说明这两个数构成一个翻转对。我们需要返回数组中所有的翻转对。

解法1：暴力枚举

两层for循环枚举出所有的数对，判断其中符合要求的数对，返回其结果即可。该解法会超时

时间复杂度：O(n^2)

空间复杂度：O(1)

解法二：分治——归并排序

我们可以将数组分为左右两个子区间，先统计左边区间满足要求的数对，在统计右边区间满足要求的数对，最后在统计一左一右的情况中满足要求的数对即可。

统计一左一右的结果我们既可以采取策略1：找前面有多少个比我的2倍大，升序数组；策略2：找后面有多少个元素的二倍比我还小，降序数组

这两个策略的修改还是很简单的，这里我们用策略2来实现：

我们在计算一左一右时，尽量不要在合并的同时计算翻转对，这样会导致合并的逻辑变得复杂，我们可以在处理完左右区间之后，先计算这两个有序数组的翻转对，然后在合并数组。

计算两个降序数组的翻转对个数我们可以使用双指针+规律来实现，时间复杂度为O(n).

时间复杂度：O(nlogn)

空间复杂度：O(n)

// C++

class Solution 
{
    vector<int> tmp;
public:
    void mergeInLess(vector<int>& nums, int left, int mid, int right)
    {
        // 借助tmp排序区间
        int i = left, j = mid+1, k = 0;
        while(i<=mid && j<=right) // 降序
        {
            if(nums[i] <= nums[j]) tmp[k++] = nums[j++];
            else// nums[i] > nums[j]
            {
                tmp[k++] = nums[i++];
            }
        }

        // 处理没有排序的区间
        while(i<=mid) tmp[k++] = nums[i++];
        while(j<=right) tmp[k++] = nums[j++];

        // 覆盖原数组，使原数组有序
        for(int i=left; i<=right; ++i)
            nums[i] = tmp[i-left];
    }

    int getreversePairs(vector<int>& nums, int left, int mid, int right)
    {
        // 双指针
        int ret = 0;
        int left_index=left, right_index=mid+1;
        while(left_index <= mid) // 降序
        {
            while(right_index <= right && nums[left_index] / 2.0 <= nums[right_index]) right_index++;
            if(right_index > right)
                break;
            ret += right - right_index + 1;
            left_index++;
        }
        return ret;
    }

    int merge_sort(vector<int>& nums, int left, int right)
    {
        if(left>=right) return 0;
        int ret = 0;

        // 划分区间
        // [left,mid] [mid+1,right]
        int mid = (right-left)/2+left;

        // 处理左区间
        ret += merge_sort(nums,left,mid);

        // 处理右区间
        ret += merge_sort(nums,mid+1,right);

        //获取翻转对
        ret += getreversePairs(nums, left, mid, right);

        // 合并有序数组
        mergeInLess(nums, left, mid, right);

        return ret;
    }

    int reversePairs(vector<int>& nums) 
    {
        tmp.resize(nums.size());
        return merge_sort(nums, 0, nums.size() - 1);
    }
};