人工智能学习:什么是GRU模型

一、GRU介绍
GRU(Gated Recurrent Unit)也称为门控循环单元,是一种改进版的RNN。同LSTM一样能够有效捕捉长序列之间的语义关联,通过引入两个”门”机制(重置门和更新门)来控制信息的流动,从而避免了传统RNN中的梯度消失问题,并减少了LSTM模型中的复杂性。
通过引入更新门 (Update Gate) 和重置门 (Reset Gate) 来控制信息在网络中的流动。这些门控机制决定哪些信息应该保留、哪些信息应该丢弃,从而有效地捕获长距离的依赖关系。
1、内部结构
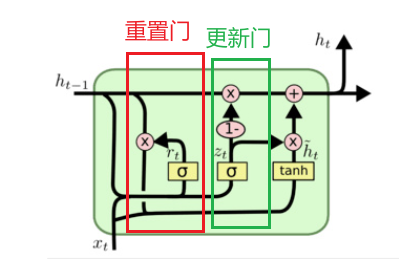
隐藏状态:包含了过去时间步的记忆,并随着时间步的推移不断更新。
重置门:决定在计算候选隐藏状态时,要忽略多少先前的隐藏状态。
更新门:决定在多大程度上保留先前的隐藏状态,以及在多大程度上更新为新的隐藏状态。
候选隐藏状态:基于当前输入和经过重置门过滤后的前一时刻隐藏状态计算出的新的隐藏状态的候选值。
更新后的隐藏状态:最终的隐藏状态,由先前的隐藏状态和候选隐藏状态加权求和得到。
① 重置门(Reset Gate)
决定如何将新的输入与之前的隐藏状态结合。
- 当重置门值接近0时,表示当前时刻的输入几乎不依赖上一时刻的隐藏状态。
- 当重置门值接近1时,表示当前时刻的输入几乎完全依赖上一时刻的隐藏状态。
公式:
rt=σ(Wr⋅[ht−1,xt]+br)
- rt:重置门的输出
- Wr 和 br:重置门的权重和偏置
- σ:sigmoid函数,输出值在 0 到 1 之间
② 更新门(Update Gate)
决定多少之前的信息需要保留,多少新的信息需要更新。
- 当更新门值接近0时,意味着网络只记住旧的隐藏状态,几乎没有新的信息。
- 当更新门值接近1时,意味着网络更倾向于使用新的隐藏状态,记住当前输入的信息。
公式:
zt=σ(Wz⋅[ht−1,xt]+bz)
- zt:更新门的输出
- Wz 和 bz:更新门的权重和偏置
- σ:sigmoid函数,输出值在 0 到 1 之间
③ 候选隐藏状态(Candidate Hidden State)
捕捉当前时间步的信息,多少前一隐藏状态的信息被保留。
公式:
h~t=tanh(Wh⋅[rt⊙ht−1,xt]+bh)
- h~t:候选隐藏状态
- Wh 和 bh:候选隐藏状态的权重和偏置
- tanh:双曲正切函数,用于将值压缩到 -1 到 1 之间
- ⊙:逐元素乘法
④ 最终隐藏状态(Final Hidden State)
控制信息更新,传递长期依赖。
公式:
ht=(1−zt)⊙ht−1+zt⊙h~t
- ht:当前时间步的隐藏状态
- zt:更新门的输出,控制新旧信息的比例
- ⊙:逐元素乘法
