当前位置：首页 > news >正文

C++算法专题学习——分治

news 2025/9/6 7:50:09

本期C++算法专题中我们将学习C++的另一个算法思想策略：分治

相关代码已经上传至作者的个人gitee：楼田莉子/C++算法学习，喜欢请点个赞谢谢

分治介绍

1. 分解（Divide）

2. 解决（Conquer）

3. 合并（Combine）

经典应用场景

分治算法的特点

1、颜色分类

2、排序数组（快速排序）

3、数组中第K个最大的元素

4、最小的K个数字

算法一：排序

算法思路

时间复杂度

算法二：堆

算法思路

时间复杂度

算法三：快速选择

5、排序数组（归并排序）

6、数组中的逆序对

7、计算右侧小于当前元素的个数

8、翻转对

分治介绍

分治（Divide and Conquer）是一种重要的算法设计策略，其核心思想是将一个复杂的问题分解为若干个规模较小但结构与原问题相似的子问题，递归地解决这些子问题，然后将子问题的解合并得到原问题的解。分治算法通常包含三个步骤：

1. 分解（Divide）

将原问题分解为若干个规模较小的子问题。这些子问题应该是相互独立的，并且与原问题形式相同，只是规模更小。例如，在归并排序中，将待排序数组递归地分成两个子数组，直到每个子数组只包含一个元素。

2. 解决（Conquer）

递归地求解子问题。如果子问题的规模足够小，可以直接求解。例如，在归并排序中，当子数组长度为1时，可以直接视为已排序。

3. 合并（Combine）

将子问题的解合并成原问题的解。这一步是分治算法的关键，需要根据具体问题设计合适的合并策略。例如，归并排序在合并两个已排序的子数组时，通过逐个比较元素的大小，将它们按顺序合并为一个有序数组。

经典应用场景

归并排序（Merge Sort）
将数组分成两半，递归排序后再合并。时间复杂度为O(n log n)，是分治算法的典型应用。
快速排序（Quick Sort）
选择一个基准元素，将数组分成小于基准和大于基准的两部分，递归排序。平均时间复杂度为O(n log n)。
二分查找（Binary Search）
在有序数组中查找目标元素，每次将搜索范围减半，时间复杂度为O(log n)。
大整数乘法（Karatsuba算法）
通过分治策略将大整数乘法分解为更小的乘法问题，显著提高计算效率。
最近点对问题
在平面上的点集中找到距离最近的一对点，通过分治法可以将时间复杂度优化到O(n log n)。

分治算法的特点

适用条件：问题可以分解为独立的子问题，且子问题的解可以合并为原问题的解。
效率：通常能显著降低时间复杂度，如从O(n²)优化到O(n log n)。
缺点：递归调用可能导致额外的空间开销，且合并步骤的设计可能较为复杂。

1、颜色分类

算法思想：三指针。类似于这道题：283. 移动零 - 力扣（LeetCode）

1、left标记0区域最右侧、right标记2区域最左侧、i遍历数组

[0,left]：全是0

[letf+1,i-1]：全是1

[i,right-1]：待扫描的元素

[right,n-1]：全是2

2、分类讨论

如果nums[i]为0，left++,交换nums[left]和nums[i]，i++；

如果nums[i]为1，i++；

如果nums[i]为2，right--,交换nums[right]和nums[i]；(因为后面是待扫描的元素，所以i不能++)

class Solution {
public:void sortColors(vector<int>& nums) {int n=nums.size();int left=-1,right=n,i=0;while(i<right){if(nums[i]==0) swap(nums[++left],nums[i++]);else if(nums[i]==1) i++;else if(nums[i]==2) swap(nums[--right],nums[i]);}}
};

2、排序数组（快速排序）

算法思想：快速排序

1、数组分三块实现快排。类似于颜色分类

2、分类讨论

如果nums[i]<key，left++,交换nums[left]和nums[i]，i++；

如果nums[i]=key，i++；

如果nums[i]>key，right--,交换nums[right]和nums[i]；(因为后面是待扫描的元素，所以i不能++)

优化：用随机的方式选择key（在《算法导论》中有数学证明，利用概率求期望）

class Solution {
public://获取随机数int getRandom(vector<int>&nums,int left,int right){int r_val=rand();return nums[r_val%(right-left+1)+left];}//快排void qsort(vector<int>&nums,int l,int r){if(l>=r) return ;//数组分区int key=getRandom(nums,l,r);int i=l,left=l-1,right=r+1;while(i<right){if(nums[i]<key) swap(nums[++left],nums[i++]);else if(nums[i]==key) i++;else if(nums[i]>key) swap(nums[--right],nums[i]);}//分成了[l,left][left+1,right-1][right,r-1]qsort(nums,l,left);qsort(nums,right,r);}//主体函数vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//种下随机数种子qsort(nums,0,nums.size()-1);return nums;    }
};

3、数组中第K个最大的元素

这道题就是之前数据结构堆中Top-K问题数据结构学习之堆-CSDN博客

而本期内容我们将介绍它的另外一种算法解决：快速选择算法

算法思想：数组分三块+随机选择基准元素

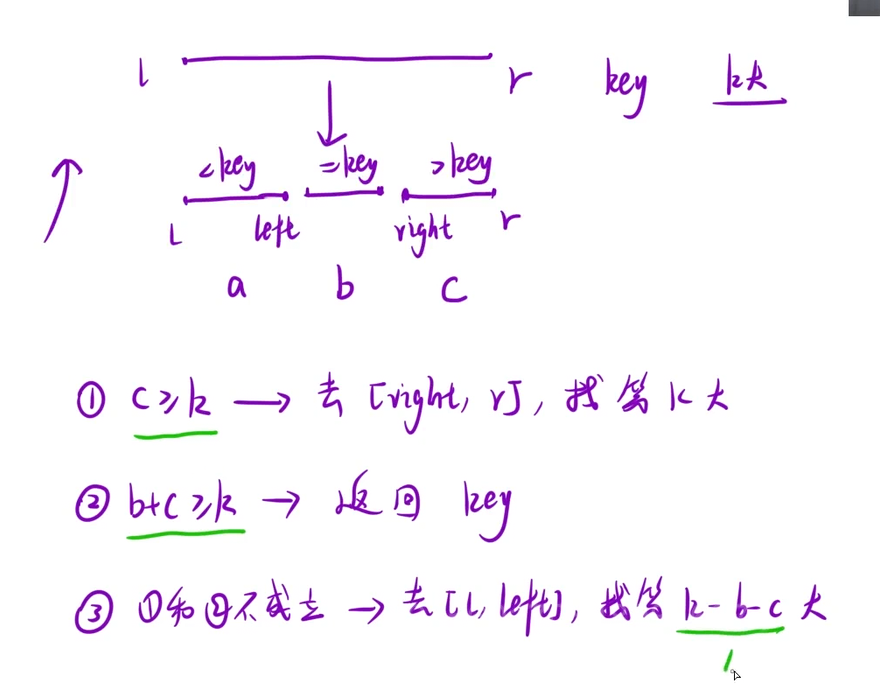
class Solution {
public://主题函数int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort(nums,0,nums.size()-1,k);}//快排int qsort(vector<int>&nums ,int l,int r,int k){if(l==r) return nums[l];//随机选择基准元素int key=getRandom(nums,1,r);//根据基本元素划分int i=l,left=l-1,right=r+1;while(i<right){if(nums[i]<key) swap(nums[++left],nums[i++]);else if(nums[i]==key) i++;else if(nums[i]>key) swap(nums[--right],nums[i]);}//分情况讨论int c=r-right+1,b=right-left-1;if(c>=k) return qsort(nums,right,r,k);else if(b+c>=k) return key;else return qsort(nums,l,left,k-b-c);}//获取随机数int getRandom(vector<int>&nums,int left,int right){int r_val=rand();return nums[r_val%(right-left+1)+left];}};

4、最小的K个数字

算法思想：有三种算法思想：排序、堆、快速选择

本篇重点讲解快速选择算法思想

算法一：排序

算法思路

将数组全部排序
取排序后数组的前k个元素

时间复杂度

O(n log n)：主要来自排序操作

class Solution {
public:vector<int> getLeastNumbers_Sort(vector<int>& arr, int k) {sort(arr.begin(), arr.end());return vector<int>(arr.begin(), arr.begin() + k);}
};

算法二：堆

算法思路

使用最大堆维护当前最小的k个元素
遍历数组，当堆大小小于k时直接加入
当堆已满时，如果当前元素小于堆顶，则替换堆顶元素
最终堆中元素即为最小的k个数字

时间复杂度

O(n log k)：每个元素最多需要一次堆操作

class Solution {
public:vector<int> getLeastNumbers_Heap(vector<int>& arr, int k) {if (k == 0) return vector<int>();priority_queue<int> maxHeap; // 最大堆for (int num : arr) {if (maxHeap.size() < k) {maxHeap.push(num);} else if (num < maxHeap.top()) {maxHeap.pop();maxHeap.push(num);}}vector<int> result;while (!maxHeap.empty()) {result.push_back(maxHeap.top());maxHeap.pop();}return result;}
};

算法三：快速选择

随机算法基准值+数组分三块

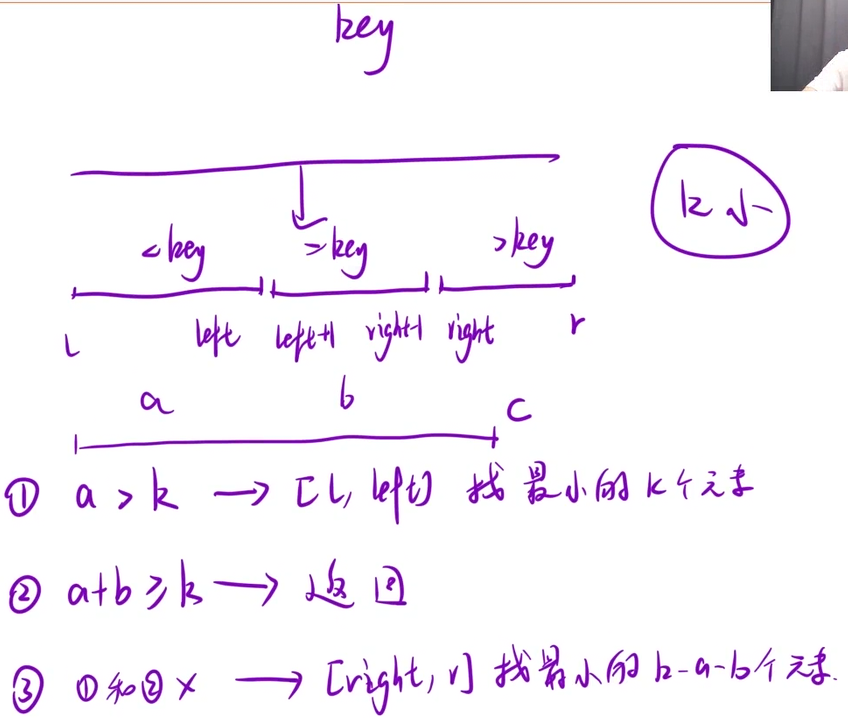
class Solution
{
public:vector<int> getLeastNumbers_Sort(vector<int>& arr, int k) {//快速选择算法srand(time(NULL));qsort(arr,0,arr.size()-1,k);return {arr.begin(),arr.begin()+k};}void qsort(vector<int>& arr, int l, int r, int k){if (l >= r) return;//随机选择基准值int key = getRandom(arr, l, r);//数组分三块int i = l, left = l - 1, right = r + 1;while (i < right){if (arr[i] < key) swap(arr[++left], arr[i++]);else if (arr[i] == key) i++;else if (arr[i] > key) swap(arr[--right], arr[i]);}//[l, left][left+1, right-1][right, r]int a=left-l+1,b=right-left,c=r-right+1;if(a>key) qsort(arr, l, left, k);else if(a+b>=key) qsort(arr, left+1, right-1, k-a);else qsort(arr, right, r, k-a-b);}int getRandom(vector<int>& arr, int l, int r){return arr[rand() % (r - l + 1) + l];}
};

5、排序数组（归并排序）

算法原理：合并两个有序数组

快排类似于二叉树的前序遍历过程，归并排序类似于二叉树的后序遍历过程

//优化前的版本：
//每次都要创建vector，开销比较大
class Solution {
public:void mergeSort(vector<int>nums, int left, int right){if (left >= right) return;//选择中间点划分区间int mid = left + (right-left) / 2;//递归排序左半区间mergeSort(nums, left, mid);//递归排序右半区间mergeSort(nums, mid + 1, right);//合并两个有序数组int cur1 = left,cur2 = mid + 1,i=0;vector<int>temp(right - left + 1);while (cur1 <= mid && cur2 <= right)temp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];//处理没有循环的情况，且只进去一个循环while (cur1 <= mid) temp[i++] = nums[cur1++];while (cur2 <= right) temp[i++] = nums[cur2++];//将temp数组中的元素复制到nums数组中}for (int i = left; i <= right; i++){nums[i] = temp[i-left];}}//主题函数vector<int> sortArray(vector<int>& nums){mergeSort(nums, 0, nums.size() - 1);return nums;}
};
//优化后的版本：
//递归中频繁创建空间的话最好将对应部分放到全局变量中
class Solution {
public:vector<int>temp;void mergeSort(vector<int>nums, int left, int right){if (left >= right) return;//选择中间点划分区间int mid = left + (right - left) / 2;//递归排序左半区间mergeSort(nums, left, mid);//递归排序右半区间mergeSort(nums, mid + 1, right);//合并两个有序数组int cur1 = left, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= right)temp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];//处理没有循环的情况，且只进去一个循环while (cur1 <= mid) temp[i++] = nums[cur1++];while (cur2 <= right) temp[i++] = nums[cur2++];//将temp数组中的元素复制到nums数组中}for (int i = left; i <= right; i++){nums[i] = temp[i - left];}}//主题函数vector<int> sortArray(vector<int>& nums){temp.resize(nums.size());mergeSort(nums, 0, nums.size() - 1);return nums;}
};

6、数组中的逆序对

算法思想：

策略1、找出该数之前有多少个数比我大（升序）

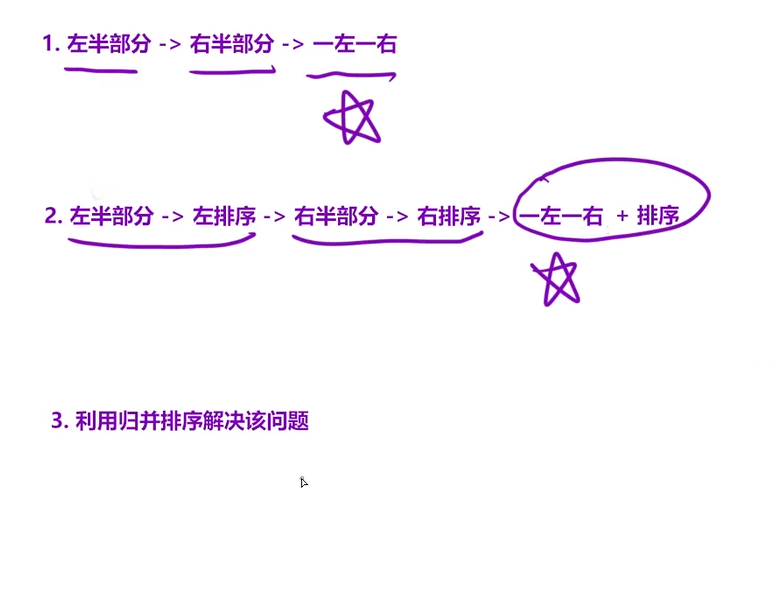
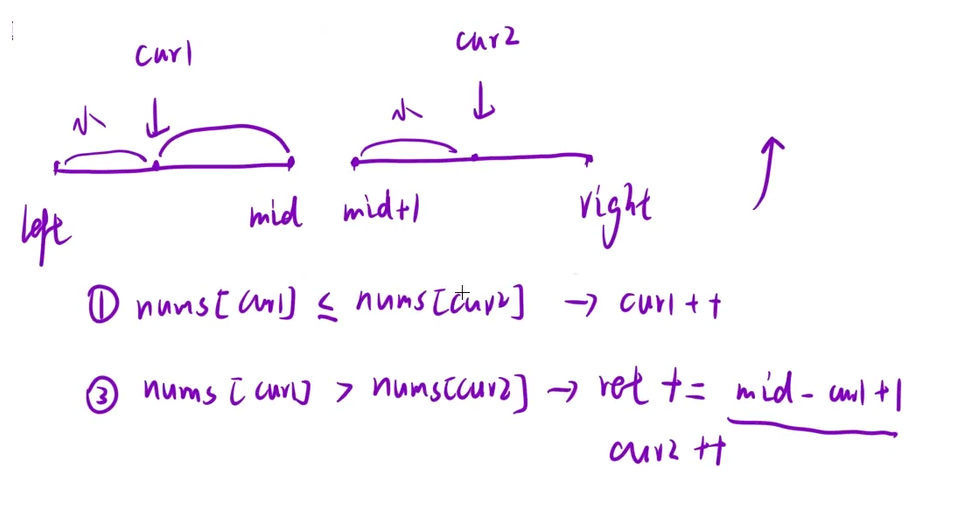
策略2、找出该数之后有多少个数比我小（降序）

class Solution {
public:int tmp[50010];//策略1：升序版本int reversePairs(vector<int>& nums){return mergeSort(nums, 0, nums.size() - 1);}int mergeSort(vector<int>& nums,int left,int right){if (left >= right) return;int ret = 0;//找中间位置分为两部分int mid = (right-left) / 2+left;//[left,mid][mid+1,right]//左边个数+排序+右边个数ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);//一左一右个数int cur1 = left, cur2 = mid + 1,i=0;while (cur1 <= mid && cur2 <= right){if (nums[cur1] <= nums[cur2]){tmp[i++] = nums[cur1++];}else//统计个数{ret+=mid-cur1+1;tmp[i++] = nums[cur2++];}}//处理边界情况while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= right) tmp[i++] = nums[cur2++];for (int j = left; j <= right; j++){nums[j] = tmp[j - left];}return ret;}};
class Solution
{public:int tmp[50010];//策略2：降序版本int reversePairs(vector<int>& nums){return mergeSort(nums, 0, nums.size() - 1);}int mergeSort(vector<int>& nums, int left, int right){if (left >= right) return;int ret = 0;//找中间位置分为两部分int mid = (right - left) / 2 + left;//[left,mid][mid+1,right]//左边个数+排序+右边个数ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);//一左一右个数int cur1 = left, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= right){if (nums[cur1] <= nums[cur2]){tmp[i++] = nums[cur2++];}else//统计个数{ret += mid - cur2 + 1;tmp[i++] = nums[cur1++];}}//处理边界情况while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= right) tmp[i++] = nums[cur2++];for (int j = left; j <= right; j++){nums[j] = tmp[j - left];}return ret;}
};

7、计算右侧小于当前元素的个数

算法思想：找出该数之后有多少个数比我小（降序）

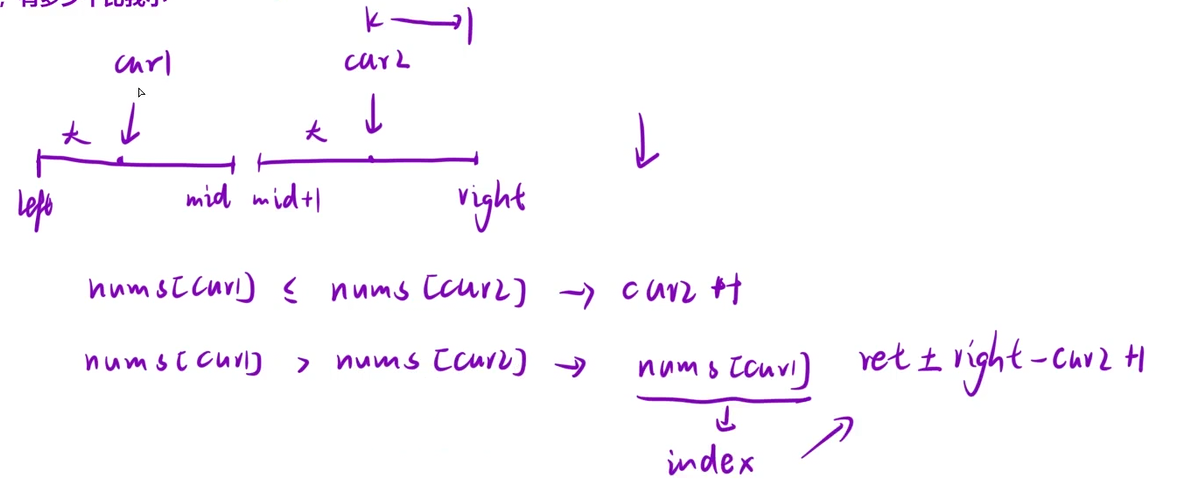
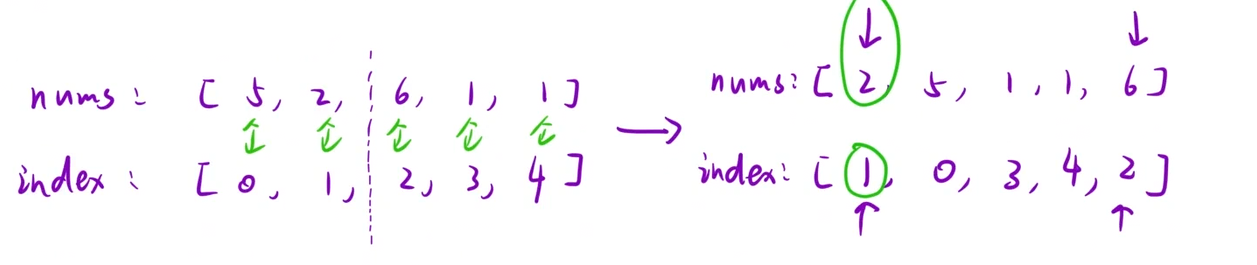
细节问题：nums原始下标是多少？

class Solution {
public:vector<int>ret;vector<int>index;//记录nums中原始下标int tmpNums[5000010];int tmpindex[5000010];vector<int> countSmaller(vector<int>& nums) {int n=nums.size();ret.resize(n);index.resize(n);//初始化indexfor(int i=0;i<n;i++){index[i]=i;}mergesort(nums,0,n-1);    return ret;}void mergesort(vector<int>&nums,int left,int right){if(left>=right) return;//根据中间位置划分元素int mid=left+(right-left)/2;//[left,mid][mid+1,right]mergesort(nums,left,mid);mergesort(nums,mid+1,right);//一左一右个数int cur1 = left, cur2 = mid + 1,i=0;while (cur1 <= mid && cur2 <= right)//降序{if (nums[cur1] <= nums[cur2]){tmpNums[i] = nums[cur2];tmpindex[i++]=index[cur2++];}else{ret[index[cur1]]+=right-cur2+1;//重点tmpNums[i]=nums[cur1];tmpindex[i++]=index[cur1++];}}//处理边界情况while (cur1 <= mid) {tmpNums[i]=nums[cur1];tmpindex[i++]=index[cur1++];}while (cur2 <= right) {tmpNums[i]=nums[cur2];tmpindex[i++]=index[cur2++];}//还原for(int j=left;j<=right;j++){nums[j]=tmpNums[j-left];index[j]=tmpindex[j-left];}}
};

8、翻转对

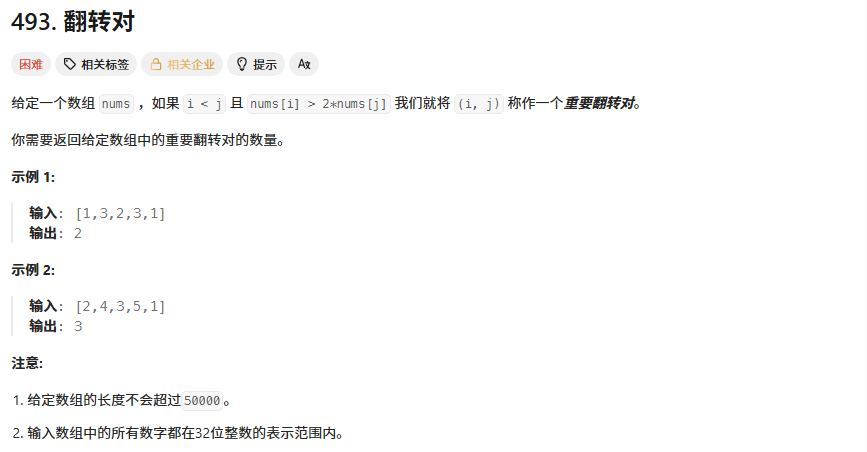
算法思路：类似于前面的逆序对

计算翻转对

class Solution {
public:int tmp[50010];int reversePairs(vector<int>& nums){return mergeSort(nums, 0, nums.size() - 1);}int mergeSort(vector<int>& nums, int left, int right){if(left >= right) return 0;int ret = 0;// 1. 先根据中间元素划分区间int mid = (left + right) >> 1;// [left, mid] [mid + 1, right]// 2. 先计算左右两侧的翻转对ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);// 3. 先计算翻转对的数量int cur1 = left, cur2 = mid + 1, i = left;while(cur1 <= mid) // 降序的情况{while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0) cur2++;if(cur2 > right)break;ret += right - cur2 + 1;cur1++;}// 4. 合并两个有序数组cur1 = left, cur2 = mid + 1;while(cur1 <= mid && cur2 <= right)tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur2++] : nums[cur1++];while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; j++)nums[j] = tmp[j];return ret;}
};

本期内容就到这里，喜欢请点个赞谢谢