当前位置：首页 > news >正文

25高教社杯数模国赛【C题国一学长思路+问题分析】

news 2025/9/5 8:06:13

注：本内容由”数模加油站“ 原创出品，虽无偿分享，但创作不易。
欢迎参考teach，但请勿抄袭、盗卖或商用。

C 题 NIPT的时点选择与胎儿的异常判定

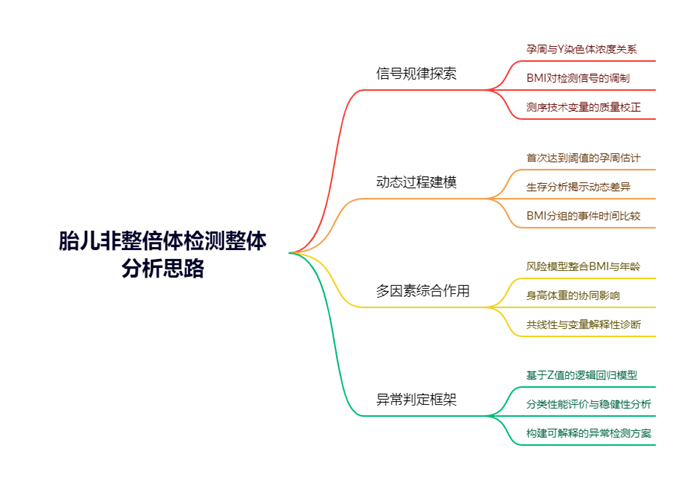
本题以胎儿非整倍体检测为研究对象，结合孕妇临床信息、测序质量指标以及染色体信号数据，要求在不同角度下建立数据驱动的分析框架。整体思路的核心在于，通过系统化的数据清洗、变量构建与统计建模，将复杂的检测数据转化为具有解释性的判定依据，并逐步形成完整的分析链条。

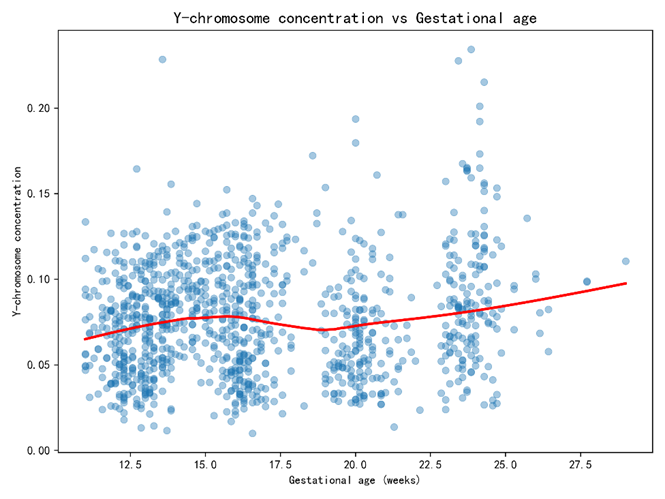
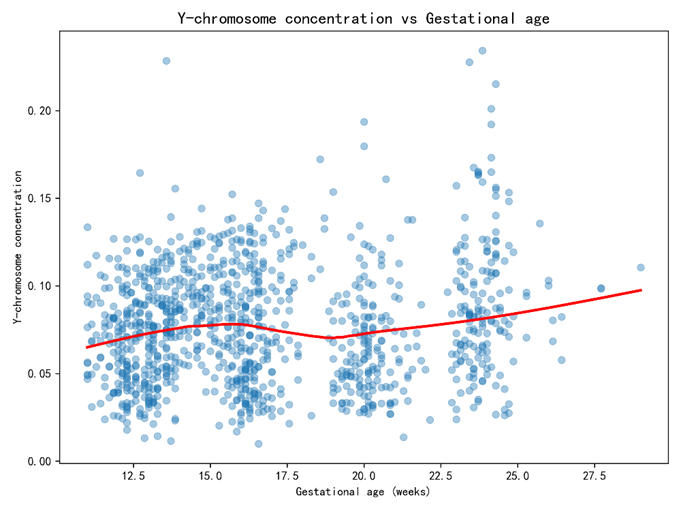
在第一问中，重点放在信号生成机制的探索。通过孕周、BMI 与 Y 染色体浓度的关联分析，识别孕期进程与个体特征对检测信号的影响，并结合测序技术变量进行质量校正，从而建立起信号稳定性与可解释性的初步框架。
第二问进一步引入动态过程，关注 Y 染色体浓度首次达到稳定阈值的孕周。通过生存分析与分组比较，揭示 BMI 等体格因素在信号累积过程中的差异，形成以“时间—事件”为主线的动态描述，为临床检测时机的优化提供依据。
第三问在此基础上引入多元因素，采用风险模型刻画 BMI、年龄、身高、体重等变量的综合作用。通过多因素协同分析，不仅考察单一变量的边际效应，更揭示潜在的交互与共线性影响，增强了对检测结果变异性的整体解释力。
第四问以异常判定为核心，直接利用染色体 Z 值及相关指标建立逻辑回归框架，将前期对信号、动态与风险因素的探索汇聚到分类判定之中。通过模型估计与性能评价，形成一套可解释且稳健的异常检测方案。
体来看，四个问题由浅入深、逐步递进，从单一信号的规律挖掘，到动态过程的建模，再到多因素综合作用的刻画，最终落实到分类与判定的任务。该过程既保证了统计学的严谨性与逻辑性，也兼顾了模型的透明性与可解释性，为生物医学背景下的实际应用提供了系统化的解决思路。
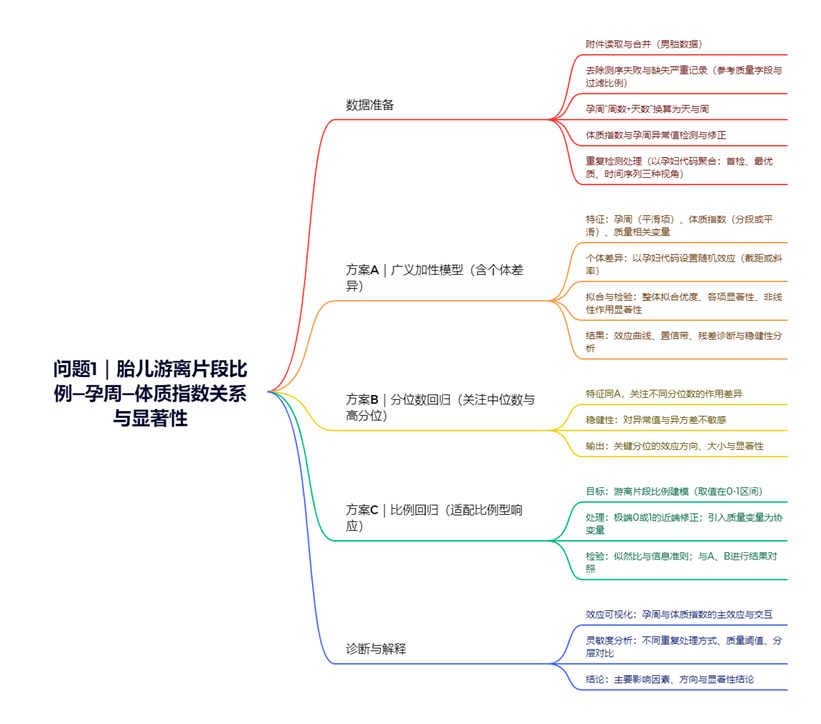
在这里插入图片描述
问题1

在这里插入图片描述
问题 1 分析
1）思路框架｜以“男胎 Y 染色体浓度”为核心的关系刻画与证据链构建
（数据分析与挖掘为主）

在本题场景中，每位受试者可能存在多次检测记录（字段“孕妇代码”“检测抽血次数”“检测日期”），且关键响应指标为“Y染色体浓度”，协变量涵盖妊娠进程（“检测孕周”以“w+”形式给出）、体格状态（“孕妇BMI”）以及多项测序质量与技术特征（如“原始读段数”“在参考基因组上比对的比例”“重复读段的比例”“唯一比对的读段数”“GC含量”“被过滤掉读段数的比例”等）。为保证统计推断的严谨性与可解释性，首先统一数据口径与时间结构：将“检测孕周”的字符串型记法解析为连续周数，若“检测孕周”为“ $w$ w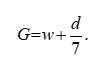+ $d$ ”，则定义在这里插入图片描述
对极少数仅有“ $w$ w”的记录，取 $d = 0$ 。与此同时，将“检测日期”转为标准日期类型以校验时间先后与重复记录的合理性，确保同一“孕妇代码”内的观测按时间有序。

为保证比例类响应的稳健性，先对“Y染色体浓度”进行近端修正与标准化处理。记原始比例为 $p∈[0,1]p\in[0,1]$ ，设微小常数 $ε\varepsilon$ （如 $ε=10−4\varepsilon=10^{-4}$ ），定义
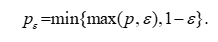
在这里插入图片描述
随后对妊娠进程与体格状态建立统一度量体系：若需复核“孕妇BMI”的一致性，可用身高（厘米）与体重（千克）计算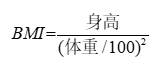
并与“孕妇BMI”字段做一致性检查；分析中以“孕妇BMI”为准，异常差值视为数据质量线索。对时间相关的多次检测，采用“以孕妇为单位”的纵向结构组织数据，并在模型层面使用以“孕妇代码”为聚类单位的稳健方差估计，既避免复杂层级结构增加解释负担，又能控制同一受试者内相关性带来的显著性偏差。

质量控制与异常识别方面，先对关键技术变量的取值域进行经验核验与分布检视，例如“在参考基因组上比对的比例”与“重复读段的比例”应处于合理区间，对“被过滤掉读段数的比例”与“原始读段数”联合绘制散点与分位图，辨识低读段高过滤的可疑组合。对“GC含量”“13/18/21号染色体的GC含量”进行密度与箱线分析，识别极端 GC 偏倚记录；若发现技术变量的极端取值对 $pεp_\varepsilon$ 产生系统性影响，则在后续建模中以协变量控制其混杂效应。对同一“孕妇代码”的多次检测，检查与 $pεp_\varepsilon$ 的时间轨迹，若出现非生物学合理的剧烈跳变（例如短期内 $pεp_\varepsilon$ 大幅下降且伴随质量指标显著异常），则标注为高影响点候选，在拟合后进行影响度诊断与灵敏度分析。

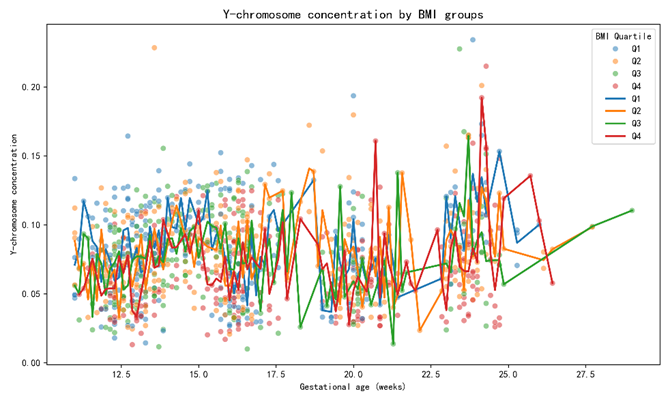
在探索性分析阶段，围绕“妊娠进程—体格状态—技术质量”三条主线构造证据链：其一，考察 $pεp_\varepsilon$ 随 $G$ 的单调性与曲率（散点图与局部平滑），为线性或弱非线性关系提供直观依据；其二，分层绘制不同 BMI 区间（如按四分位划分）的 $pεp_\varepsilon$ – $G$ 关系，以辨识“孕周×体格”交互的必要性；其三，评估质量变量（如“在参考基因组上比对的比例”“重复读段的比例”“被过滤掉读段数的比例”“原始读段数”“唯一比对的读段数”“GC含量”）与 $pεp_\varepsilon$ 的相关方向，确认哪些应作为控制项进入模型以剥离技术层面的系统偏差。最终形成：以 $pεp_\varepsilon$ 为核心响应，以 $G$ 与 $BM I$ 为主要解释，以若干质量指标为控制变量的关系刻画框架，并在“孕妇代码”聚类层面进行稳健推断，使本题的统计证据与后续“首次达标时间”的决策口径保持一致。

解题思路：
2）数学模型构建｜分数响应的对数几率回归（基础可解释框架）

为直接刻画“Y染色体浓度”的比例属性，引入对数几率变换
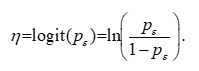
在这里插入图片描述
在不牺牲可解释性的前提下，采用广义线性模型的二项族链接形式（分数响应的对数几率回归，使用准似然解释），设样本量为 $n$ ，第 $i$ 条观测对应的线性预测子为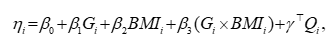
其中 $Q_i$ 为技术质量控制向量，可包含“在参考基因组上比对的比例”“重复读段的比例”“唯一比对的读段数”“原始读段数”“GC含量”“被过滤掉读段数的比例”等经前述检视后保留的变量。模型的均值—链接关系为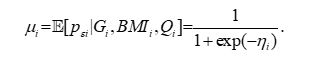在这里插入图片描述
若探索性分析显示 $pεp_\varepsilon$ 对 $G$ 的关系存在轻微曲率，可在不改变模型范式的前提下加入二次项并以嵌套方式检验其必要性：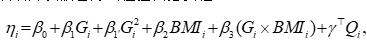
但仅当诊断证据充分时才保留 $G_i^2$ ，以维持本题“基础统计模型、强解释性”的要求。为处理同一受试者的多次观测，对参数显著性与区间估计采用以“孕妇代码”为聚类单位的稳健方差估计，记聚类索引为 $c=1,…,Cc=1,\dots,C$ ，则三明治估计量的结构为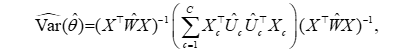在这里插入图片描述
其中 $θ=(β0,β1,β2,β3,γ⊤)⊤\theta=(\beta_0,\beta_1,\beta_2,\beta_3,\gamma^\top)^\top$ ， $X$ 为设计矩阵， $W^\widehat W$ 来自链接下的权重矩阵， $U^c\widehat U_c$ 为第 $c$ 个聚类的得分残差。

该模型的解释路径清晰： $G$ 的边际效应通过 $β1\beta_1$ （以及必要时的 $β1′\beta_1'$ ）量化“孕周推进”对对数几率的影响； $BM I$ 的边际效应通过 $β2\beta_2$ 刻画“体格状态”对浓度比例的独立作用； $β3\beta_3$ 则描述“孕周×BMI”的交互调制； $γ\gamma$ 聚合地剥离技术层面系统偏差，保证生物学关系的纯化估计。这一设置与后续围绕“首次达标时间”的决策框架在变量口径与控制思路上完全一致。

3）模型算法求解｜极大（准）似然、迭代加权最小二乘与聚类稳健推断在对数几率链接下，记第 $i$ 条观测的均值为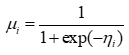在这里插入图片描述
将 $pεip_{\varepsilon i}$ 视作分数响应的准似然目标，其对数（准）似然可写为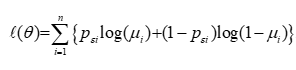
求解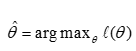
可采用牛顿—拉夫森或迭代加权最小二乘（IRLS）算法。记第 $t$ 次迭代的工作响应与权重为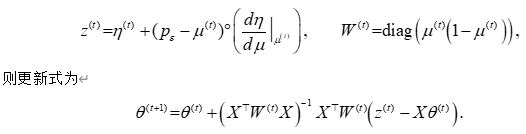
算法收敛后，基于聚类稳健三明治估计获得参数标准误与置信区间；对线性假设（如 $β3=0\beta_3=0$ 、或 $β1′=0\beta_1'=0$ ）使用稳健沃尔德检验或稳健得分检验评估交互与非线性项的必要性。诊断环节包括：（i）工作残差与杠杆值联合识别高影响点，若高影响点集中于特定质量阈值之外，则以“技术质量”为线索进行灵敏度剔除；（ii）对 $G$ 的函数型进行局部平滑对照，若对照显示显著曲率，再以嵌套方式引入 $G^2$ 并复核其稳健性；（iii）对“孕妇代码”层面的组内相关进行事后检验，确认聚类稳健结论的稳定。
在实现层面，按照“先统一口径—再建模—后诊断—必要时最小幅度修正”的顺序执行，保证模型仅作为“对探索性证据的参数化表达”，避免在缺乏量化结果的情形下进行模型间比较。最终输出的将是围绕 $pεp_\varepsilon$ 、 $G$ 、 $BM I$ 与质量控制变量之间关系的参数化刻画与显著性证据，其变量定义、时间口径与控制思路与后续题目的“首次达标时间”与“代价最小化的单点决策”天然对齐。
在这里插入图片描述

Python代码：

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as snsimport matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体（如黑体）
matplotlib.rcParams['axes.unicode_minus'] = False    # 正常显示负号
# -------------------------------
# Create result folder
# -------------------------------
os.makedirs("result1", exist_ok=True)
# -------------------------------
# Load male dataset (Q1 focuses on Y-conc vs gestational age & BMI)
# -------------------------------
male_df = pd.read_csv("附件_男胎检测数据.csv", encoding="utf-8")# -------------------------------
# Parse gestational age (format: "Xw+Y" or "Xw")
# -------------------------------
def parse_gestational_age(s):try:s = str(s)if "w+" in s:w, d = s.replace("w", "").split("+")return int(w) + int(d)/7elif "w" in s:w = s.replace("w","")return int(w)else:return np.nanexcept:return np.nanmale_df["Gestational_age"] = male_df["检测孕周"].astype(str).map(parse_gestational_age)
male_df["Y_conc"] = pd.to_numeric(male_df["Y染色体浓度"], errors="coerce").clip(0,1)
male_df["BMI"] = pd.to_numeric(male_df["孕妇BMI"], errors="coerce")# -------------------------------
# Keep only valid rows
# -------------------------------
df = male_df.dropna(subset=["Gestational_age","Y_conc","BMI"])# -------------------------------
# Scatter plot with regression line
# -------------------------------
plt.figure(figsize=(8,6))
sns.scatterplot(data=df, x="Gestational_age", y="Y_conc", alpha=0.4, edgecolor=None)
sns.regplot(data=df, x="Gestational_age", y="Y_conc", scatter=False, color="red", lowess=True)
plt.title("Y-chromosome concentration vs Gestational age", 
fontsize=14)
plt.xlabel("Gestational age (weeks)")
plt.ylabel("Y-chromosome concentration")
plt.tight_layout()
plt.savefig("result1/yconc_vs_gestational.png", dpi=300)
plt.close()# -------------------------------
# Stratify by BMI quartiles
# -------------------------------
df["BMI_group"] = pd.qcut(df["BMI"], 4, labels=["Q1","Q2","Q3","Q4"])plt.figure(figsize=(10,6))
sns.scatterplot(data=df, x="Gestational_age", y="Y_conc", hue="BMI_group", alpha=0.5)
sns.lineplot(data=df, x="Gestational_age", y="Y_conc", hue="BMI_group", estimator="mean", ci=None, linewidth=2)
plt.title("Y-chromosome concentration by BMI groups", fontsize=14)
plt.xlabel("Gestational age (weeks)")
plt.ylabel("Y-chromosome concentration")
plt.legend(title="BMI Quartile")
plt.tight_layout()
plt.savefig("result1/yconc_by_bmi.png", dpi=300)
plt.close()# -------------------------------
# Correlation heatmap for technical variables
# -------------------------------
tech_vars = ["在参考基因组上比对的比例","重复读段的比例","唯一比对的读段数","原始读段数","GC含量","被过滤掉读段数的比例"]
df.columns = df.columns.str.strip()
tech_df = df[tech_vars + ["Y_conc"]].apply(pd.to_numeric, errors="coerce")
corr = tech_df.corr()plt.figure(figsize=(8,6))
sns.heatmap(corr, annot=True, fmt=".2f", cmap="coolwarm", cbar=True)
plt.title("Correlation heatmap (Y-conc & technical variables)", fontsize=14)
plt.tight_layout()
plt.savefig("result1/heatmap_corr.png", dpi=300)
plt.close()
# -------------------------------
# Save correlation summary table
# -------------------------------
corr_with_y = corr["Y_conc"].sort_values(ascending=False)
summary_table = corr_with_y.to_frame("Correlation_with_Yconc")
summary_table.to_csv("result1/correlation_summary.csv")print("All plots and summary table have been saved in the 'result1' folder.")