C语言习题整理①
一些C语言习题的整理。
目录
一、判断质数
二、判断回文数
三、判断水仙花数
四、输出乘法表
五、输出杨辉三角
一、判断质数
质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数(规定1既不是质数也不是合数)。质数的个数是无穷的。
这道题思路不难,令用户输入数字num,设置一个cnt用来计数,在循环中令i从2开始递增,如果num对i模为0证明可以被整除,则cnt++,如果cnt最终仍旧为0说明没有数可以整除它,该数字就是质数。
代码实现:
#include<stdio.h>
int main(void)
{
int cnt,num;
int i;
printf("plz enter the number, enter q to quit:\n");
while(scanf("%0d",&num) != 0)
{
cnt = 0;
for(i=2;i<num;i++)
{
if(num%i == 0)
cnt++;
}
if(cnt)
printf("%0d is not prime number.\n",num);
else
printf("%0d is prime number.\n",num);
printf("plz enter next number, enter q to quit:\n");
}
return 0;
}运行结果:
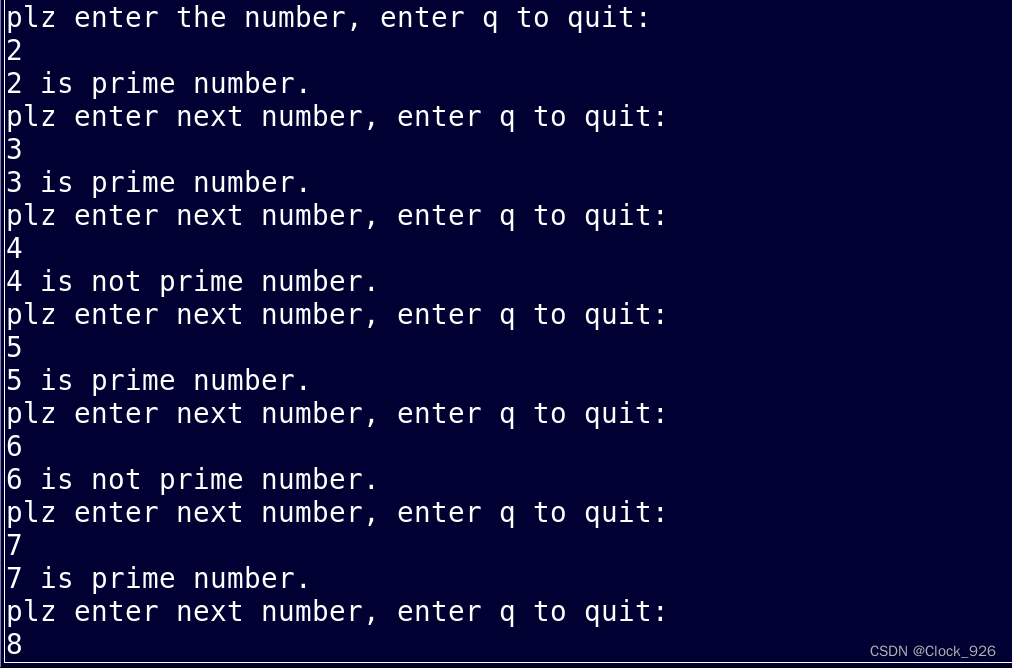
也可以变化一下,直接显示输入数字内含有的所有质数:
#include<stdio.h>
int main(void)
{
int cnt,num;
int i,j;
printf("plz enter the number, enter q to quit:\n");
while(scanf("%0d",&num) != 0)
{
printf("num is %0d.\n",num);
for(i=2;i<=num;i++)
{
cnt = 0;
for(j=2;j<i;j++)
{
if(i%j == 0)
cnt++;
}
if(!cnt)
printf("%0d is prime number.\n",i);
}
printf("plz enter next number, enter q to quit:\n");
}
return 0;
}运行结果:
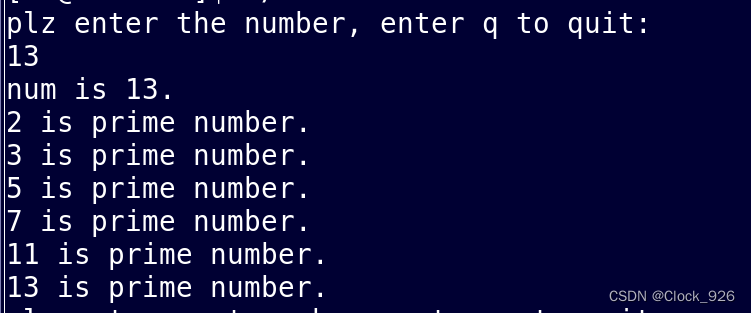
二、判断回文数
回文数就是正向排列和反向排列是一样的数字。设n是一任意自然数,若将n的各位数字反向排列所得自然数n1与n相等,则称n为一回文数。例如,若n=1234321,那么n就是回文数。
首先回文数必须要大于100,否则没有意义。对于1000以内的数字,可以通过判断数字的百位数和个位数是否相等,从而列出所有的回文数。代码实现:
int main(void)
{
int num;
int a,b,c,i;
printf("plz enter the number, q to quit:\n");
while(scanf("%0d",&num) != 0)
{
printf("answer is:\n");
for(i=100;i<=num;i++)
{
c = i%10;
b = (i/10)%10;
a = i/100;
if(a == c)
printf("%5d",i);
}
printf("\n");
printf("plz enter next number, q to quit:\n");
}
return 0;
}运行结果:

这种方法比较简单直接,但是有很大局限性。可以使用另外一种更加灵活的通用方法,将数字当作字符串来看待,通过反转赋值来实现判断。代码实现:
#include<stdio.h>
#include<string.h>
int main(void)
{
char str[999];
char str_reverse[999];
int i,j;
printf("plz enter:\n");
gets(str);
int n = strlen(str);
printf("cotent is: %s\n", str);
str_reverse[n] = '\0';
for (i=0,j=n-1;i<n;i++,j--)
{
str_reverse[j] = str[i];
}
printf("reverse content is: %s\n", str_reverse);
if(strcmp(str_reverse, str) == 0)
printf("%s is palindrome.\n", str);
else
printf("%s is not palindrome.\n", str);
return 0;
}运行结果:
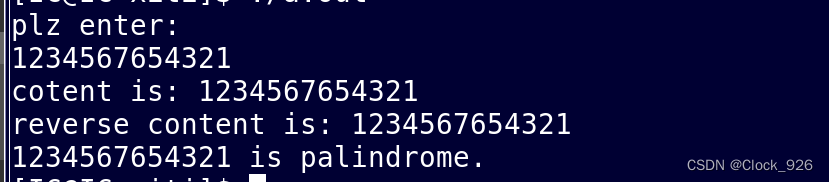
三、判断水仙花数
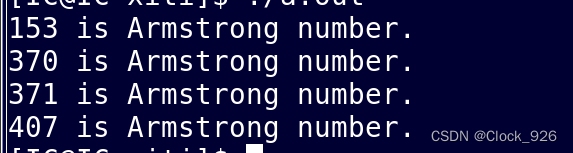
水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number),水仙花数是指一个 3 位数,它的每个数位上的数字的 3次幂之和等于它本身。例如:1^3 + 5^3+ 3^3 = 153。
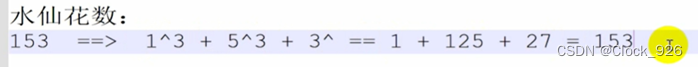
水仙花数只是自幂数的一种,严格来说3位数的3次幂数才称为水仙花数。
其他位数的自幂数名字:
- 一位自幂数:独身数
- 三位自幂数:水仙花数
- 四位自幂数:四叶玫瑰数
- 五位自幂数:五角星数
- 六位自幂数:六合数
- 七位自幂数:北斗七星数
- 八位自幂数:八仙数
- 九位自幂数:九九重阳数
- 十位自幂数:十全十美数
这个逻辑就非常简单了,只需要简单的判断加和即可。代码实现:
#include<stdio.h>
#include<math.h>
int main(void)
{
int a,b,c;
int num;
for(num=100;num<1000;num++)
{
c = num%10;
b = (num/10)%10;
a = num/100;
if(num == pow(a,3)+pow(b,3)+pow(c,3))
printf("%0d is Armstrong number.\n",num);
}
return 0;
}运行结果:
四、输出乘法表
依次输出乘法表,是一道比较基础的题,嵌套循环即可。参数可任意更改。
代码实现:
#include<stdio.h>
#define row 9
#define col 9
int main(void)
{
int i,j;
for(i=1;i<=row;i++)
{
for(j=1;j<=i;j++)
{
printf("%5d",i*j);
}
printf("\n");
}
return 0;
}运行结果:

五、输出杨辉三角
杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一。杨辉三角把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。
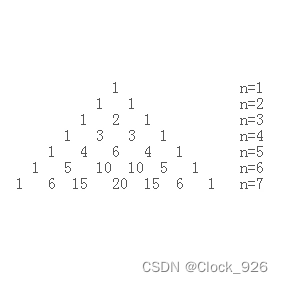
杨辉三角的特性:
- 每个数等于它上方两数之和。
- 每行数字左右对称,由1开始逐渐变大。
- 第n行的数字有n项。
- 前n行共[(1+n)n]/2 个数。
- 第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
- 第n行的第m个数和第n-m+1个数相等 ,为组合数性质之一。
- 每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
- (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
- 将第2n+1行第1个数,跟第2n+2行第3个数、第2n+3行第5个数……连成一线,这些数的和是第4n+1个斐波那契数;将第2n行第2个数(n>1),跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
- 将第n行的数字分别乘以10^(m-1),其中m为该数所在的列,再将各项相加的和为11^(n-1)。例如有,11^0=1,11^1=1x10^0+1×10^1=11,11^2=1×10^0+2x10^1+1x10^2=121,11^3=1x10^0+3×10^1+3x10^2+1x10^3=1331,11^4=1x10^0+4x10^1+6x10^2+4x10^3+1x10^4=14641,11^5=1x10^0+5x10^1+10x10^2+10x10^3+5x10^4+1×10^5=161051。
- 第n行数字的和为2^(n-1)。1=2^(1-1),1+1=2^(2-1),1+2+1=2^(3-1),1+3+3+1=2^(4-1),1+4+6+4+1=2^(5-1),1+5+10+10+5+1=2^(6-1)。
- 斜线上数字的和等于其向左(从左上方到右下方的斜线)或向右拐弯(从右上方到左下方的斜线),拐角上的数字。1+1=2,1+1+1=3,1+1+1+1=4,1+2=3,1+2+3=6,1+2+3+4=10,1+3=4,1+3+6=10,1+4=5。
- 将各行数字左对齐,其右上到左下对角线数字的和等于斐波那契数列的数字。1,1,1+1=2,2+1=3,1+3+1=5,3+4+1=8,1+6+5+1=13,4+10+6+1=21,1+10+15+7+1=34,5+20+21+8+1=55。
对于实现过程,依旧需要使用嵌套循环,我们可以利用数组来进行操作,可以很方便地对每行的首尾赋值1。而每行的中间量是上一行值的和,最后控制打印空格和值。
代码实现:
#include<stdio.h>
int main(void)
{
int row,col,level;
printf("plz enter the level, press q to quit:\n");
while(scanf("%d",&level) != 0)
{
int arr[level][level];
for(row=0;row<level;row++)
{
arr[row][0] = 1;
arr[row][row] = 1;
}
for(row=2;row<level;row++)
{
for(col=1;col<=row-1;col++)
{
arr[row][col] = arr[row-1][col-1] + arr[row-1][col];
}
}
for(row=0;row<level;row++)
{
for(col=0;col<=level-row;col++)
{
printf(" ");
}
for(col=0;col<=row;col++)
{
printf("%5d",arr[row][col]);
}
printf("\n");
}
printf("\n");
printf("plz enter next level, press q to quit:\n");
}
return 0;
}根据传入的杨辉三角层级来创建二维数组。第一次循环,使得数组的头尾都为1。第二次循环,从这一行开始,数组值为上方的两数之和。第三次循环进行打印,根据排序依次打印空格和数字。
运行结果:
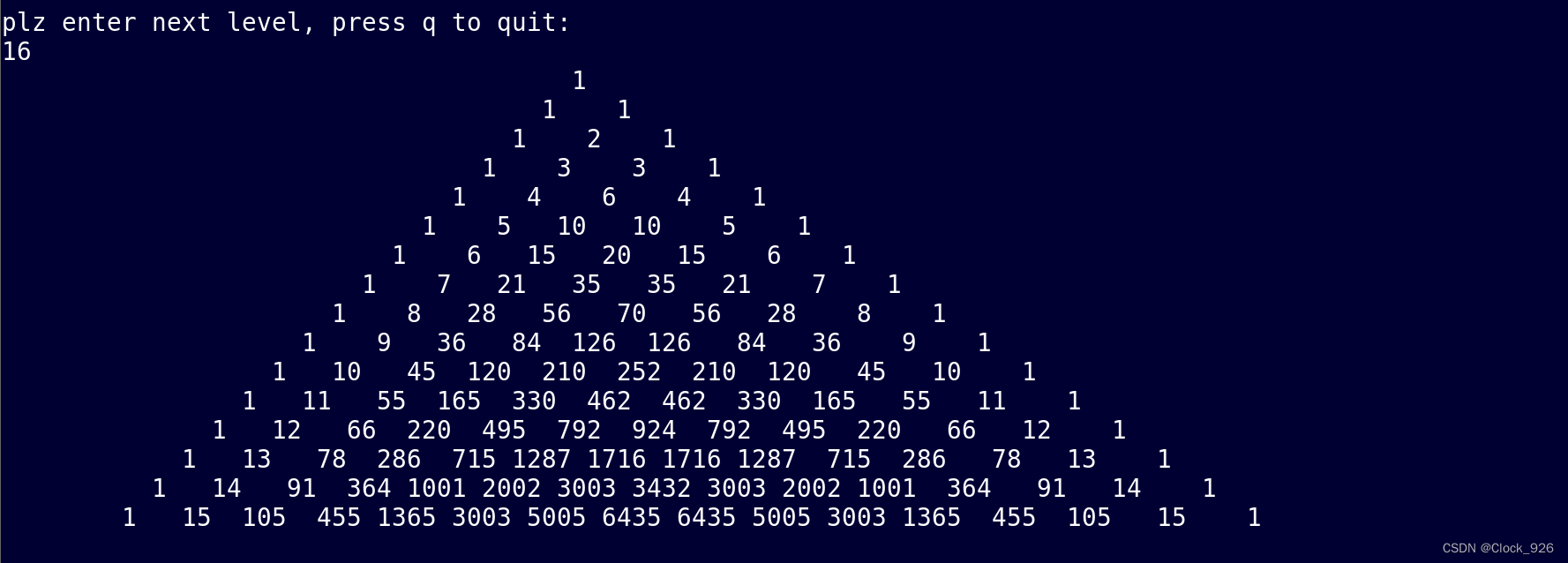
只要你的屏幕够大,还可以打印出更高层级的杨辉三角😀
