当前位置： 首页 > news >正文

吴恩达机器学习补充：决策树和随机森林

news 2025/9/2 8:00:18

数据集：通过网盘分享的文件：sonar-all-data.csv
链接: https://pan.baidu.com/s/1D3vbcnd6j424iAwssYzDeQ?pwd=12gr 提取码: 12gr

学习来源：https://github.com/cabin-w/MLBeginnerHub

定义

决策树的定义

决策树（Decision Tree）是一种基于树状结构进行决策的监督学习算法，其核心思想是通过对数据特征的逐步划分，模拟人类决策过程，最终实现对目标变量的预测（分类或回归）。

  • 结构组成：

    • 根节点：代表整个数据集，是决策树的起点。

    • 内部节点：每个内部节点对应一个特征，用于对数据进行划分（如 “年龄是否大于 30 岁”“收入是否高于 5 万元”）。

    • 分支：每个分支表示基于特征划分的结果（如 “是” 或 “否”）。

    • 叶节点：树的末端，代表最终的决策结果（如分类问题中的类别，回归问题中的数值）。

  • 工作原理： 从根节点开始，根据特征的重要性（如通过信息增益、基尼系数等指标衡量）选择最优特征，将数据划分为不同子集；对每个子集重复这一过程，直到子集中的样本属于同一类别（分类）或差异足够小（回归），形成叶节点。

  • 示例： 预测 “用户是否购买商品” 时，决策树可能先按 “年龄” 划分，再按 “是否有优惠券” 进一步划分，最终叶节点输出 “购买” 或 “不购买”。

随机森林的定义

随机森林（Random Forest）是一种集成学习算法，通过构建多个决策树并综合其结果来提高预测性能，减少过拟合风险。

  • 核心思想： 基于 “集成思想”—— 多个弱分类器（决策树）的组合可以形成强分类器。具体通过两个随机性实现：

    • 样本随机：从原始数据中通过bootstrap 抽样（有放回抽样）生成多个不同的训练子集，每个子集用于训练一棵决策树。

    • 特征随机：在每棵决策树的每个节点划分时，从所有特征中随机选择部分特征（如总特征数的平方根），仅基于这些特征进行最优划分。

    • 由以上两个随机，我们就可以发现单棵决策树决策树的问题在于结果不稳定。

  • 预测规则：

    • 分类问题：多数投票法（所有决策树的预测结果中，出现次数最多的类别为最终结果）。

    • 回归问题：平均值法（所有决策树的预测结果的平均值为最终结果）。

  • 优势： 相比单一决策树，随机森林泛化能力更强，对噪声数据更稳健，且不易过拟合。

总结

算法本质核心特点应用场景
决策树单一树状模型直观易懂，易过拟合简单分类 / 回归、规则提取
随机森林多棵决策树的集成性能更优，抗过拟合，稳定性高复杂数据预测、特征重要性评估

代码实现

加载数据

def loadCSV(filename):  # 定义loadCSV函数，参数为filenamedataSet = []  # 创建空列表dataSetwith open(filename, 'r') as file:  # 用只读方式打开filename文件并赋值给filecsvReader = csv.reader(file)  # 用csv模块的reader方法读取file文件并赋值给csvReader（分割处理）for line in csvReader:  # 遍历csvReader中的每一行dataSet.append(line)  # 将每一行添加到dataSet列表中return dataSet  # 返回dataSet列表

预处理

# 除了判别列，其他列都转换为float类型
def column_to_float(dataSet):  # 定义column_to_float函数，参数为dataSetfeatLen = len(dataSet[0]) - 1  # 获取dataSet中最后一列的索引for data in dataSet:  # 遍历dataSet中的每一行for column in range(featLen):  # 遍历每一行中除最后一列之外的每一列data[column] = float(data[column].strip())  # 将每一列的字符串转换为浮点数并赋值回原位置

将数据集分成N块，方便交叉验证

def spiltDataSet(dataSet, n_folds):fold_size = int(len(dataSet) / n_folds)  # 计算每份数据的大小dataSet_copy = list(dataSet)  # 复制数据集dataSet_spilt = []  # 创建用于存储分割后数据集的列表for i in range(n_folds):  # 循环n_folds次，将数据集分割成n份fold = []  # 创建一个空列表用于存储每份数据while len(fold) < fold_size:  # 当该份数据未达到应有的大小时index = randrange(len(dataSet_copy) - 1)  # 随机选择数据集中的索引（不放回）fold.append(dataSet_copy.pop(index))  # 将随机选择的数据加入该份数据，并从数据集中移除dataSet_spilt.append(fold)  # 将该份数据添加到分割后数据集列表中return dataSet_spilt  # 返回分割后的数据集列表

构造数据子集

# 从原始数据集中随机抽取指定比例的样本，构建一个数据子集，
#且采用的是有放回抽样（即同一个样本可能被多次选中）
def get_subsample(dataSet, ratio):subdataSet = []  # 创建空列表用于存储子样本lenSubdata = round(len(dataSet) * ratio)  # 计算子样本的大小while len(subdataSet) < lenSubdata:  # 当子样本未达到应有大小时index = randrange(len(dataSet) - 1)  # 随机选择数据集中的索引（有放回）subdataSet.append(dataSet[index])  # 将随机选择的数据加入子样本return subdataSet  # 返回子样本

分割数据集

#根据指定特征索引和分割值，将数据集划分为两个子集，是决策树等算法中用于划分节点的核心操作
# 分割数据集
def data_spilt(dataSet, index, value):left = []  # 创建存储左子集的列表right = []  # 创建存储右子集的列表for row in dataSet:  # 遍历数据集中的每一行if row[index] < value:  # 如果行中指定索引的值小于给定值left.append(row)  # 将该行添加到左子集else:right.append(row)  # 否则将该行添加到右子集return left, right  # 返回左右的子集

损失函数

#计算数据集分割后的 “不纯度”（Impurity），
# 用于衡量分割的优劣。它实现的是基尼不纯度（Gini Impurity） 的计算逻辑，是分类问题中评估决策树分割质量的常用指标。
def spilt_loss(left, right, class_values):loss = 0.0  # 初始化分割代价为0for class_value in class_values:  # 遍历每个类别的取值left_size = len(left)  # 计算左子集的大小if left_size != 0:  # 防止除数为零prop = [row[-1] for row in left].count(class_value) / float(left_size)  # 计算左子集中该类别的占比loss += (prop * (1.0 - prop))  # 根据占比计算损失right_size = len(right)  # 计算右子集的大小if right_size != 0:  # 防止除数为零prop = [row[-1] for row in right].count(class_value) / float(right_size)  # 计算右子集中该类别的占比loss += (prop * (1.0 - prop))  # 根据占比计算损失return loss  # 返回分割代价

选取分割时的最优特征

def get_best_spilt(dataSet, n_features):features = []  # 用于存储随机选择的特征的列表class_values = list(set(row[-1] for row in dataSet))  # 获取数据集中的类别值b_index, b_value, b_loss, b_left, b_right = 999, 999, 999, None, None  # 初始化最佳分割的特征索引、值、损失和左右子集while len(features) < n_features:  # 当特征列表中的特征数量小于n_features时index = randrange(len(dataSet[0]) - 1)  # 随机选择一个特征索引if index not in features:  # 如果选择的特征索引不在特征列表中features.append(index)  # 将特征索引添加到特征列表中for index in features:  # 遍历随机选择的特征for row in dataSet:  # 遍历数据集中的每一行left, right = data_spilt(dataSet, index, row[index])  # 根据特征和特征值将数据集分割成左右子集loss = spilt_loss(left, right, class_values)  # 计算分割代价if loss < b_loss:  # 如果当前分割代价比最小代价还小b_index, b_value, b_loss, b_left, b_right = index, row[index], loss, left, right  # 更新最佳分割信息return {'index': b_index, 'value': b_value, 'left': b_left, 'right': b_right}  # 返回最佳分割特征的索引、值、左右子集

确定最终的输出标签

#这个函数 decide_label 的作用是从输入数据中确定最终的输出标签，采用的是 “多数投票” 原则 —— 即选择数据中出现次数最多的标签作为结果
# 这在决策树等模型中常用于叶子节点的标签确定（当数据集无法再分割或达到停止条件时，用多数样本的标签作为该节点的预测结果）
def decide_label(data):output = [row[-1] for row in data]  # 获取数据中所有标签的列表return max(set(output), key=output.count)  # 返回出现次数最多的标签

子分割，不断地构建叶节点的过程

def sub_spilt(root, n_features, max_depth, min_size, depth):left = root['left']right = root['right']del (root['left'])del (root['right'])if not left or not right:root['left'] = root['right'] = decide_label(left + right)  # 如果左节点或右节点为空，则将左右节点设为出现次数最多的标签returnif depth > max_depth:root['left'] = decide_label(left)  # 如果深度超过最大深度，则将左节点设为出现次数最多的标签root['right'] = decide_label(right)  # 将右节点设为出现次数最多的标签returnif len(left) < min_size:root['left'] = decide_label(left)  # 如果左节点数据量小于最小数据量，则将左节点设为出现次数最多的标签else:root['left'] = get_best_spilt(left, n_features)  # 否则，根据最佳分割点构建左节点sub_spilt(root['left'], n_features, max_depth, min_size, depth + 1)  # 递归构造左子树if len(right) < min_size:root['right'] = decide_label(right)  # 如果右节点数据量小于最小数据量，则将右节点设为出现次数最多的标签else:root['right'] = get_best_spilt(right, n_features)  # 否则，根据最佳分割点构建右节点sub_spilt(root['right'], n_features, max_depth, min_size, depth + 1)  # 递归构造右子树

构造决策树

def build_tree(dataSet, n_features, max_depth, min_size):root = get_best_spilt(dataSet, n_features)  # 找到最佳分割点作为根节点sub_spilt(root, n_features, max_depth, min_size, 1)  # 构建整棵决策树return root  # 返回根节点

预测

def predict(tree, row):predictions = []  # 初始化一个存储预测结果的列表if row[tree['index']] < tree['value']:  # 如果数据的某个特征值小于当前节点的划分值if isinstance(tree['left'], dict):  # 如果左子树仍然是一个字典（即非叶子节点）return predict(tree['left'], row)  # 递归地对左子树进行预测else:  # 如果左子树是叶子节点return tree['left']  # 返回左子树的预测结果else:  # 如果数据的某个特征值大于或等于当前节点的划分值if isinstance(tree['right'], dict):  # 如果右子树仍然是一个字典（即非叶子节点）return predict(tree['right'], row)  # 递归地对右子树进行预测else:  # 如果右子树是叶子节点return tree['right']  # 返回右子树的预测结果

得到最终的预测值

#集成学习中 Bagging（ bootstrap aggregating）方法的预测函数，用于结合多棵决策树的预测结果，得到最终的预测值。
# 其核心思想是 **“多数投票”**—— 即综合多棵树的预测结果，选择出现次数最多的结果作为最终预测。
def bagging_predict(trees, row):predictions = [predict(tree, row) for tree in trees]  # 使用每棵树对数据进行预测，并将预测结果存储在列表中# 找到预测结果中出现次数最多的值作为最终预测结果return max(set(predictions), key=predictions.count)  # 找到预测结果中出现次数最多的值作为最终预测结果

创建随机森林

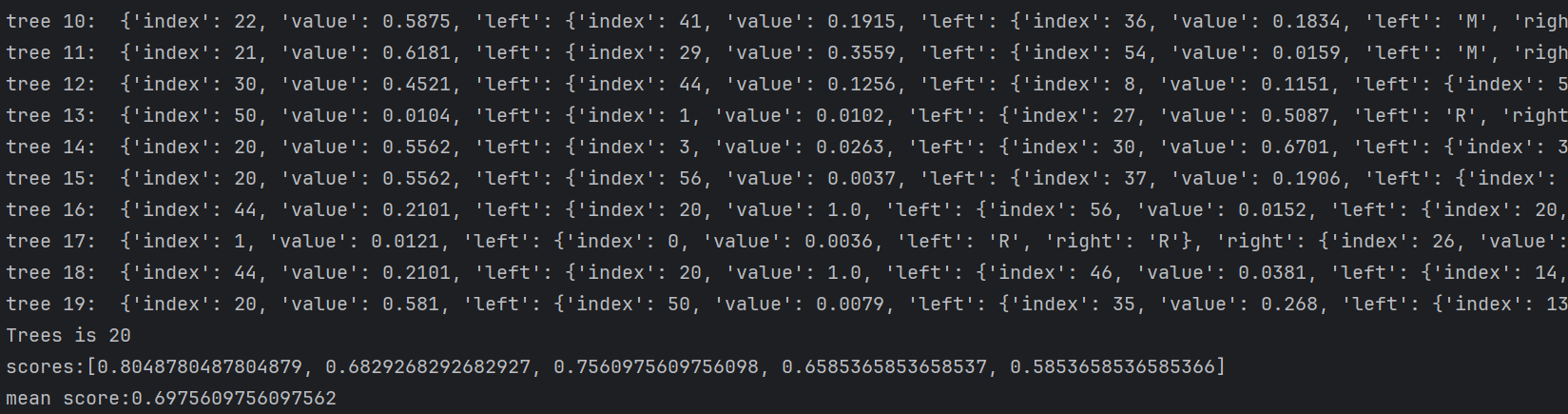
def random_forest(train, test, ratio, n_features, max_depth, min_size, n_trees):trees = []  # 用于存储每棵树的列表for i in range(n_trees):train = get_subsample(train, ratio)  # 从训练集中进行子采样tree = build_tree(train, n_features, max_depth, min_size)  # 构建一棵树print('tree %d: '%i,tree)trees.append(tree)  # 将构建好的树添加到列表中# predict_values = [predict(trees,row) for row in test]predict_values = [bagging_predict(trees, row) for row in test]  # 对测试集中的每一行数据进行预测return predict_values  # 返回预测结果列表

计算准确率

def accuracy(predict_values, actual):correct = 0  # 初始化正确预测的数量for i in range(len(actual)):  # 遍历每一个预测结果if actual[i] == predict_values[i]:  # 如果预测结果与实际结果相符correct += 1  # 正确预测数量加一return correct / float(len(actual))  # 返回正确预测的比例

主函数

if __name__ == '__main__':seed(1)  # 设置随机种子，以确保结果的可重复性dataSet = loadCSV('sonar-all-data.csv')  # 载入数据集column_to_float(dataSet)  # 将数据集中的数据类型转换为浮点型n_folds = 5  # 设置交叉验证的折数max_depth = 15  # 决策树的最大深度min_size = 1  # 叶子节点的最小样本数ratio = 1  # 子采样比例n_features = 15  # 特征数量n_trees = 20  # 随机森林中树的数量folds = spiltDataSet(dataSet, n_folds)  # 将数据集划分为指定折数的子集scores = []  # 用于存储每次交叉验证的准确率# 实现了k折交叉验证（k - foldcross - validation） 的核心逻辑，用于评估随机森林模型的性能。它将数据集分成多个子集（fold），# 每次用其中一个子集作为测试集，其余作为训练集，循环验证并计算模型准确率，最终得到多个准确率分数用于评估模型稳定性。for fold in folds:  # 对每个子集进行交叉验证train_set = folds[:]  # 复制数据集train_set.remove(fold)  # 从训练集中移除当前折的数据train_set = sum(train_set, [])  # 将多个fold列表组合成一个train_set列表test_set = [list(row)[:-1] for row in fold]  # 从当前折中提取测试数据actual = [row[-1] for row in fold]  # 获取当前折的实际结果predict_values = random_forest(train_set, test_set, ratio, n_features, max_depth, min_size,n_trees)  # 使用随机森林进行预测accur = accuracy(predict_values, actual)  # 计算准确率scores.append(accur)  # 将准确率添加到列表中print('Trees is %d' % n_trees)  # 打印树的数量print('scores:%s' % scores)  # 打印每次交叉验证的准确率print('mean score:%s' % (sum(scores) / float(len(scores))))  # 打印平均准确率

http://www.dtcms.com/a/361485.html

相关文章：

  • AUTOSAR AP R24-11 Log and Trace 文档总结
  • 贪心算法解决钱币找零问题(二)
  • CentOS10安装RabbitMQ
  • [特殊字符]【C语言】超全C语言字符串处理函数指南：从原理到实战
  • ARM的编程模型
  • TikTok Shop 物流拖后腿？海外仓系统破解物流困局
  • nginx是什么？
  • MQ使用场景分析
  • OpenHarmony 分布式感知中枢深度拆解：MSDP 框架从 0 到 1 的实战指南
  • 2025年- H104-Lc212--455.分发饼干(贪心)--Java版
  • 电动自行车淋水安全测试的关键利器：整车淋水性能测试装置的技术分析
  • 零基础深度学习技术学习指南：从入门到实践的完整路径
  • 大语言模型对齐
  • 中宇联SASE解决方案荣获最佳实践奖，助力国际零售企业数字化转型
  • 像信号处理一样理解中断:STM32与RK3399中断机制对比及 Linux 驱动开发实战
  • Kali自带的录屏工具：recordmydesktop
  • 响应式编程框架Reactor【8】
  • LINUX 91 SHELL:删除空文件夹 计数
  • 【C++】内存管理机制：从new到delete全解析
  • 如何对嵌入式软件进行单元测试
  • 增强现实—Gated-attention architectures for task-oriented language grounding
  • 8K4K图像评估平台
  • Shader开发（十九）统一变量纹理亮度调节
  • 永磁同步电机无速度算法--高频脉振方波注入法（新型位置跟踪策略）
  • Linux常用命令行大全：14个核心指令详解+实战案例
  • 第8篇c++Expression: (L“Buffer is too small“ 0
  • LintCode第401题-排序矩阵中的从小到大第k个数
  • ESP32驱动数字麦克风INMP441
  • 如何解决pip安装报错ModuleNotFoundError: No module named ‘tox’问题
  • 代码随想录刷题Day47