C++ 面试高频考点 力扣 35. 搜索插入位置 二分查找 左右端点查找 题解 每日一题

题目描述

题目链接：
力扣35. 搜索插入位置

题目描述：

示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4

注意：
时间复杂度为 O(log n)

为什么这道题值得弄懂？

再前面的三篇博客中我们都是通过题目来练习二分查找的，那么这道题目也不例外，我们依然通过这道题来练习二分，这道题目虽然是简单题思路好想，那么我们就可以通过在这道题的练习中梳理二分再写代码的时候会遇到的细节问题

为什么可以用二分？

首先我们可以思考为什么这道题可以用二分？
我们来看题目，首先这道题的已知是排序数组，并且给一个目标值，这是一个在有序数组中查找指定数的问题，我们就可以通过二段性来进行舍弃不符合条件的部分，并且“二分查找的核心是利用数组的‘二段性’—— 将数组分为‘满足条件’和‘不满足条件’的两部分，每次舍弃其中一部分，从而将时间复杂度压缩到 O (log n)

二分查找的两种实现思路（左端点定位 vs 右端点定位）

二分查找的关键是定义 “满足条件的区间”，并通过指针移动逐步缩小区间，最终定位到目标位置。本题中，目标位置有两种解读：

• 左端点定位：找 “最后一个小于等于 target 的元素位置”，再根据该位置判断插入点；
• 右端点定位：找 “第一个大于等于 target 的元素位置”，该位置直接就是插入点（若元素存在，就是元素索引）。

下面分别展开两种思路的细节分析。

思路一：左端点定位（找“最后一个≤target的元素”）

1. 二段性划分
将数组分为两部分：

• 左半部分（满足条件）：nums[i] ≤ target（目标值若存在，必在这部分；若不存在，插入点在这部分的最后一个元素之后）；
• 右半部分（不满足条件）：nums[i] > target（这部分元素都比target大，可直接舍弃）。

示例：若nums = [1,3,5,6]，target = 2，则满足条件的区间是[1]（1≤2），不满足条件的区间是[3,5,6]（3>2）。

2. 指针移动逻辑

• right指针：若nums[middle] > target，说明middle及右侧都属于“不满足条件的右半部分”，直接舍弃，故right = middle - 1；
• left指针：若nums[middle] ≤ target，说明middle及左侧属于“满足条件的左半部分”，需保留middle（可能是最后一个满足条件的元素），故left = middle（而非middle + 1，避免漏掉目标）。

3. 循环结束条件
循环条件设为left < right，当left == right时，区间缩小到唯一元素，该元素就是“最后一个≤target的元素”，循环结束。

4. 中间值（middle）的取法
必须用向上取整：middle = left + (right - left + 1) / 2（等价于(left + right + 1) // 2，避免整数溢出）。

为什么不用向下取整（left + (right - left)/2）？
若用向下取整，当区间长度为2时（如left=2, right=3，对应nums=[5,6]，target=5）：

• 计算middle = 2 + (3-2)/2 = 2；
• 因nums[2] = 5 ≤ 5，执行left = middle = 2；
• 此时left仍等于2，right等于3，循环条件left < right仍成立，陷入死循环。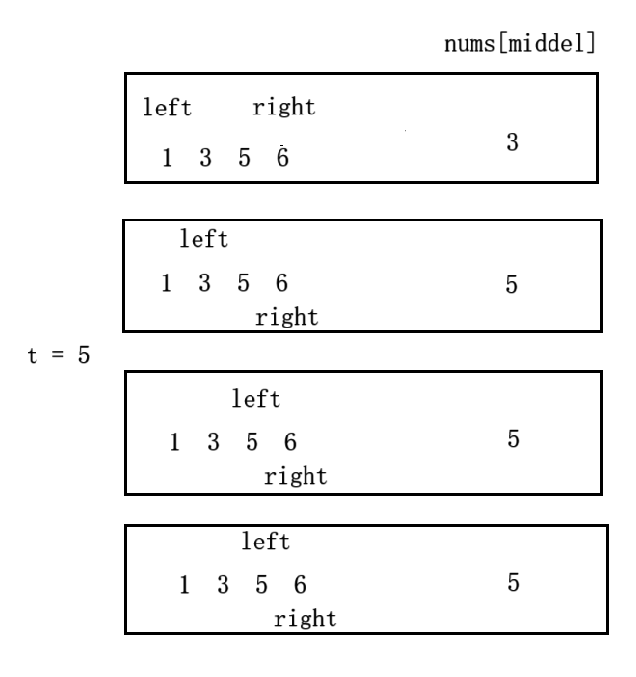
• 

而向上取整会避免这种情况：＜（＾－＾）＞

• 同样left=2, right=3，middle = 2 + (3-2+1)/2 = 3；
• 若nums[3] = 6 > 5，执行right = 3-1 = 2；
• 此时left == right，循环结束，无死循环。

5. 最终插入点计算
循环结束后，left == right，指向“最后一个≤target的元素”，需分两种情况：

• 若nums[left] == target：直接返回left（目标值存在）；
• 若nums[left] < target：插入点在left + 1（如target=7，最后一个≤7的元素是6，索引3，插入点4=3+1）；
• （补充：nums[left] > target的情况不存在！因为left是“最后一个≤target的元素”，不可能大于target，原文此处判断冗余，可删除）。

简化后返回逻辑：return nums[left] == target ? left : left + 1。

思路二：右端点定位（找“第一个≥target的元素”）

1. 二段性划分
将数组分为两部分：

• 左半部分（不满足条件）：nums[i] < target（这部分元素都比target小，可直接舍弃）；
• 右半部分（满足条件）：nums[i] ≥ target（目标值若存在，必在这部分的第一个位置；若不存在，这部分的第一个位置就是插入点）。

示例：若nums = [1,3,5,6]，target = 2，则不满足条件的区间是[1]（1<2），满足条件的区间是[3,5,6]（3≥2），第一个满足条件的元素是3，索引1，即插入点1（与示例2结果一致）。

2. 指针移动逻辑

• left指针：若nums[middle] < target，说明middle及左侧都属于“不满足条件的左半部分”，直接舍弃，故left = middle + 1；
• right指针：若nums[middle] ≥ target，说明middle及右侧属于“满足条件的右半部分”，需保留middle（可能是第一个满足条件的元素），故right = middle（而非middle - 1，避免漏掉目标）。

3. 循环结束条件
与左端点定位一致，循环条件设为left < right，当left == right时，区间缩小到唯一元素，该元素就是“第一个≥target的元素”，循环结束。

4. 中间值（middle）的取法
必须用向下取整：middle = left + (right - left) / 2（等价于(left + right) // 2）。

为什么不能用向上取整？
若用向上取整，当区间长度为2时（如left=0, right=1，对应nums=[1,3]，target=2）：

• 计算middle = 0 + (1-0+1)/2 = 1；
• 因nums[1] = 3 ≥ 2，执行right = middle = 1；
• 此时left=0，right=1，循环条件left < right仍成立，陷入死循环。

而向下取整会避免这种情况：

• 同样left=0, right=1，middle = 0 + (1-0)/2 = 0；
• 因nums[0] = 1 < 2，执行left = 0 + 1 = 1；
• 此时left == right，循环结束，无死循环。

5. 最终插入点计算
循环结束后，left == right，指向“第一个≥target的元素”，该位置直接就是答案：

• 若nums[left] == target：返回left（目标值存在）；
• 若nums[left] > target：返回left（目标值不存在，插入点就是第一个比target大的元素位置）；
• （特殊情况：若target比所有元素都大，如target=7，nums=[1,3,5,6]，则循环后left=4？不，初始right = nums.size()-1 = 3，循环中nums[middle] <7，left逐步移到3，最终left=3，nums[3]=6 <7？此处需纠正：当target比所有元素大时，“第一个≥target的元素”不存在于数组中，插入点是nums.size()，但循环后left会等于nums.size()-1，且nums[left] < target，故需补充判断：若nums[left] < target，返回left + 1）。

最终返回逻辑：return nums[left] >= target ? left : left + 1（可简化为return left，因为当nums[left] < target时，left已是nums.size()-1，left +1 = nums.size()，符合插入点要求）。

代码实现

代码1：左端点定位（找“最后一个≤target的元素”）

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;// 循环缩小区间，找最后一个<=target的元素while (left < right) {// 向上取整，避免死循环int middle = left + (right - left + 1) / 2;if (nums[middle] > target) {// 舍弃右半部分（middle及右侧）right = middle - 1;} else {// 保留左半部分（middle及左侧）left = middle;}}// 最终left == right，判断插入点return nums[left] == target ? left : left + 1;}
};

代码2：右端点定位（找“第一个≥target的元素”）

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;// 循环缩小区间，找第一个>=target的元素while (left < right) {// 向下取整，避免死循环int middle = left + (right - left) / 2;if (nums[middle] < target) {// 舍弃左半部分（middle及左侧）left = middle + 1;} else {// 保留右半部分（middle及右侧）right = middle;}}// 最终left == right，直接返回（若nums[left]<target，说明target比所有元素大，left+1 = nums.size()）return nums[left] >= target ? left : left + 1;// 简化写法：return left; （原因见思路二的5点分析）}
};

总结：二分查找的关键细节

1. 二段性是核心：先明确“满足条件的区间”是什么（如“≤target”或“≥target”），再确定舍弃哪部分；
2. 中间值取整决定死循环：
   • 若left = middle（保留左半部分），必须用向上取整（避免区间长度为2时死循环）；
   • 若right = middle（保留右半部分），必须用向下取整（同理）；
3. 最终位置判断：左端点定位需判断“是否等于target”，右端点定位可直接返回（因“第一个≥target的位置”就是插入点）。

通过这道题，能彻底理清二分查找中“指针移动”和“中间值取整”的逻辑，后续遇到更复杂的二分问题（如找重复元素的左边界/右边界）也能举一反三。