[信号与系统个人笔记]第三章 连续时间信号与系统的频域分析
Update
- 2025.8.31
- 3.1 连续时间周期信号的傅里叶级数
3.1连续时间周期信号的傅里叶级数
狄利克雷条件:
在一个周期内:{函数连续或只有有限个第一类间断点有有限个极大、极小值函数绝对可积
\begin{align}
&在一个周期内 :
\begin{cases}
函数连续或只有有限个第一类间断点\\ \\
有有限个极大、极小值\\ \\
函数绝对可积
\end{cases}
\end{align}
在一个周期内:⎩⎨⎧函数连续或只有有限个第一类间断点有有限个极大、极小值函数绝对可积
三角形式的傅里叶级数
三角形式傅里叶级数的定义
给定周期为TTT的周期信号f(t)f(t)f(t),当满足狄利克雷条件时,可以表示为(t0,t0+T)(t_{0},t_{0}+T)(t0,t0+T)上的完备正交函数集合{1,cosnΩt,sinnΩt} (n→∞,Ω=2πT)\{ 1,\cos n\Omega t,\sin n\Omega t \}\ \left( n\to \infty,\Omega=\frac{2\pi}{T} \right){1,cosnΩt,sinnΩt} (n→∞,Ω=T2π)中各个函数的线性组合 :
f(t)=a02+∑n=1∞(ancosnΩt+bnsinnΩt)
f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}(a_{n}\cos n\Omega t+b_{n}\sin n\Omega t)
f(t)=2a0+n=1∑∞(ancosnΩt+bnsinnΩt)
其中:
- 直流分量:a02\frac{a_{0}}{2}2a0
- nnn次余弦分量:ancosnΩta_{n}\cos n\Omega tancosnΩt,nnn次正弦分量:bnsinnΩtb_{n}\sin n\Omega tbnsinnΩt
- 基波角频率:Ω=2πT\Omega=\frac{2\pi}{T}Ω=T2π
- 基波频率:f=1Tf=\frac{1}{T}f=T1
a02=1T∫t0t0+Tf(t)dtan=2T∫t0t0+Tf(t)cosnΩtdtbn=2T∫t0t0+Tf(t)sinnΩtdt \begin{align} &\frac{a_{0}}{2}=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)dt\\ \\ &a_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\cos n\Omega tdt\\ \\ &b_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\sin n\Omega tdt \end{align} 2a0=T1∫t0t0+Tf(t)dtan=T2∫t0t0+Tf(t)cosnΩtdtbn=T2∫t0t0+Tf(t)sinnΩtdt
三角级数的直流、基波、谐波分量
同频率项合并:(辅助角)
f(t)=A02+∑n=1∞Ancos(nΩt+φn)其中:A0=a0,An=an2+bn2,φn=−arctanbnanan=Ancosφn,bn=−Ansinφn
\begin{align}
&f(t)=\frac{A_{0}}{2}+\sum_{n=1}^{\infty}A_{n}\cos(n\Omega t+\varphi_{n})\\ \\
&其中:\\ \\
&A_{0}=a_{0},A_{n}=\sqrt{ a_{n}^{2}+b_{n}^{2} },\varphi_{n}=-\arctan \frac{b_{n}}{a_{n}}\\ \\
&a_{n}=A_{n}\cos \varphi_{n},b_{n}=-A_{n}\sin \varphi_{n}
\end{align}
f(t)=2A0+n=1∑∞Ancos(nΩt+φn)其中:A0=a0,An=an2+bn2,φn=−arctananbnan=Ancosφn,bn=−Ansinφn
上式表明:任何满足狄利克雷条件的周期信号都可以分解为直流分量,基波分量和无穷多项谐波分量之和。其中各次谐波分量的角频率必然是基波频率的整数倍
直流分量:A02=a02=1T∫t0t0+Tf(t)dt基波分量(n=1):A1cos(Ωt+φ1)n次谐波分量(n≠1):Ancos(nΩt+φn)
\begin{align}
&直流分量:\frac{A_{0}}{2}=\frac{a_{0}}{2}=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)dt\\ \\
&基波分量(n=1):A_{1}\cos(\Omega t+\varphi_{1})\\ \\
&n次谐波分量(n\neq 1):A_{n}\cos(n\Omega t+\varphi_{n})
\end{align}
直流分量:2A0=2a0=T1∫t0t0+Tf(t)dt基波分量(n=1):A1cos(Ωt+φ1)n次谐波分量(n=1):Ancos(nΩt+φn)
f(t)=直流+基波+谐波
f(t)=直流+基波+谐波
f(t)=直流+基波+谐波
傅里叶系数的奇偶性
将系数视为谐波次数nnn或者nnn倍基波角频率nΩn\OmeganΩ的函数,以nnn或者nΩn\OmeganΩ为自变量进行分析:
an=2T∫t0t0+Tf(t)cosnΩtdta−n=an为n的偶函数bn=2T∫t0t0+Tf(t)sinnΩtdtb−n=−bn为n的奇函数An=an2+bn2A−n=An为n的偶函数φn=−arctanbnanφ−n=−φn为n的奇函数
\begin{align}
&a_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\cos n\Omega tdt\quad a_{-n}=a_{n}\quad 为n的偶函数\\ \\
&b_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)\sin n\Omega tdt\quad b_{-n}=-b_{n}\quad 为n的奇函数\\ \\
&A_{n}=\sqrt{ a_{n}^{2}+b_{n}^{2} }\quad A_{-n}=A_{n}\quad 为n的偶函数\\ \\
&\varphi_{n}=-\arctan \frac{b_{n}}{a_{n}}\quad \varphi_{-n}=-\varphi_{n}\quad 为n的奇函数
\end{align}
an=T2∫t0t0+Tf(t)cosnΩtdta−n=an为n的偶函数bn=T2∫t0t0+Tf(t)sinnΩtdtb−n=−bn为n的奇函数An=an2+bn2A−n=An为n的偶函数φn=−arctananbnφ−n=−φn为n的奇函数
信号的对称性与傅里叶系数的关系
信号为ttt的偶函数
- f(t)cosnΩtf(t)\cos n\Omega tf(t)cosnΩt为偶函数,f(t)sinnΩtf(t)\sin n\Omega tf(t)sinnΩt为奇函数
- an=2T∫−T2T2f(t)cosnΩtdt=4T∫0T2f(t)cosnΩtdta_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\cos n\Omega tdt=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(t)\cos n\Omega tdtan=T2∫−2T2Tf(t)cosnΩtdt=T4∫02Tf(t)cosnΩtdt
- bn=2T∫−T2T2f(t)sinnΩtdt=0b_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\sin n\Omega tdt=0bn=T2∫−2T2Tf(t)sinnΩtdt=0
- 此时,傅里叶级数不包含正弦项:f(t)=a02+∑n=1∞ancosnΩtf(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\cos n\Omega tf(t)=2a0+∑n=1∞ancosnΩt
信号为ttt的奇函数
- f(t)cosnΩtf(t)\cos n\Omega tf(t)cosnΩt为奇函数,f(t)sinnΩtf(t)\sin n\Omega tf(t)sinnΩt为偶函数
- an=2T∫−T2T2f(t)cosnΩtdt=0a_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\cos n\Omega tdt=0an=T2∫−2T2Tf(t)cosnΩtdt=0
- bn=2T∫−T2T2f(t)sinnΩtdt=4T∫0T2f(t)sinnΩtdtb_{n}=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\sin n\Omega tdt=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(t)\sin n\Omega tdtbn=T2∫−2T2Tf(t)sinnΩtdt=T4∫02Tf(t)sinnΩtdt
- 此时,傅里叶级数不包含直流和余弦项:f(t)=∑n=1∞bnsinnΩtf(t)=\sum_{n=1}^{\infty}b_{n}\sin n\Omega tf(t)=∑n=1∞bnsinnΩt
信号为半波对称函数
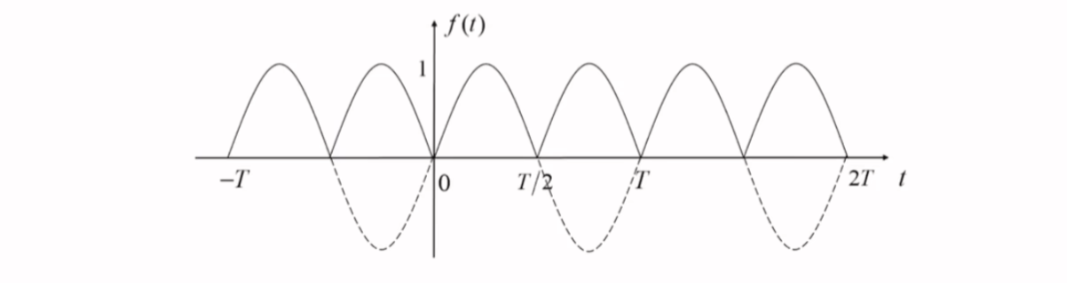
f(t)=f(t±T2)f(t)=f\left( t\pm \frac{T}{2} \right)f(t)=f(t±2T)信号沿时间轴平移半个周期以后与原波形完全重合
Ω=2πT ⟹ Ω′=2πT2=4πT=2Ω
\Omega=\frac{2\pi}{T}\implies \Omega'=\frac{2\pi}{\frac{T}{2}}=\frac{4\pi}{T}=2\Omega
Ω=T2π⟹Ω′=2T2π=T4π=2Ω
- 信号实际周期为T2\frac{T}{2}2T,2Ω2\Omega2Ω为实际的基波角频率,故只含有Ω\OmegaΩ的偶次谐波
- 此时傅里叶级数只含有偶次谐波,不含奇次谐波,又称为偶谐函数
- 此处的偶谐函数是相对于原函数而言的,因为实际上可以直接令T′=T2T'=\frac{T}{2}T′=2T
信号为半波镜像对称函数
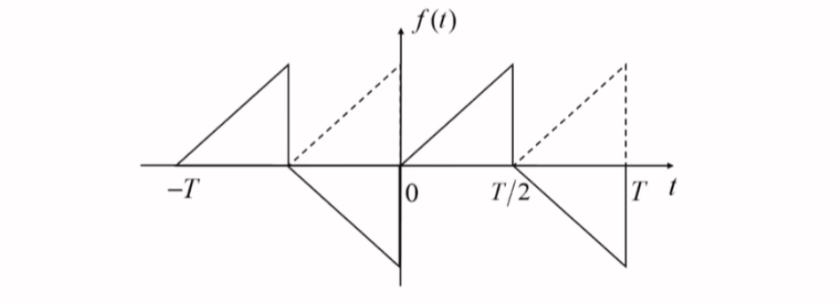
f(t)=−f(t±T2)f(t)=-f\left( t\pm \frac{T}{2} \right)f(t)=−f(t±2T)信号平移半个周期以后与原波形关于横轴对称
a0=a2=⋯=a2n=b0=b2=⋯=b2n=0a1,a3,…,a2n+1,b1,b3,…,b2n+1≠0 \begin{align} &a_{0}=a_{2}=\dots=a_{2n}=b_{0}=b_{2}=\dots=b_{2n}=0\\ \\ &a_{1},a_{3},\dots,a_{2n+1},b_{1},b_{3},\dots,b_{2n+1}\neq 0 \end{align} a0=a2=⋯=a2n=b0=b2=⋯=b2n=0a1,a3,…,a2n+1,b1,b3,…,b2n+1=0
- 此时傅里叶级数只含有奇次谐波,不含偶次谐波,又称为奇谐函数
任意信号分解为偶分量和奇分量之和
f(t)=f(t)+f(−t)2+f(t)−f(−t)2=fev(t)+fod(t)
f(t)= \frac{f(t)+f(-t)}{2}+ \frac{f(t)-f(-t)}{2}=f_{ev}(t)+f_{od}(t)
f(t)=2f(t)+f(−t)+2f(t)−f(−t)=fev(t)+fod(t)
其中:
- ev→even,od→oddev\to even,od\to oddev→even,od→odd
- 偶分量:fev(t)=f(t)+f(−t)2f_{ev}(t)=\frac{f(t)+f(-t)}{2}fev(t)=2f(t)+f(−t)
- 奇分量:fod(t)=f(t)−f(−t)2f_{od}(t)= \frac{f(t)-f(-t)}{2}fod(t)=2f(t)−f(−t)
指数形式的傅里叶级数
指数形式的傅里叶级数的定义
给定周期为TTT的周期信号f(t)f(t)f(t),当它满足狄利克雷条件时,可以表示为(t0,t0+T)(t_{0},t_{0}+T)(t0,t0+T)上完备正交函数集合{ejnΩt}(n→∞,Ω=2πT)\{ e^{jn\Omega t} \}\left( n\to \infty,\Omega=\frac{2\pi}{T} \right){ejnΩt}(n→∞,Ω=T2π)中各个函数的线性组合:
f(t)=∑n=−∞∞FnejnΩtFn=1T∫t0t0+Tf(t)e−jnΩtdt
\begin{align}
&f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}\\ \\
&F_{n}=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)e^{-jn\Omega t}dt
\end{align}
f(t)=n=−∞∑∞FnejnΩtFn=T1∫t0t0+Tf(t)e−jnΩtdt
指数形式傅里叶级数中出现了负频率,负频率没有实际的物理意义,它的出现完全是采用复指数信号集合表示周期信号的结果,是数学分析的过程,当正负频率合并在一起的时候才能合成实际的频率分量
指数形式与三角形式傅里叶系数的关系
Fn=1T∫t0t0+Tf(t)e−jnΩtdt=1T∫t0t0+Tf(t)cosnΩtdt−j1T∫t0t0+Tf(t)sinnΩtdt=12(an−jbn)F−n=12(a−n−jb−n)=12(an+jbn) ⟹ {an=Fn+F−nbn=j(Fn−F−n) \begin{align} F_{n}&=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)e^{-jn\Omega t}dt=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)\cos n\Omega tdt-j \frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)\sin n\Omega tdt\\ \\ &=\frac{1}{2}(a_{n}-jb_{n})\\ \\ F_{-n}&=\frac{1}{2}(a_{-n}-jb_{-n})=\frac{1}{2}(a_{n}+jb_{n})\\ \\ \implies&\begin{cases} a_{n}=F_{n}+F_{-n}\\ \\ b_{n}=j(F_{n}-F_{-n}) \end{cases} \end{align} FnF−n⟹=T1∫t0t0+Tf(t)e−jnΩtdt=T1∫t0t0+Tf(t)cosnΩtdt−jT1∫t0t0+Tf(t)sinnΩtdt=21(an−jbn)=21(a−n−jb−n)=21(an+jbn)⎩⎨⎧an=Fn+F−nbn=j(Fn−F−n)
对于复数FnF_{n}Fn,可以转换为Fn=∣Fn∣⋅ej⋅∠FnF_{n}=|F_{n}|\cdot e^{j\cdot\angle F_{n}}Fn=∣Fn∣⋅ej⋅∠Fn
∣Fn∣=12an2+bn2=12An , ∣Fn∣=∣F−n∣为n的偶函数∠Fn=−arctanbnan=φn , φ−n=−φn为n的奇函数∴Fn=12Anejφn
\begin{align}
&|F_{n}|=\frac{1}{2}\sqrt{ a_{n}^{2}+b_{n}^{2} }=\frac{1}{2}A_{n}\ ,\ |F_{n}|=|F_{-n}|\quad 为n的偶函数\\ \\
&\angle F_{n}=-\arctan \frac{b_{n}}{a_{n}}=\varphi_{n}\ ,\ \varphi_{-n}=-\varphi_{n}\quad 为n的奇函数\\ \\
&\therefore F_{n}=\frac{1}{2}A_{n}e^{j\varphi_{n}}
\end{align}
∣Fn∣=21an2+bn2=21An , ∣Fn∣=∣F−n∣为n的偶函数∠Fn=−arctananbn=φn , φ−n=−φn为n的奇函数∴Fn=21Anejφn
例
求图示周期信号的指数形式傅里叶级数
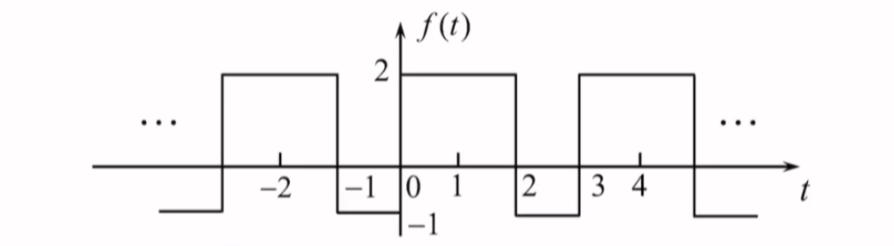
T=3,Ω=2πT=2π3Fn=1T∫0Tf(t)e−jnΩtdt=13[2∫02e−jnΩtdt−∫23e−jnΩtdt]=23⋅1j⋅3nΩe−jnΩt∣02−13⋅1−j⋅nΩe−jnΩt∣23=2−3e−j⋅2nΩ+e−j⋅3nΩj⋅3nΩ将Ω=2π3代入得:原式=2−3e−j⋅4π3n+e−j⋅2πnj⋅2πn由于e−j⋅2πn=cos2πn−j⋅sin2πn=1:原式=3j⋅2πn(1−ej⋅4π3n)∴f(t)=∑n=−∞∞FnejnΩt=∑n=−∞∞3j⋅2πn(1−ej⋅4π3n)ejn2π3t \begin{align} &T=3,\Omega=\frac{2\pi}{T}=\frac{2\pi}{3}\\ \\ F_{n}&=\frac{1}{T}\int_0^{T}f(t)e^{-jn\Omega t} dt=\frac{1}{3}\left[ 2\int_{0}^{2}e^{-jn\Omega t}dt-\int_{2}^{3}e^{-jn\Omega t}dt \right]\\ \\ &=\frac{2}{3}\cdot \frac{1}{j\cdot3n\Omega}e^{-jn\Omega t}\bigg|_{0}^{2}-\frac{1}{3}\cdot \frac{1}{-j\cdot n\Omega}e^{-jn\Omega t}\bigg|_{2}^{3}\\ \\ &=\frac{2-3e^{-j\cdot 2n\Omega}+e^{-j\cdot 3n\Omega}}{j\cdot 3n\Omega}\\ \\ &将\Omega=\frac{2\pi}{3}代入得:\\ \\ 原式&=\frac{2-3e^{-j\cdot \frac{4\pi}{3}n}+e^{-j\cdot 2\pi n}}{j\cdot 2\pi n}\\ \\ &由于e^{-j\cdot 2\pi n}=\cos_{}2\pi n-j\cdot \sin 2\pi n=1:\\ \\ 原式&=\frac{3}{j\cdot 2\pi n}\left( 1-e^{j\cdot \frac{4\pi}{3}n} \right)\\ \\ &\therefore f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}=\sum_{n=-\infty}^{\infty}\frac{3}{j\cdot 2\pi n}\left( 1-e^{j\cdot \frac{4\pi}{3}n} \right)e^{jn \frac{2\pi}{3}t} \end{align} Fn原式原式T=3,Ω=T2π=32π=T1∫0Tf(t)e−jnΩtdt=31[2∫02e−jnΩtdt−∫23e−jnΩtdt]=32⋅j⋅3nΩ1e−jnΩt02−31⋅−j⋅nΩ1e−jnΩt23=j⋅3nΩ2−3e−j⋅2nΩ+e−j⋅3nΩ将Ω=32π代入得:=j⋅2πn2−3e−j⋅34πn+e−j⋅2πn由于e−j⋅2πn=cos2πn−j⋅sin2πn=1:=j⋅2πn3(1−ej⋅34πn)∴f(t)=n=−∞∑∞FnejnΩt=n=−∞∑∞j⋅2πn3(1−ej⋅34πn)ejn32πt
- 在最后一步化简的时候,可以将复数展开为三角形式,判断是否可以进一步整理成常数
