当前位置：首页 > news >正文

2024年山东省信息学小学组（CSP-X）第一轮题解

news 2025/8/29 7:53:21

2024年山东省信息学小学组（CSP-X）第一轮题解

原题下载
单项选择题
阅读程序
- 阅读程序 #1
- - 判断题
- 阅读程序 #2
- - 判断题
  - 单选题
- 阅读程序 #3
- - 判断题
  - 单选题
完善程序
- 消灭怪兽
- 位运算操作

原题下载

CSP-X2024小学组（山东）第一轮试题以及答案

单项选择题

共 15 题，每题 2 分，共计 30 分；每题有且仅有一个正确选项。

$2024)_{10}+(2F)_{16}$ 的运算结果是（）。

A. $100000010110)_2$
B. $816)_{16}$
C. $2071)_{10}$
D. $4026)_8$

解析： $2F)_{16}=47_{10}+2024_{10}=2071_{10}$ 。

执行完一下代码后，c的值是（）。

int a = 9, b = 6, c;
c = a / b + 0.5;

A. 1.5
B. 2
C. 2.0
D. 1

解析：c = a / b + 0.5;，a,b,c都是int类型，因此a / b结果为1，加上0.5之后赋值给c，c的值为1。

将数组{7, 20, 4, 16, 88, 0, 55, 100}中的元素按从大到小的顺序排列，每次可以交换任意两个元素，最少需要交换（）次。

A. 4
B. 5
C. 6
D. 7

解析：需要将数组元素按从大到小的顺序排列，要求每次可以交换任意两个元素，可以使用选择排序的思想：

第 $1$ 次将100和7交换，得到{100, 20, 4, 16, 88, 0, 55, 7}
第 $2$ 次将88和20交换，得到{100, 88, 4, 16, 20, 0, 55, 7}
第 $3$ 次将55和4交换，得到{100, 88, 55, 16, 20, 0, 4, 7}
第 $4$ 次将20和16交换，得到{100, 88, 55, 20, 16, 0, 4, 7}
第 $5$ 次将7和0交换，得到{100, 88, 55, 20, 16, 7, 4, 0}

最少需要交换5次。
4. 若待排序对象序列在排序前已按其排序码递增顺序排序，则采用（）方法比较次数最少。

A. 直接插入排序
B. 快速排序
C. 归并排序
D. 直接选择排序

解析：若有 $n$ 个待排序对象，在排序前已按其排序码递增顺序排序，那么

直接插入排序，需要比较 $n$ 次
快速排序，需要递归 $l o g n$ 层，在每一层将元素与基准值比较，进行分区操作，因此比较次数接近 $n\times logn$
归并排序，需要递归 $l o g n$ 层，在每一层需要合并 $n$ 个元素，因此比较次数接近 $n\times logn$
直接选择排序，每次需要选出最小值与当前位置上的元素进行交换，比较次数接近 $n^2$

设有一个 $100$ 阶的对称矩阵保存在二维数组a[100][100]，满足a[i][j]=a[j][i]，如果采用压缩存储方式按行将矩阵的下三角部分的元素存入一维数组b[]中，a[0][0]存入b[0]中，则a[10][5]在b[]中（）位置。

A. $50$
B. $60$
C. $51$
D. $61$

解析：如果将对称矩阵保存到二维数组a[100][100]，并采用压缩存储方式按行将矩阵的下三角部分的元素存入一维数组b[]中，如下图所示：
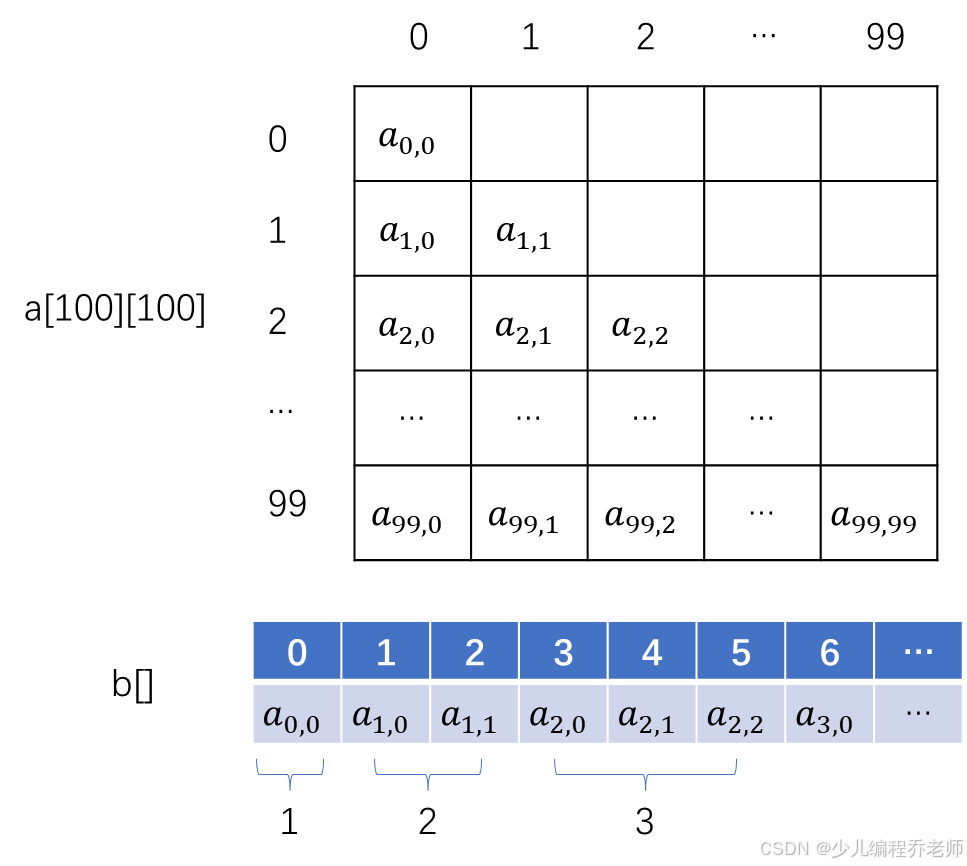
在这里插入图片描述
从第 $0$ 行开始，每行存入到b[]数组的元素个数为 $1, 2, 3...$ 的等差数列，那么 $0\sim 9$ 行一共存入 $\frac{(1+10)*10}{2}=55$ 个数，到a[10][5]还有 $6$ 个数，那么a[10][5]会存入b[60]。