Two Knights (数学)
题目:
思路:
前置知识:国际象棋中骑士的走法类比象棋的马,但是不会被棋子所阻挡
首先我们不考虑限制安排两个骑士,那么一共有 个格子,所以根据组合数学,那么就有
种选择方式,这是显然的
那么现在加上限制,现在两个骑士不能在二者的攻击范围内,由于二者是相对的,因此我们考虑其中一种情况即可,所以考虑分析其特点
我们发现只有在 2*3 或 3*2 的范围中二者才有可能在攻击范围内,即以下情况
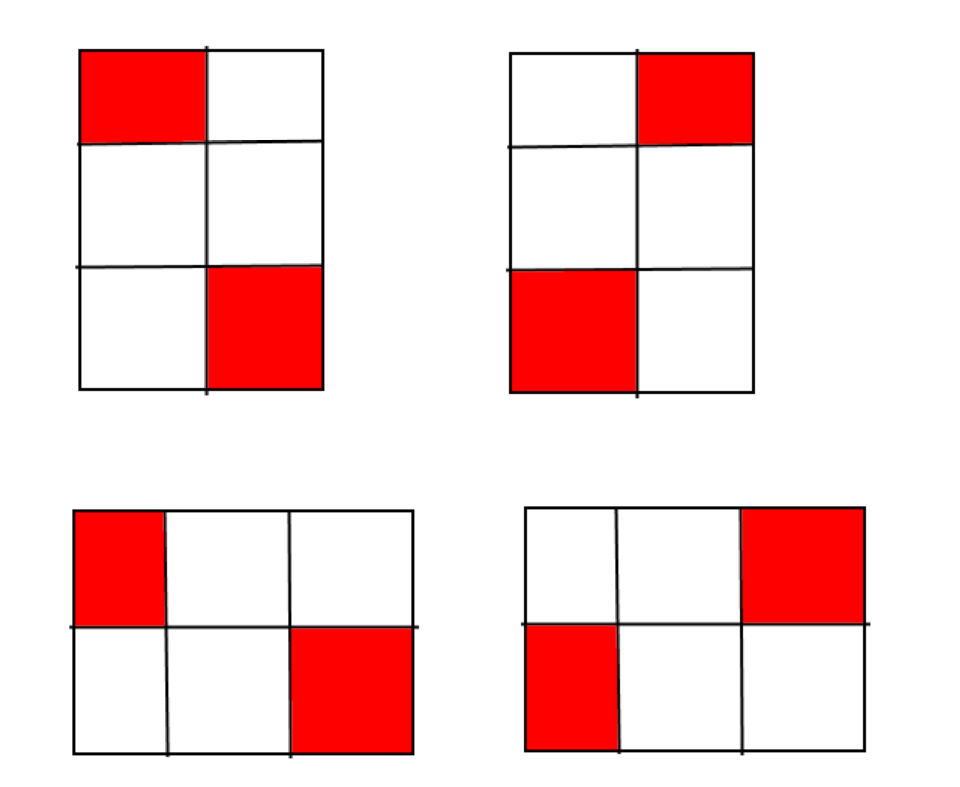
那么针对 2*3 的情况分析,我们有两种可能的攻击放法,那么在棋盘中有多少个 2*3 小块(假设为cnt)我们就有 2*cnt 种攻击方法
所以现在问题转变为求有多少个 2*3 的小方块,这也很简单,我们分开轴考虑,对于 2,我们一共有 (k-1) 种方法,同理对于 3,我们有 (k-2) 种放法
综上,根据乘法原理,我们方法数就有 2*(k-1)*(k*2) 种
同时还有 3*2 的情况,所以其实是 4*(k-1)*(k*2)
最后模拟即可,不过也能预处理答案,本题没有多测,其实也没必要
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"int getans(int k)
{int kk = k*k;int res = kk * (kk - 1) / 2;res -= 4 * (k-1)*(k-2);return res;
}void solve()
{int n;cin >> n;for (int i = 1; i <= n; i++){cout << getans(i) << endl;}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}