【电路笔记 通信】子载波的频域Sinc函数证明 OFDM 正交子载波证明 绘图示例

• OFDM 的子载波虽然在频域上频谱重叠，但彼此不会干扰， OFDM构造了一组短时的正交基函数。

子载波的频域波形是 Sinc 函数

• 窗函数分析法（任何有限长度信号 = 无限长信号 × 窗函数）

  • 无限长复指数信号：$e^{j2\pi f_{k}t}$ → 频域是 冲激函数 $\delta (f-f_k)$

  • 矩形窗 ${\text{rect}}_T(t)$ → 频域是 $T\cdot \text{sinc}(fT)$

  • 时域相乘 → 频域卷积：
    F{ej2πfkt⋅rectT(t)}=δ(f−fk)∗[T⋅sinc(fT)]=T⋅sinc((f−fk)T)\mathcal{F}\{ e^{j2\pi f_k t} \cdot \text{rect}_T(t) \} = \delta(f - f_k) * \left[ T \cdot \text{sinc}(f T) \right] = T \cdot \text{sinc}\left( (f - f_k) T \right) F{ej2πfk​t⋅rectT​(t)}=δ(f−fk​)∗[T⋅sinc(fT)]=T⋅sinc((f−fk​)T)

  • 结论：频域是 Sinc 函数，中心在 $f_k$。使用Geogebra绘制：

S(x) = if(x ≠ f_k, sin(π * (x - f_k)) / (π * (x - f_k)), 1)

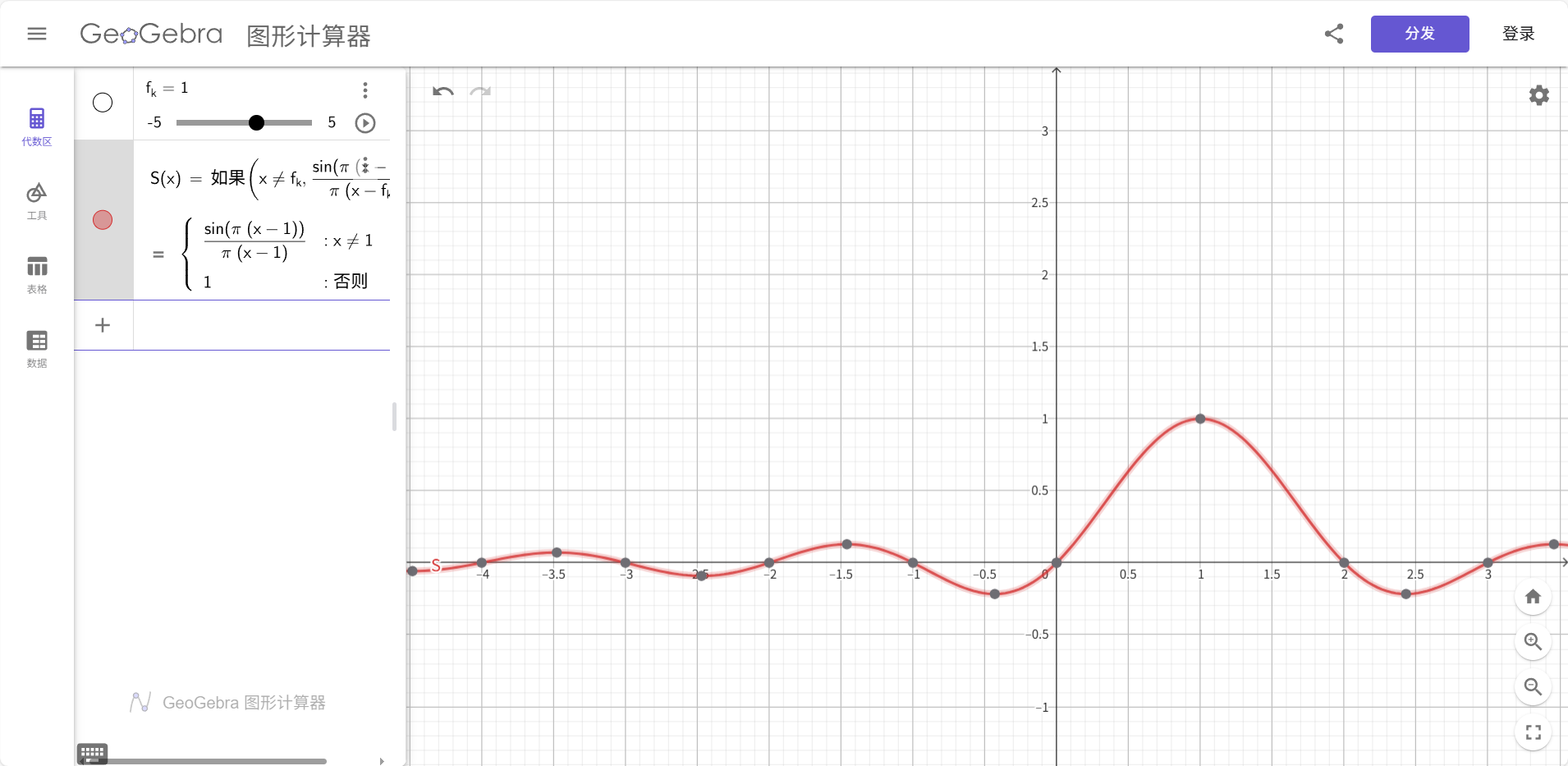
• 时域相乘 → 频域卷积
  • OFDM 子载波时域信号：$s_k(t)=e^{j2\pi f_{k}t}\cdot {\text{rect}}_T(t)$
  • 傅里叶变换的调制性质（或频移性质）：F{ej2πfktg(t)}=G(f−fk)\mathcal{F}\{ e^{j2\pi f_k t} g(t) \} = G(f - f_k)F{ej2πfk​tg(t)}=G(f−fk​)，其中 G(f)=F{g(t)}G(f) = \mathcal{F}\{g(t)\}G(f)=F{g(t)}
  • 令 $g(t)={\text{rect}}_T(t)$，其傅里叶变换为$G(f)=T\cdot \text{sinc}(fT)$
  • 所以：
    Sk(f)=F{ej2πfkt⋅rectT(t)}=T⋅sinc((f−fk)T)S_k(f) = \mathcal{F}\{ e^{j2\pi f_k t} \cdot \text{rect}_T(t) \} = T \cdot \text{sinc}\left( (f - f_k) T \right) Sk​(f)=F{ej2πfk​t⋅rectT​(t)}=T⋅sinc((f−fk​)T)

正交性反推法

• 使用有限时间的正弦波，导致 Sinc 频谱 → 为了实现正交性，必须重新考虑。

• 先考虑加窗正交的定义：两个信号 $s_k(t)$ 和 $s_m(t)$ 在区间 ([0, T]) 上正交，当且仅当（$s_m^{\ast }(t)$ 表示 $s_m(t)$ 的复共轭）：

$$⟨s_k,s_m⟩={\int }_0^T{s}_k(t)\cdot s_m^{\ast }(t)dt=0,\text{当 }k\ne m$$

• 设计一组正交的子载波，希望：
  $$\begin{gathered} {\int }_0^T{e}^{j2\pi f_{k}t}{e}^{-j2\pi f_{m}t}dt=0\text{当 }k\ne m \\ {\int }_0^T{e}^{j2\pi (f_k-f_m)t}dt=0 \end{gathered}$$

• 积分在 $f_k-f_m=n/T$（n 为整数）时为 0。
  $${\int }_0^T{e}^{j2\pi nt/T}dt={\left[\frac{e^{j2\pi nt/T}}{j2\pi n/T}\right]}_0^T=\frac{e^{j2\pi n}-1}{j2\pi n/T}$$

• 由于 $e^{j2\pi n}=\cos (2\pi n)+j\sin (2\pi n)=1+j0=1$：

$$=\frac{1-1}{j2\pi n/T}=0$$

• 所以，最自然的选择是：
  $$f_k=k/T$$

正交性结论

$$\boxed{{\int }_0^T{s}_k(t)s_m^{\ast }(t)dt=\{\begin{array}{ll}T,& k=m\\ 0,& k\ne m\end{array}}$$

接收端利用正交性解调

• 设发送信号为：

$$x(t)=\sum _{k=0}^{N-1}{a}_k{s}_k(t)=\sum _{k=0}^{N-1}{a}_k{e}^{j2\pi (k/T)t},0\le t<T$$

• 其中 $a_k$ 是第 $k$ 个子载波的调制符号（如 QPSK、16-QAM）。

• 接收端解调第 $m$ 个子载波：

$${\hat{a}}_m=\frac{1}{T}{\int }_0^{T}x(t)\cdot s_m^{\ast }(t)dt$$

• 代入 $x(t)$：

$${\hat{a}}_m=\frac{1}{T}{\int }_0^T\left(\sum _{k=0}^{N-1}{a}_k{s}_k(t)\right)s_m^{\ast }(t)dt=\frac{1}{T}\sum _{k=0}^{N-1}{a}_k\underset{=T\cdot {\delta }_{km}}{\underbrace{{\int }_0^T{s}_k(t)s_m^{\ast }(t)dt}}$$

• 其中 ${\delta }_{km}$ 是 Kronecker delta 函数：

$${\delta }_{km}=\{\begin{array}{ll}1,& k=m\\ 0,& k\ne m\end{array}$$

• 所以：

$${\hat{a}}_m=\frac{1}{T}\sum _{k=0}^{N-1}{a}_k\cdot T\cdot {\delta }_{km}=a_m$$

例子

参数	值	说明
符号周期 $T$	100 μs	不含循环前缀
子载波间隔 $\Delta f$	$\frac{1}{T}=10\text{kHz}$	正交性要求
函数	S1(x) = sin(π * (x - 10000)) / (π * (x - 10000)) ， S2(x) = sin(π * (x - 20000)) / (π * (x - 20000))， S3(x) = sin(π * (x - 30000)) / (π * (x - 30000))	好像geogebra会自动补充极限位置的值，所以不设置分段函数了

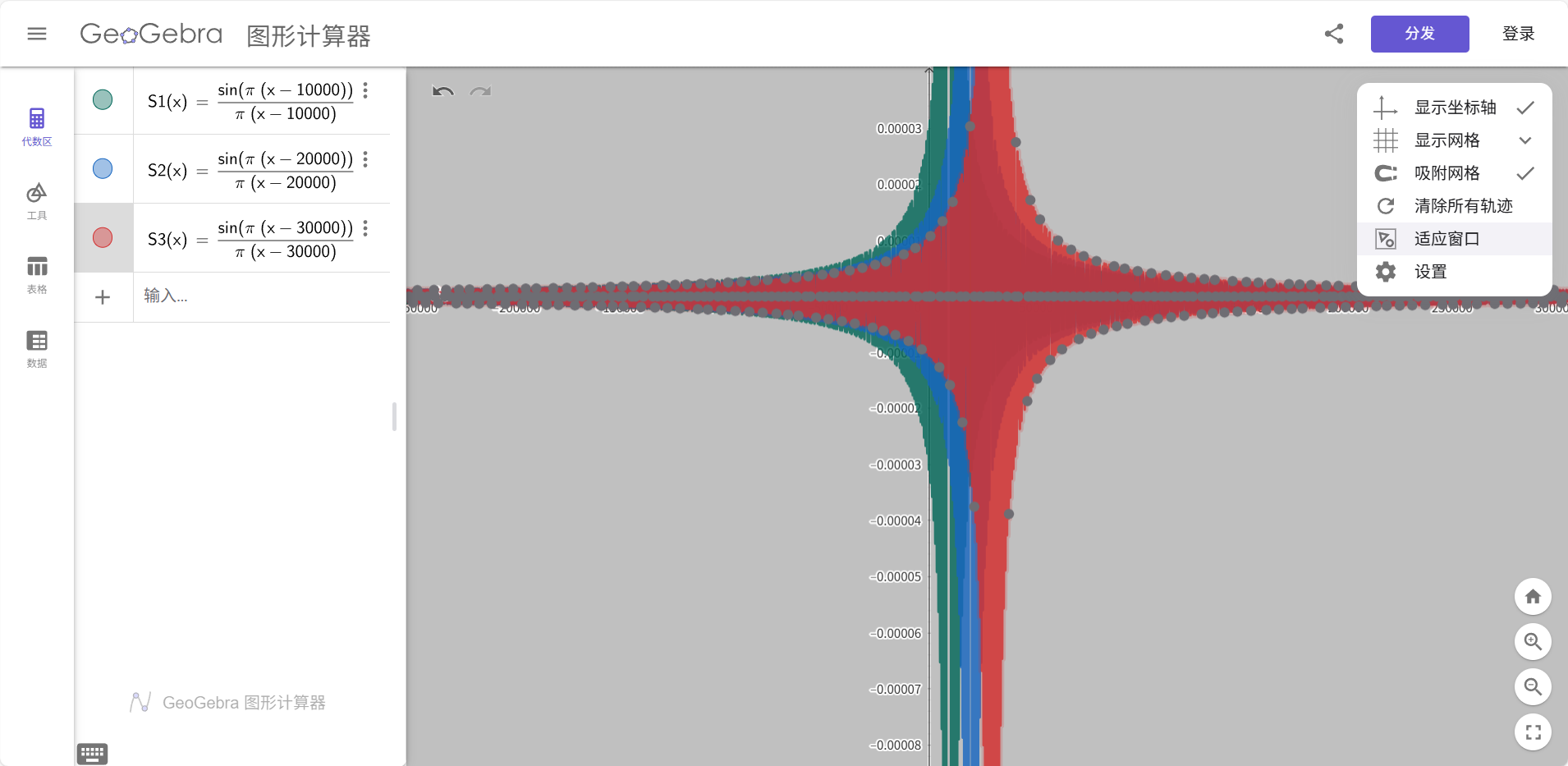
• 以上设置不方便geogebra绘图，为了方便观察，设置以下参数：

参数	值	说明
符号周期 $T$	1s	不含循环前缀
子载波间隔 $\Delta f$	$\frac{1}{T}=1\text{Hz}$	正交性要求
函数	S1(x) = sin(π * (x - 1)) / (π * (x - 1)) ， S2(x) = sin(π * (x - 2)) / (π * (x - 2))， S3(x) = sin(π * (x - 3)) / (π * (x - 3))	好像geogebra会自动补充极限位置的值，所以不设置分段函数了

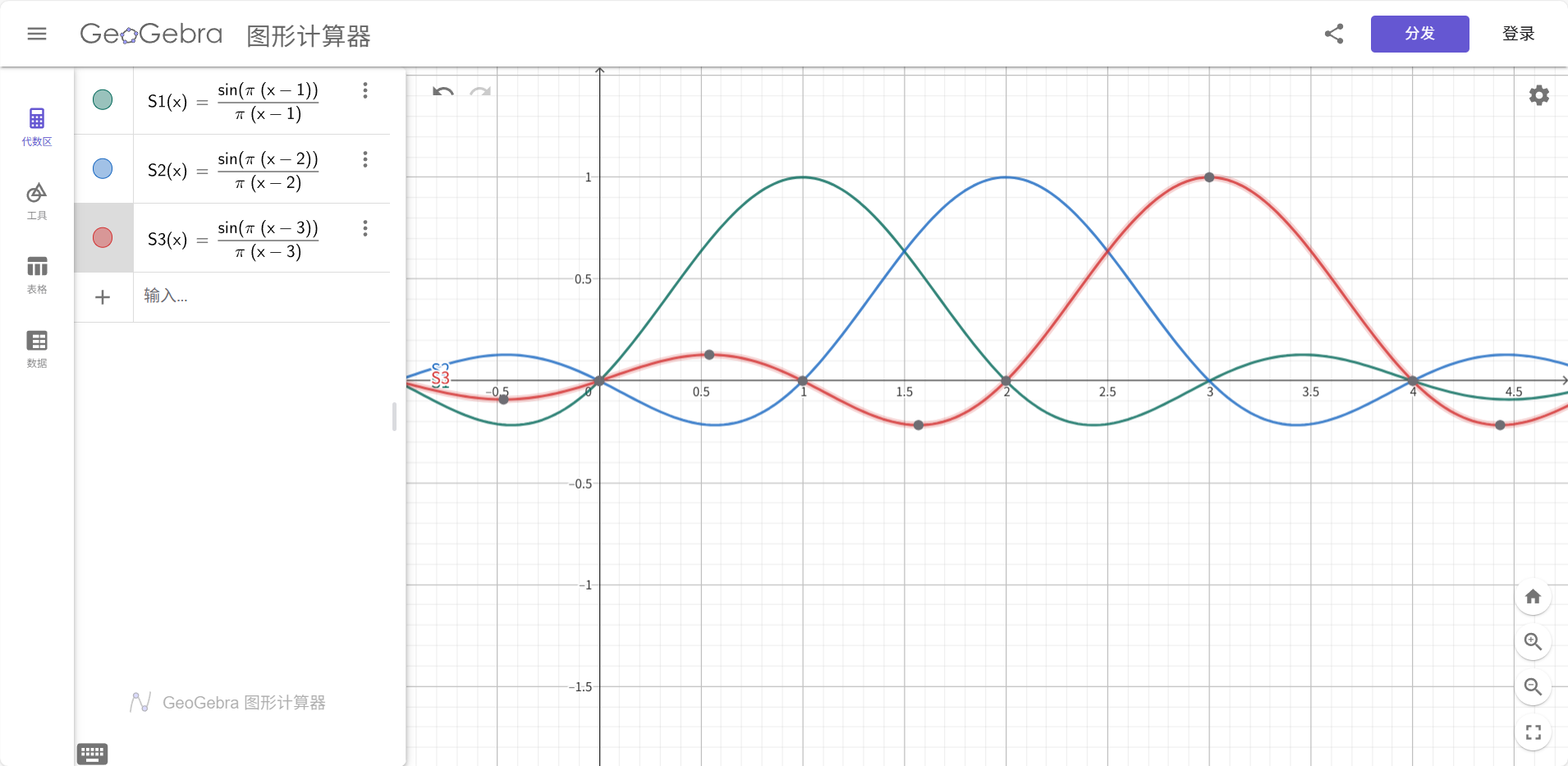
• 虽然子载波的 Sinc 频谱重叠，但在每个子载波的中心频率点，其他子载波的 Sinc 函数值恰好为 零，当接收机在 $f_m$ 处采样时，只“看到”第 $m$ 个子载波的峰值，其他子载波在此处无能量。