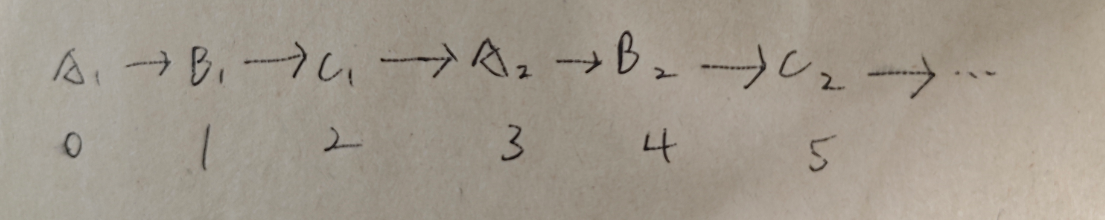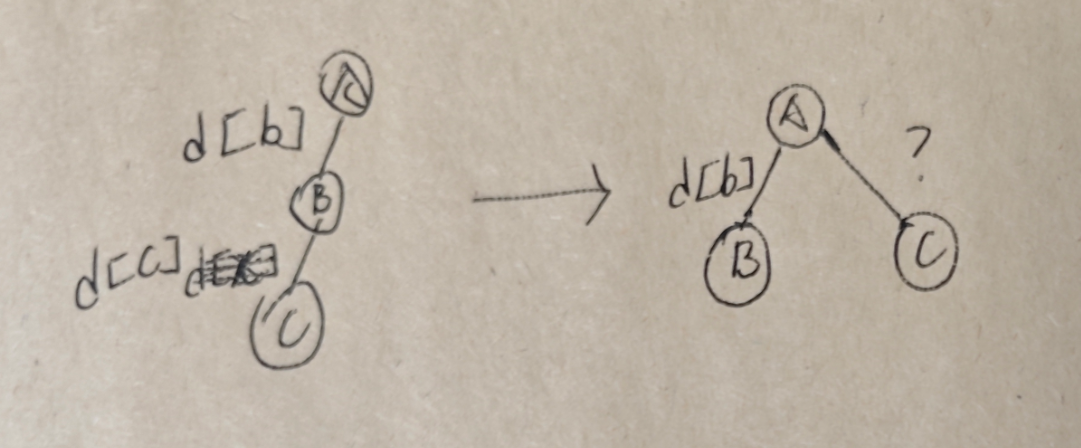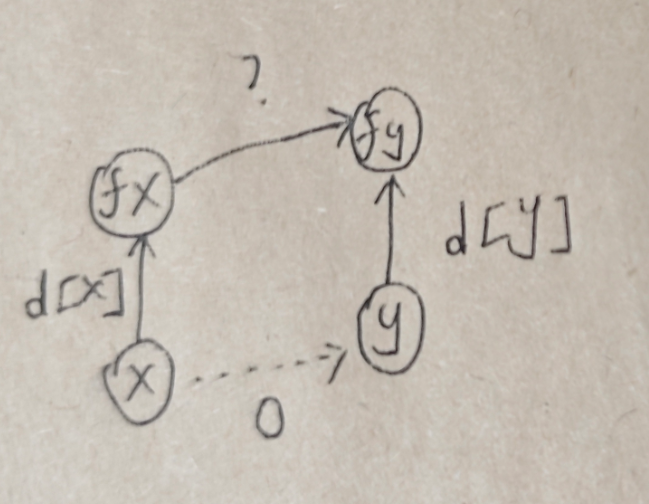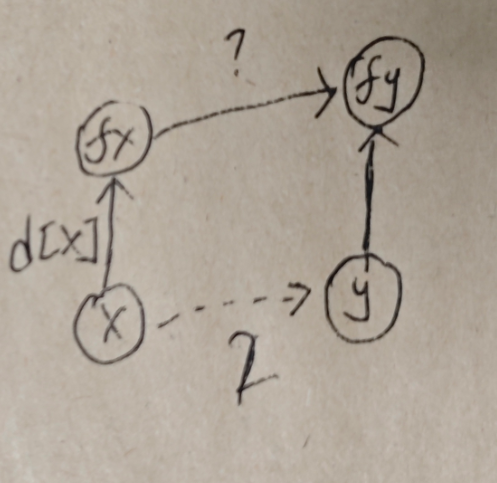算法题（190）：食物链（带权并查集）

审题：
本题需要我们通过维护食物链关系并判断给出的指令的真伪，将所有假指令的数目统计出来并输出

思路：

方法一：带权并查集

由于食物链的关系是A,B,C环形克制，其实存在一个周期循环。

我们依次给这些动物编号，可以总结出一个解决方法

首先我们看看同类动物之间的距离：3,6,9....

我们发现同类动物之间的距离都是3的倍数，取模3之后都是0

接着看看捕食关系的动物（x->y）：1,4,7...

x捕食y的距离都是取余3后值为1

最后看看被捕食关系的动物（y->x）：2,5,8...

值取余3后为2

综上，三种情况都可以通过两者之间的距离取余3的出的结果进行判断

我们将d[X]定义为x节点到根节点的距离，这个距离就是权值

---

接下来我们分析find函数的d数组数据如何更新

图示：

在路径压缩前，我们的c节点到a根节点之间的距离是d[c]+d[b]（b节点一定要先直接挂在根节点下）,路径压缩后的d[c]表示的就不是到b节点的距离，而是到根节点的距离，而由于c到a之间的距离从未变过，所以建立等式：d[c] = d[c] + d[b] =》 d[c]+=d[b]

---

然后是un函数

(1)指令为同类的情况

其中d[x]和d[y]都是已知的，然后由于同类之间的距离都是3的倍数，最终计算的时候利用了取余3，所以我们x和y的距离用取余3的结果代替也是可以的，所有3的倍数取余3都是0，所以让x和y的距离为0即可

等式：d[x] + d[xy] = d[y] + 0

(2)指令为捕食关系的情况

正常来说我们的捕食者和被捕食者之间的距离是1,4,7...但是如果我们用1当权值会导致计算公式不统一。而我们计算两者之间的距离可以用后者减前者，所以距离又可以是-1,2,5.此时我们可以用2来做权值，因为2和-1是同余的。这样就解决了用1当权值的问题

解题：

#include<iostream>
using namespace std;
const int N = 5e4 + 10;
int fa[N],d[N];
int n, k,ret = 0;
int find(int x)
{if (fa[x] == x) return x;int t = find(fa[x]);//一定要先执行此语句，先将父节点都挂在根节点处d[x] += d[fa[x]];//分析而得return fa[x] = t;
}
void un(int x, int y, int num)
{int a = find(x);int b = find(y);if (a != b){fa[a] = b;d[a] = d[y] + num - d[x];//不可以用d[fa[x]]应为此时fa[x]已经是等于b了}
}
int main()
{cin >> n >> k;//初始化for (int i = 1; i <= n; i++) fa[i] = i;while (k--){int op, x, y;cin >> op >> x >> y;if (x > n || y > n){ret++;continue;}if (op == 1)//同类{if (find(x) == find(y) && ((d[y] - d[x]) % 3 + 3) % 3 != 0){ret++;}else un(x, y, 0);}else//x->y{if (find(x) == find(y) && ((d[y] - d[x]) % 3 + 3) % 3 != 1){ret++;}else un(x, y, 2);}}cout << ret << endl;return 0;
}

注意：
1.在un函数中，需要特别注意我们不能写成：d[fa[x]] = d[y] + num - d[x]

因为我们需要求的d是原来x的根节点a的d，此时fa[x]已经更新为b了，也就是说此时d[fa[x]]==d[b]

2.指令为同类时的更新前提：当前的x和y之间存在关系且不为同类情况

指令为x捕食y时的更新前提：当前的x和y之间存在关系且不为x捕食y的情况

3.为了方便x捕食y情况的代码统一性，我们采用后者减前者的方式计算两者间距离

4.由于我们不确定谁距离根节点更近，所以结果可能会出现负数取余，此时我们就要使用“模加模”的方法来解决负数取模问题

P2024 [NOI2001] 食物链 - 洛谷