当前位置：首页 > news >正文

梯度提升决策树（GBDT）：从原理到实战，掌握结构化数据建模的核心利器

news 2025/8/21 6:58:21

在机器学习领域，梯度提升决策树（GBDT）堪称经典。

它凭借高效捕捉复杂模式的能力，成为Kaggle竞赛和工业界的常青树。

作为一名长期实践者，我认为深入理解GBDT不仅是技术必修课，更能提升数据建模的实战能力。

本文将从Boosting思想的起源讲起，逐步解析梯度提升的数学本质，并通过Python案例演示全流程。无论您是初学者还是资深从业者，都能从中获益——我们不仅“知其然”，更要“知其所以然”，最终实现从理论到落地的平滑过渡。

一、从Boosting到梯度提升：弱模型的智慧组合

1.1 Boosting：突破性能边界的巧思

在传统机器学习中，集成学习通过组合多个模型提升效果，主要分两类：

Bagging类算法（如随机森林），通过自助采样训练独立子模型，再投票或平均结果。
Boosting类算法（如AdaBoost或GBDT），通过迭代训练让新模型修正前序错误，逐步逼近目标。

Boosting的核心在于：弱模型（仅略优于随机猜测）的有序组合，能逼近强模型性能。早期代表AdaBoost通过调整样本权重间接优化损失，但缺乏明确的数学目标。直到1999年，Jerome Friedman提出梯度提升（Gradient Boosting），首次将梯度下降思想引入集成学习，为Boosting奠定了优化框架。

1.2 梯度提升：函数空间的梯度下降

梯度提升的本质，是在函数空间中沿负梯度方向迭代，逐步逼近损失函数的最小值。这一过程类似“模型空间的精准滑坡”，每一步都力求更优。

数学推导的关键步骤如下：

假设目标函数是 F(x)，需最小化损失函数 L(y,F(x))，流程可形式化为：

初始化：选择基础函数 F0(x)，例如回归任务中设为标签均值 F0(x)=yˉ。
迭代优化（第m轮）：
a. 计算负梯度（伪残差）：
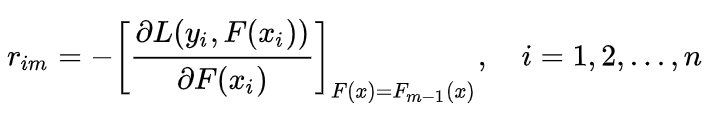
b. 用基学习器拟合伪残差：训练决策树 hm(x)拟合伪残差 rim。
c. 确定最优步长：通过线搜索计算步长 γm，使损失最小化：
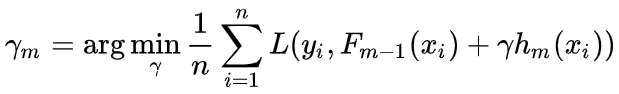
d. 更新模型： Fm(x)=Fm−1(x)+ν⋅γmhm(x)，其中 ν为学习率（控制步长，防震荡）。

简言之，每棵新树都在当前模型的“最陡下降方向”上寻求增量改进，而学习率则像“刹车踏板”，确保优化稳定。

二、GBDT核心原理：适配不同任务的损失函数

2.1 回归任务：MSE损失下的残差拟合

回归任务常用均方误差（MSE）作为损失函数： L(y,F)=21(y−F)2。此时，负梯度简化为残差 ri=yi−F(xi)。因此，GBDT每棵树直接拟合当前残差，逐步累加修正值。

示例：假设真实值 y=10，初始模型预测为5（残差5）。第一棵树拟合残差后，若学习率0.1，模型更新为5 + 0.1×5 = 5.5；第二棵树拟合新残差4.5，依此类推直至收敛。这一过程直观且高效。

2.2 分类任务：对数损失与概率校准

分类任务常用对数损失（Log Loss）函数：

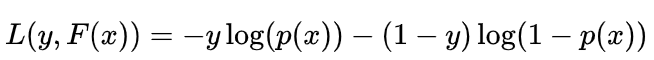
其中 p是sigmoid函数输出的正类概率。此时，负梯度为：

ri=yi−pi

多分类任务中，GBDT使用多项对数损失，每类对应一个子模型，通过Softmax输出概率，负梯度类似指示函数调整。这确保了概率预测的校准性。

三、GBDT实战全流程：代码与工程细节解析

3.1 案例：房价预测（回归任务）

使用scikit-learn的California房价数据集，演示回归建模。

环境准备：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, r2_score# 加载数据
data = fetch_california_housing()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"训练集样本数: {X_train.shape[0]}, 测试集样本数: {X_test.shape[0]}")

基础模型训练：

gbdt_reg = GradientBoostingRegressor(random_state=42)
gbdt_reg.fit(X_train, y_train)
y_pred = gbdt_reg.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"MSE: {mse:.4f}, R²: {r2:.4f}")  # 输出评估结果

残差分析与特征重要性：
可视化残差图可诊断模型偏差，特征重要性图则揭示关键因子（代码略，详见原文）。我们建议优先关注特征重要性，指导特征工程。

3.2 案例：信用卡违约预测（分类任务）

使用Kaggle数据集演示分类任务（数据预处理代码略）。

基础模型训练：

gbdt_clf = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
gbdt_clf.fit(X_train, y_train)
y_pred = gbdt_clf.predict(X_test)
print(classification_report(y_test, y_pred))  # 输出分类报告

参数调优：早停法与网格搜索：
早停法（n_iter_no_change=50）可防过拟合，网格搜索则优化超参数（如学习率、树深度）。实践中，我们建议先调学习率和树数量，再调整其他参数。

四、GBDT与其他集成算法的对比

算法	基学习器	学习方式	优势	适用场景
GBDT	CART回归树	串行	理论严谨，梯度优化保证收敛	小数据精细调优
AdaBoost	任意弱分类器	串行	实现简单，无需调整损失函数	二分类任务
随机森林	CART决策树	并行	抗过拟合强，训练效率高	大规模数据快速建模
XGBoost	CART回归树	串行	支持正则化和并行计算	工业级大数据场景