动态规划:入门思考篇
1. 简单类比
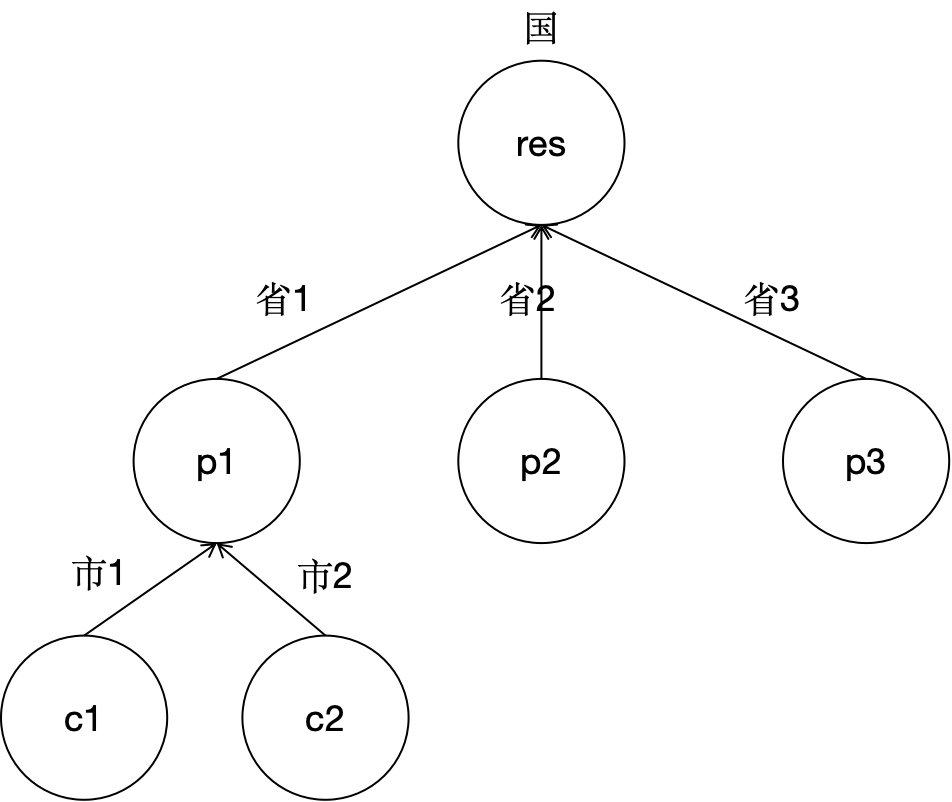
假如我们要求全国人数,那么我们只要知道各个省的人数,然后将各个省的人数相加即可,要想知道各个省的人数,只要将这个省下面所有的市人数相加即可,同样,如果想要知道各个市的人数,只要知道下面所有县的人数即可。
这就是动态规划的核心思想:将原问题拆解为更小的子问题,求解每个子问题的最优解后,通过组合子问题的解得到原问题的解
| 类比逻辑 | 动态规划核心概念 | 关键说明 |
|---|---|---|
| 全国人数(最终目标) | 原问题(Original Problem) | 需要求解的最终复杂问题。 |
| 省 / 市 / 县人数 | 子问题(Subproblems) | 原问题拆解出的、规模更小的同类问题(子问题需与原问题 “同结构”,如都是 “统计某区域人数”)。 |
| 省 = 市相加 / 市 = 县相加 | 状态转移方程(State Transition) | 子问题的解如何组合成父问题的解(你的例子中是 “求和”,DP 中可能是 “取最大 / 最小 / 累加” 等)。 |
| 县人数(最底层) | 边界条件(Base Case) | 无需再拆解的最小子问题,有直接已知的解(如 “某县人数 = 统计局直接公布的数据”,无需再拆到乡镇)。 |
2. “分治” 与 “最优子结构”
如果我们有很多种解决方案,但是我们想要找出最优的方案。一种方法就是,我们将所有的方案划分成不同的集合,这些集合之间互不重叠,结合内部也没有重合的方案,此时我们只要求解出各个集合的最优方案,然后从最优方案中选出最优即可。
要确保通过 “划分集合→找集合最优→选最终最优” 能得到全局最优解,需满足以下两点,这是避免 “漏掉最优方案” 或 “选不出真最优” 的核心:
- 前提 1:集合的 “完全覆盖性”
划分的所有集合必须覆盖全部可能的解决方案,不能有遗漏。
例如:若要选 “从家到公司的最优路线”,若只划分 “走地铁” 和 “骑自行车” 的集合,却漏掉 “坐公交” 的集合,可能恰好 “坐公交” 是耗时最短的最优方案,最终结果就会出错。 - 前提 2:“最优子结构” 成立
每个集合的 “局部最优方案”,必须是支撑 “全局最优方案” 的候选。换句话说,全局最优方案一定来自某个集合的局部最优方案,不会存在 “某个集合的非最优方案,比所有集合的最优方案更好” 的情况。
例如:若划分 “从家到公司走东边” 和 “走西边” 两个集合,若 “东边集合的最优路线(20 分钟)” 和 “西边集合的最优路线(25 分钟)”,则全局最优一定是东边的 20 分钟,不会存在 “东边集合里某条 22 分钟的路线,比西边最优还快” 的矛盾 —— 这就是最优子结构的体现。
| 你的通用框架 | 动态规划(DP)的补充细节 | 贪心算法的补充细节 |
|---|---|---|
| 划分互不重叠的方案集合 | 划分的 “集合” 对应 “子问题”,且子问题存在重叠性(需存储解避免重复计算) | 划分的 “集合” 对应 “每一步的选择”,且需满足贪心选择性质(每步选局部最优就能推全局最优) |
| 求每个集合的最优方案 | 通过 “状态转移方程” 计算子问题最优解(依赖更小的子问题) | 直接选择当前集合的 “局部最优”(无需依赖后续子问题,一步到位) |
| 从局部最优中选全局最优 | 最终问题的解就是最顶层子问题的最优解 | 所有步骤的局部最优累加 / 组合,直接得到全局最优 |
3. 青蛙跳台阶
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
我们想要知道n阶的方案数,只要知道n-1阶的方案数和n-2阶的方案数即可。假如n=5
- 跳到第4阶的方案集合
1->2->3->4->5 1->2->4->5 2->4->5 2->3->4->5 - 跳到第3阶的方案集合
1->2->3->5 2->3->5 1->3->5
总之要想跳到第5阶,那么一定是从第3阶或者第4阶过来的,方案数也就是这两种集合方案数的和。我不知道跳到第4的阶的方案是什么,也不知道跳到第3阶的方案是什么,但是按照第3阶和第4阶,我可以将跳到第5阶所有的方案分成不重合的两个集合,只要求出这两个集合的方案数,然后相加就是最后的方案数。
这两个集合把所有的方案不重不漏的划分开来,符合无重叠性和完全覆盖性。第一个集合的所有方案,最后一步必然经过第4阶台阶,第二个集合的所有方案,最后一步必然经过第3阶台阶。
4. 集合的唯一划分标准
这里有一个困惑,集合一中不是也会有方案经过3吗,为什么不会与集合二重叠呢?
两个集合的划分标准是 “最后一步的来源”,而非 “方案是否经过某个中间台阶”,因此即使集合一的方案经过 3 阶,也不会与集合二重叠
- 集合一(来自 n-1 阶):所有方案的最后一步是 “从第 4 阶跳 1 阶到第 5 阶”(无论这个方案在到达 4 阶之前,是否经过 3 阶、2 阶等)。
例:方案 “1→2→3→4→5”,最后一步是 “4→5”,属于集合一;哪怕方案是 “1→3→4→5”,最后一步仍是 “4→5”,也属于集合一。 - 集合二(来自 n-2 阶):所有方案的最后一步是 “从第 3 阶跳 2 阶到第 5 阶”(无论这个方案在到达 3 阶之前,是否经过 2 阶、1 阶等)。
例:方案 “1→2→3→5”,最后一步是 “3→5”,属于集合二;哪怕方案是 “1→3→5”,最后一步仍是 “3→5”,也属于集合二。
一个方案的 “最后一步” 是唯一的、不可拆分的,这是避免重叠的核心:
- 集合一的方案,无论中间是否经过 3 阶,其 “最后一步” 必然是 “4→5”(跳 1 阶);
- 集合二的方案,无论中间是否经过其他台阶,其 “最后一步” 必然是 “3→5”(跳 2 阶)。
这就像 “无论你之前走了哪条路,最后一步是‘迈左脚进门’还是‘迈右脚进门’,是完全不同的两个动作”—— 不会存在一个方案,“最后一步既从 4 阶跳 1 阶,又从 3 阶跳 2 阶”,因此两个集合绝对无重叠。
5. 01背包问题
有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
比如有3个物品,a,b,c,d每个物品的价值为10, 15,20,30,重量分别为1,2,2,3,背包的重量为4
我们有2N2^N2N中选择,也就有2N2^N2N中方案,我们从这些方案中选择一个最优的方案,能装下的价值最大。
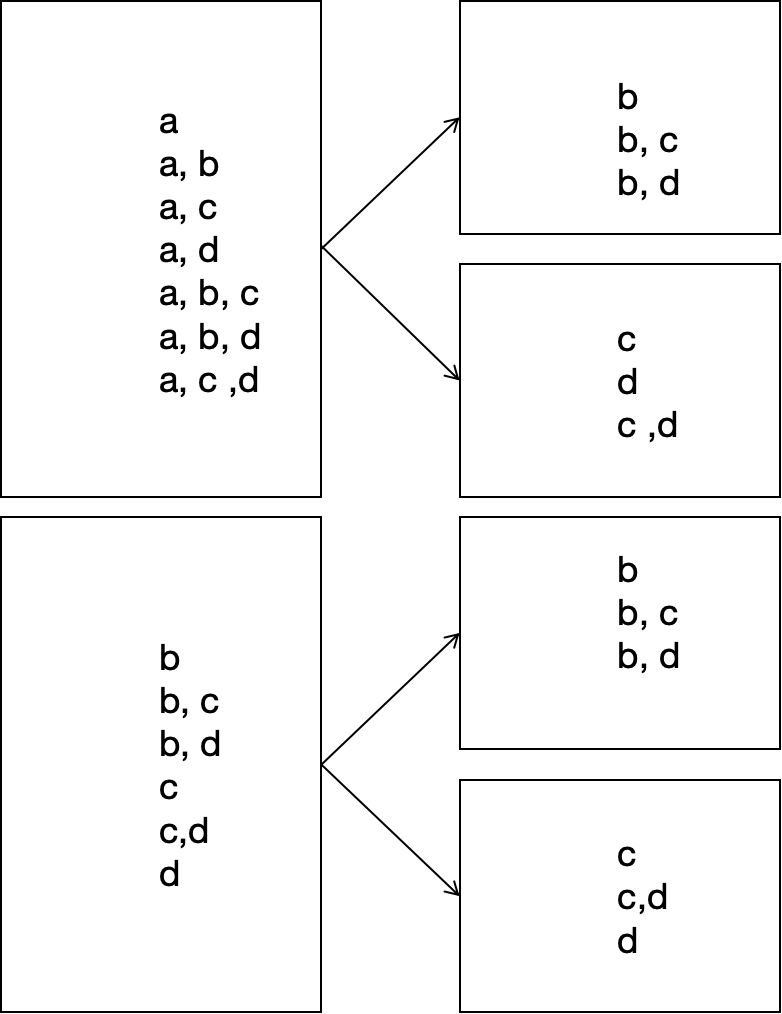
如果我们能将所有的方案分组,然后获取每个组内的最大价值,那么最大的那个价值就是最终的价值。一种简单的划分就是我们是否选择某个物品,例如我们是否选择a
- 选择a的方案
a a, b a, c a, d a, b, c a, b, d a, c ,d - 不选择a的方案
b b, c b, d c c,d d
可以看到两种方案完全没有重合,因为集合一全部的方案都包含a,集合二所有的方案都不包含a,通过这种集合划分方式,我们得到了所有的方案,并且两个集合中没有重复的方案。对于集合一和集合二,我们可以再次通过是否选择b划分为更小的集合。
子问题重叠
你的类比中,子问题(省、市、县)是 “互不重叠” 的(一个县只属于一个市,一个市只属于一个省),而动态规划的典型场景中,子问题往往是 “重叠” 的(即不同父问题可能依赖同一个子问题的解)。
