Python-深度学习.pytorch（二）——自动微分、认识深度学习

目录

一、自动微分概念

1、张量

2、计算题

3、反向传播

4、梯度

二、梯度计算

1、标量梯度计算

2、向量梯度计算

三、梯度控制

1、控制梯度计算

2、累计梯度

3、梯度清零

案例

---

        自动微分模块torch.autograd负责自动计算张量操作的梯度，具有自动求导功能。自动微分模块是构成神经网络训练的必要模块，可以实现网络权重参数的更新，使得反向传播算法的实现变得简单而高效

（梯度运算必须是浮点型（float））

一、自动微分概念

        1、张量

        torch中一切皆为张量，张量的属性requires_grad决定是否对其进行梯度计算。默认是 False，如需计算梯度则设置为True

        2、计算题

        torch.autograd通过创建一个动态计算图来跟踪张量的操作，每个张量是计算图中的一个节点，节点之间的操作构成图的边

        在 PyTorch 中，当张量的 requires_grad=True 时，PyTorch 会自动跟踪与该张量相关的所有操作，并构建计算图。每个操作都会生成一个新的张量，并记录其依赖关系。表示该张量在计算图中需要参与梯度计算，即在反向传播（Backpropagation）过程中会自动计算其梯度

        当张量的 requires_grad= False 时，不会计算梯度

        叶子节点：

           在 PyTorch 的自动微分机制中，叶子节点（leaf node） 是计算图中，由用户直接创建的张量，它的 requires_grad=True，这些张量是计算图的起始点，通常作为模型参数或输入变量

（如果参与了计算，其梯度会存储在 leaf_tensor.grad 中 ，默认情况下，叶子节点的梯度不会自动清零，需要显式调用 optimizer.zero_grad() 或 x.grad.zero_() 清除 ）

特性	叶子节点	非叶子节点
创建方式	用户直接创建的张量	通过其他张量的运算生成
is_leaf 属性	True	False
梯度存储	梯度存储在 .grad 属性中	梯度不会存储在 .grad，只能通过反向传播传递
是否参与计算图	是计算图的起点	是计算图的中间或终点
删除条件	默认不会被删除	在反向传播后，默认被释放（除非 retain_graph=True）

通过 tensor.is_leaf 属性，可以判断一个张量是否是叶子节点

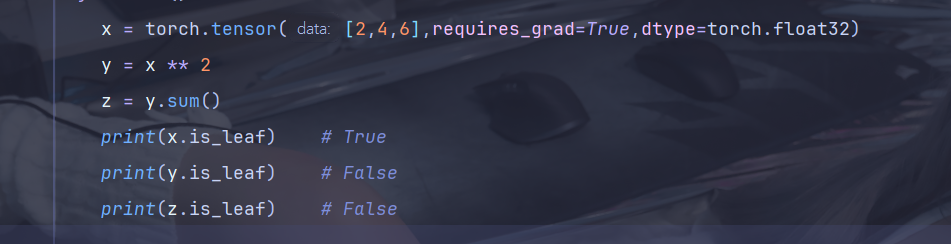
        3、反向传播

        使用tensor.backward()方法执行反向传播，从而计算张量的梯度。这个过程会自动计算每个张量对损失函数的梯度。

        4、梯度

        计算得到的梯度通过tensor.grad访问，这些梯度用于优化模型参数，以最小化损失函数

二、梯度计算

        1、标量梯度计算

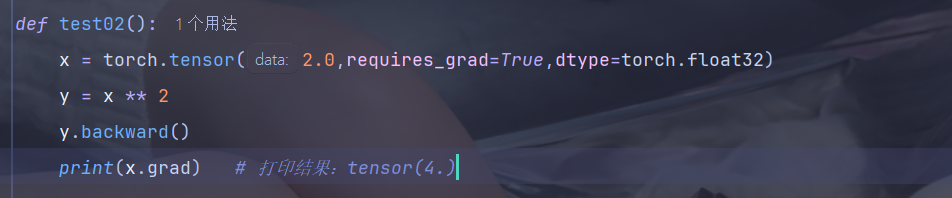
        2、向量梯度计算

        由于 y 是一个向量，我们需要提供一个与 y 形状相同的向量作为 backward() 的参数，这个参数通常被称为 梯度张量，它表示 y 中每个元素的梯度（这种方法使用较少，更常用下面的方法）

        我们也可以将向量 y 通过一个标量损失函数（如 y.mean()）转换为一个标量，反向传播时就不需要提供额外的梯度向量参数了。这是因为标量的梯度是明确的，直接调用 .backward() 即可

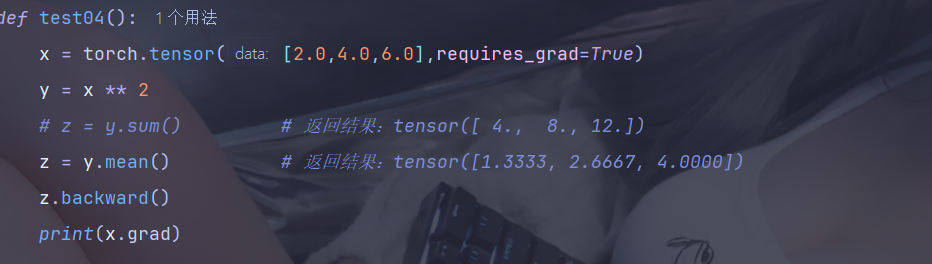
三、梯度控制

        1、控制梯度计算

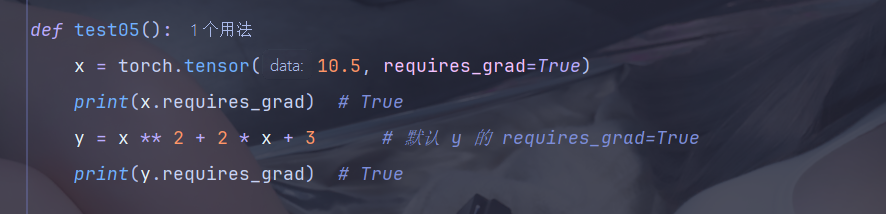
        可见，在这里，y 是会参与梯度计算的，而梯度计算是有性能开销的，有些时候我们只是简单的运算，并不需要梯度，此时可以通过使用 with、使用装饰器和全局设置来禁止 y 计算梯度

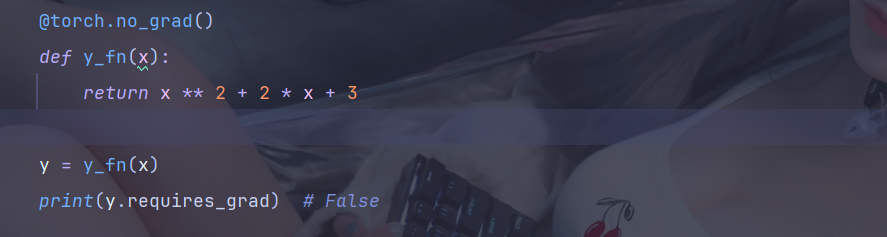
通常使用with方法最多，使用全局设置时一定要慎重

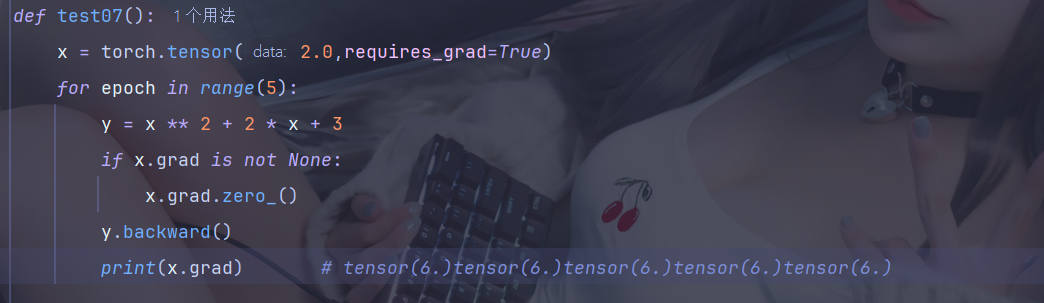
        2、累计梯度

        默认情况下，当我们重复对一个自变量进行梯度计算时，梯度是累加的

        3、梯度清零

        大多数情况下是不需要梯度累加的，因此就需要将梯度清零

        梯度清零要放在反向传播之前，因为 PyTorch 在计算梯度时采用的是“累加”模式，而不是“覆盖”模式，在 backward 中梯度计算公式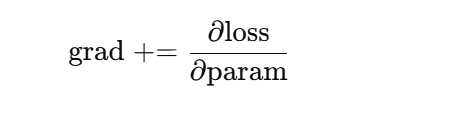：，所以清零要在运算前

案例

import torch# 定义随机数种子
torch.manual_seed(21)
# 定义两个随机数据
x = torch.randint(1,5,(1,20), dtype=torch.float)
y = torch.randint(1,5,(1,20), dtype=torch.float)
# 定义两个参数
a = torch.tensor(1,requires_grad=True,dtype=torch.float)
b = torch.tensor(2,requires_grad=True,dtype=torch.float)epochs = 51
# 学习率
lr = 0.01for epoch in range(1,epochs):# 前向传播 计算y的预测值y_predicted = a * x + b# 损失函数loss = ((y - y_predicted) ** 2).mean()# 梯度清零if (a.grad and b.grad) is not None:a.grad.zero_()b.grad.zero_()# 反向传播 计算梯度loss.backward()# 梯度下降with torch.no_grad():a -= lr * a.gradb -= lr * b.gradprint(f"epoch: {epoch}, loss: {loss}")
print(f"a: {a.grad}, b: {b.grad}")

掌握以上 tensor 和梯度的知识以后，将正式开始对深度学习的学习