机器学习之 KNN 算法学习总结
一、学习内容
今天的学习围绕机器学习中的 K 近邻算法(KNN)展开,通过理论讲解、案例分析和实践操作,系统掌握了 KNN 算法的原理、应用及实现过程。学习内容涵盖 KNN 算法的核心思想、距离度量方法、模型训练与评估流程,并结合电影分类、鸢尾花分类等实例进行了深入理解。
二、核心知识点梳理
(一)K 近邻算法(KNN)基础
- 算法定义:K 近邻算法(k-Nearest Neighbor)是一种基于实例的监督学习算法,核心思想是每个样本可以用其最接近的 K 个邻近值来代表。
- 核心原理:对于输入的无标签新数据,通过与样本集中数据的特征比较,提取最相似的 K 个数据的分类标签,最终选择这 K 个数据中出现次数最多的分类作为新数据的分类。
- 算法步骤:
- 计算已知类别数据集与当前点之间的距离
- 按照距离递增次序排序
- 选取与当前点距离最小的 K 个点
- 确定前 K 个点所在类别的出现频率
- 返回前 K 个点出现频率最高的类别作为当前点的预测分类
(二)距离度量方法
- 欧式距离:最常见的距离度量方式,衡量多维空间中两个点之间的绝对距离。
- 二维空间公式:d=(x1−x2)2+(y1−y2)2
- 三维空间公式:d=(x1−x2)2+(y1−y2)2+(z1−z2)2
- n 维空间公式:d=∑i=1n(xi−yi)2
- 曼哈顿距离:由赫尔曼・闵可夫斯基提出,指两个点在标准坐标系上的绝对轴距总和。平面上两点(x1,y1)与(x2,y2)的曼哈顿距离公式为:d(i,j)=∣x1−x2∣+∣y1−y2∣
(三)K 值的选择
- K 值是 KNN 算法的关键超参数,一般不大于 20。
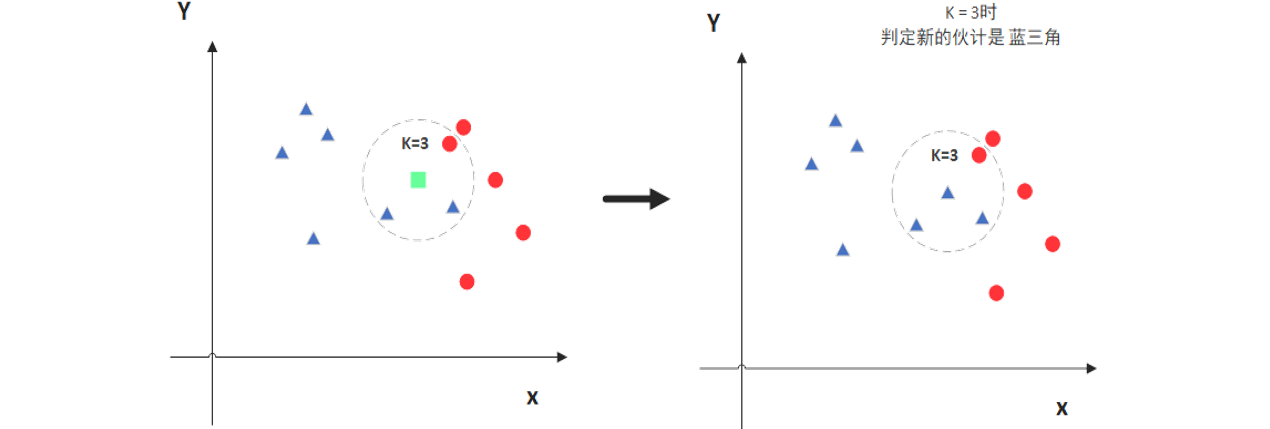
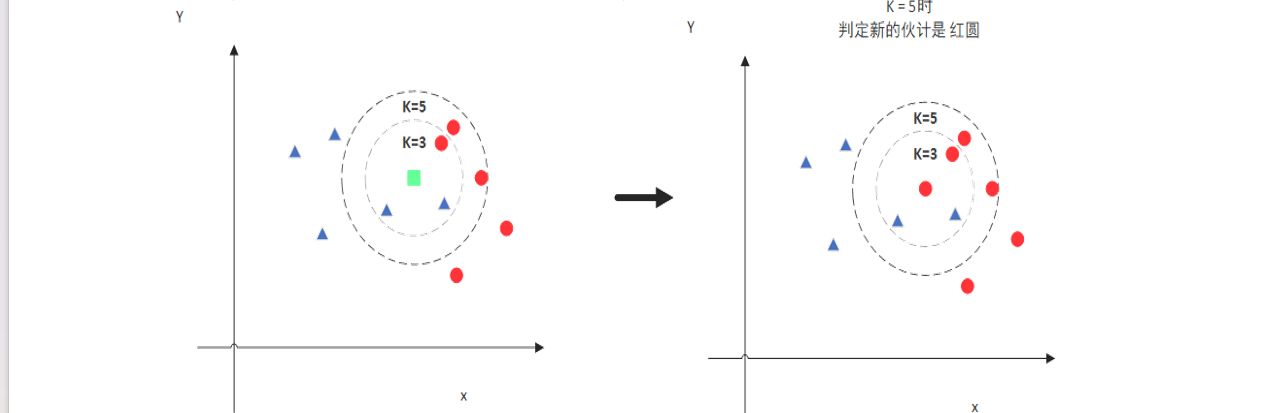
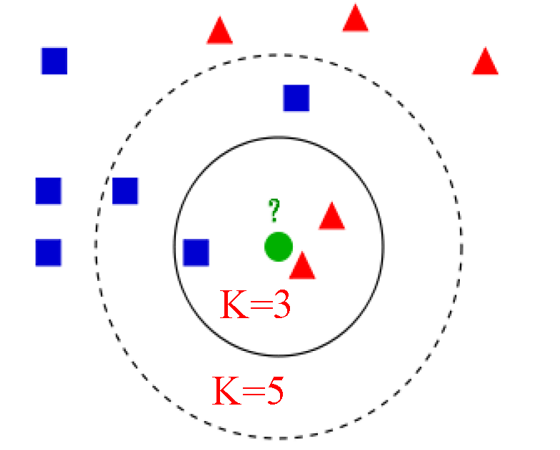
- K 值的选择会影响模型结果:K=3 时可能将新样本判定为某一类别,K=5 时可能因纳入更多邻近点而判定为另一类别。
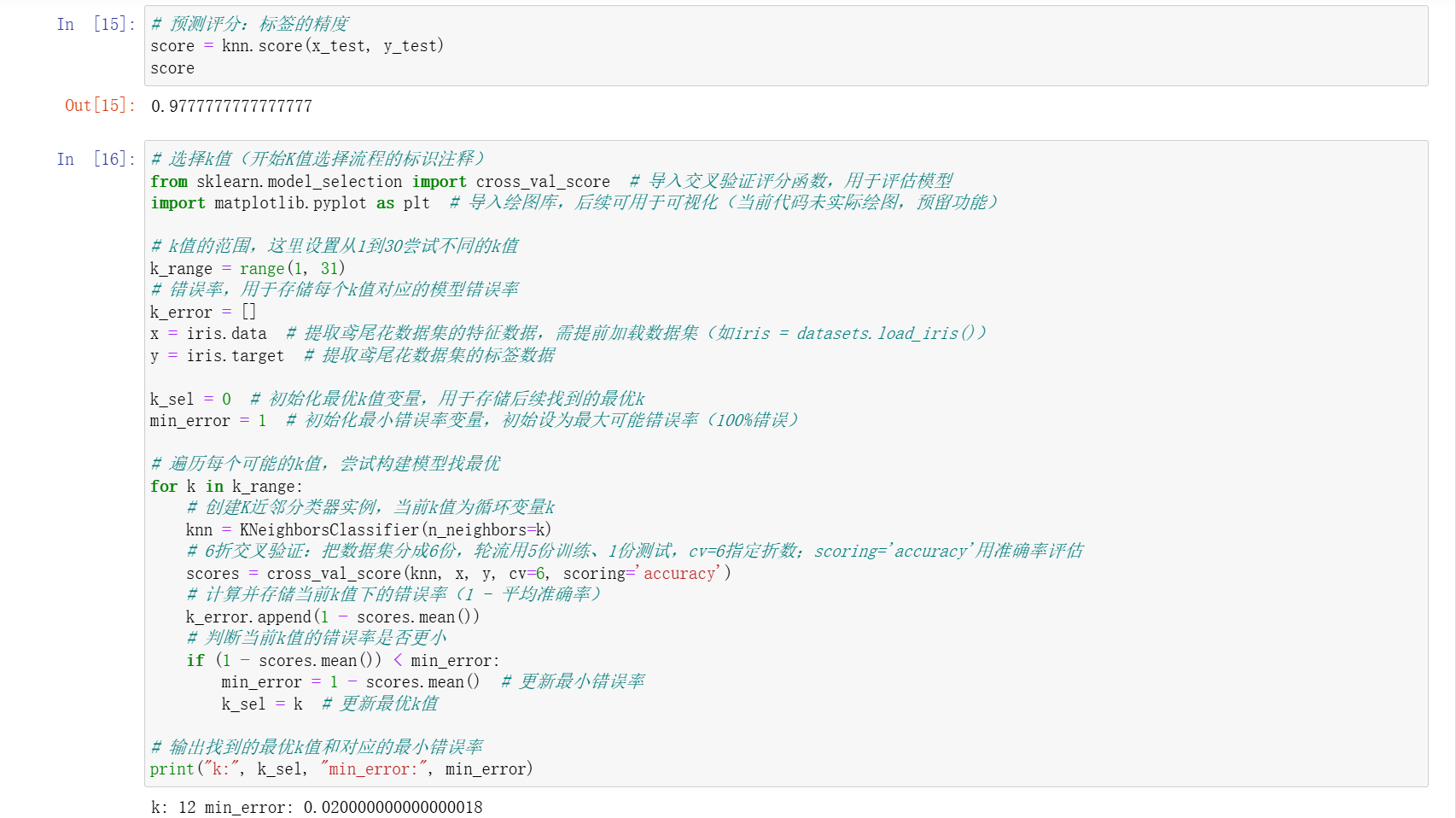
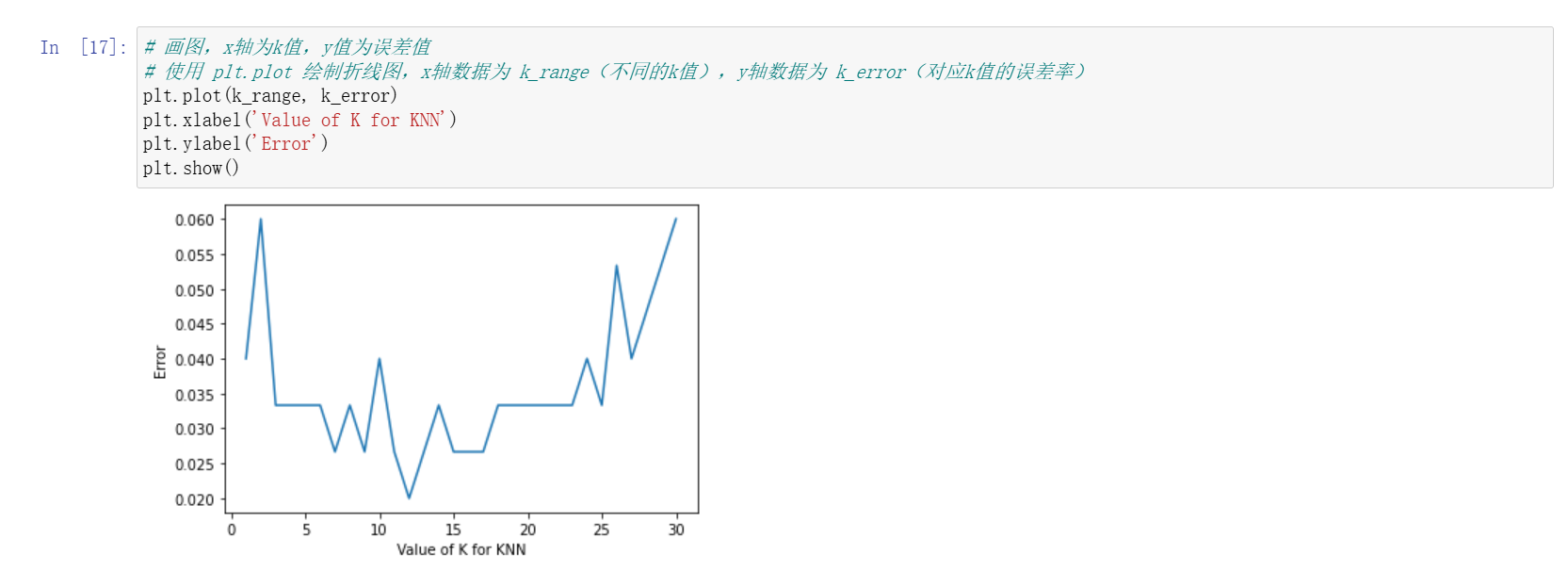
- 可通过交叉验证的方式选择最优 K 值,计算不同 K 值对应的错误率,选取错误率最小的 K 值作为最优参数。
三、实践案例
(一)电影分类案例
- 问题背景:根据电影中打斗镜头和接吻镜头的数量,判断电影属于爱情片还是动作片。已知部分电影的类别及特征数据,需确定未知电影(打斗镜头 18 次,接吻镜头 90 次)的类型。
- 数据示例:
- 爱情片:California Man(打斗 3 次,接吻 104 次)、He's Not Really into Dudes(打斗 2 次,接吻 100 次)等
- 动作片:Kevin Longblade(打斗 101 次,接吻 5 次)、Robo Slayer 3000(打斗 99 次,接吻 2 次)等
- 解决思路:通过计算未知电影与已知电影的距离(如欧式距离或曼哈顿距离),选取 K 个最近邻的电影类别,根据多数类判断未知电影类型。
(二)鸢尾花分类案例
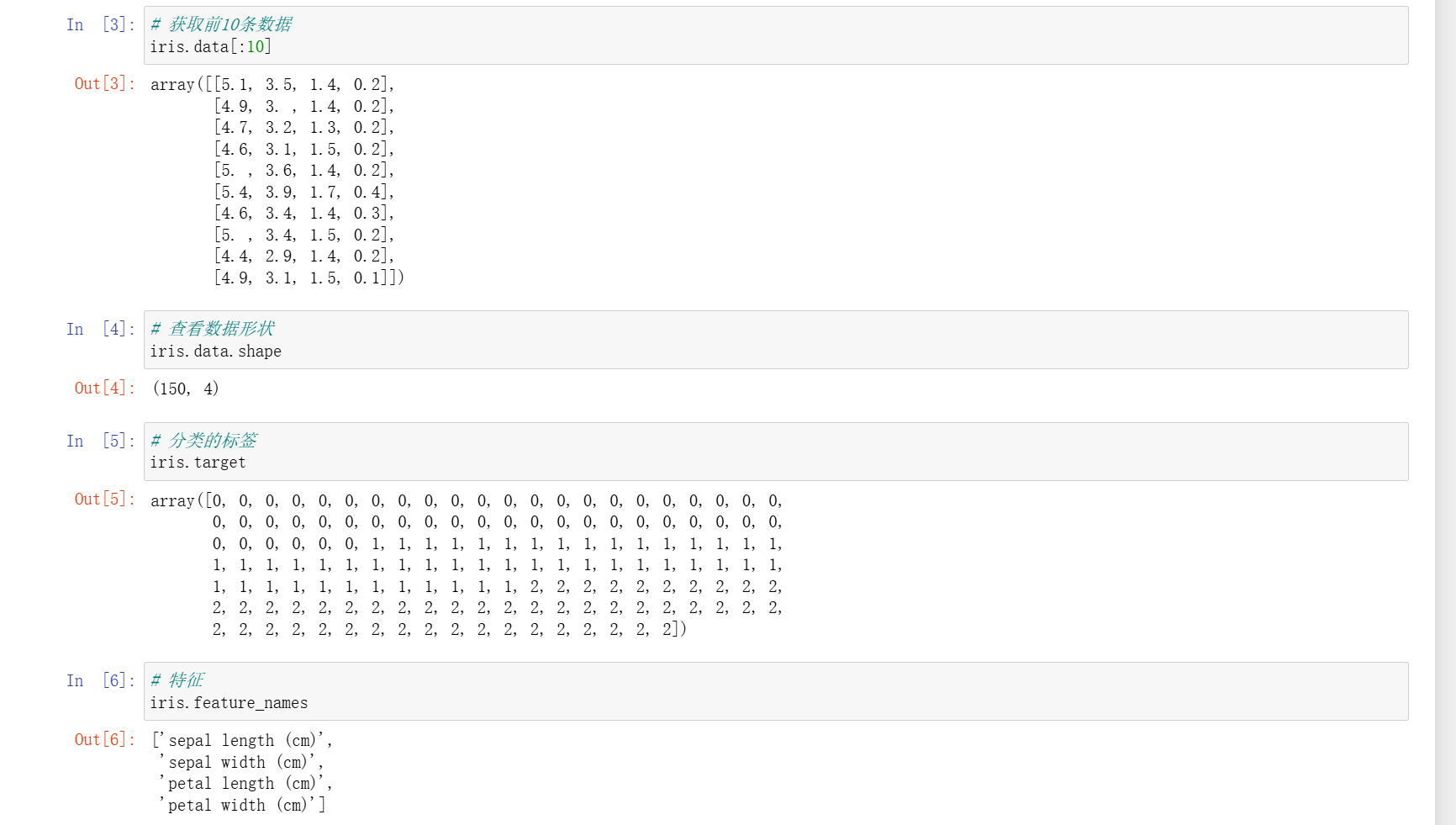
- 数据集介绍:鸢尾花数据集包含 3 个类别(Iris Versicolor、Iris Setosa、Iris Virginica),每个样本有 4 个特征(sepal length、sepal width、petal length、petal width)。
- 实现步骤:
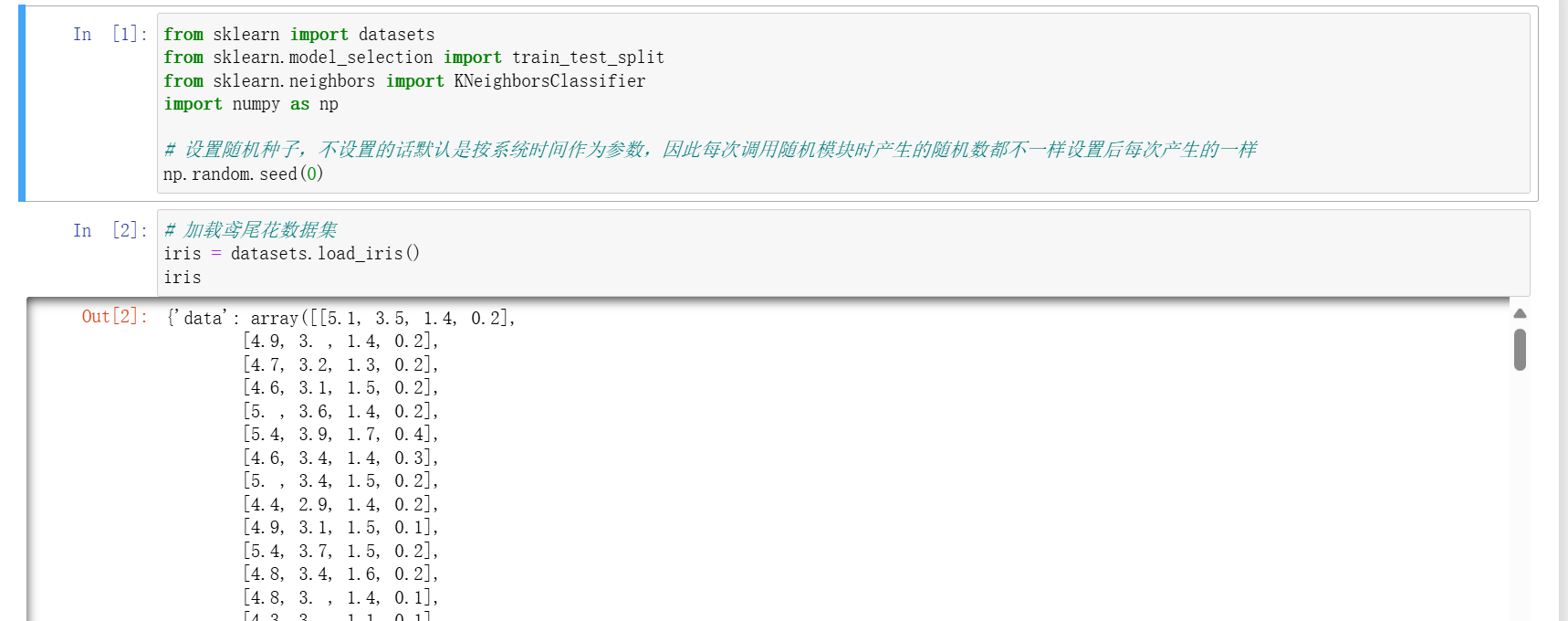
- 加载数据集:
iris = datasets.load_iris() - 查看数据信息:通过
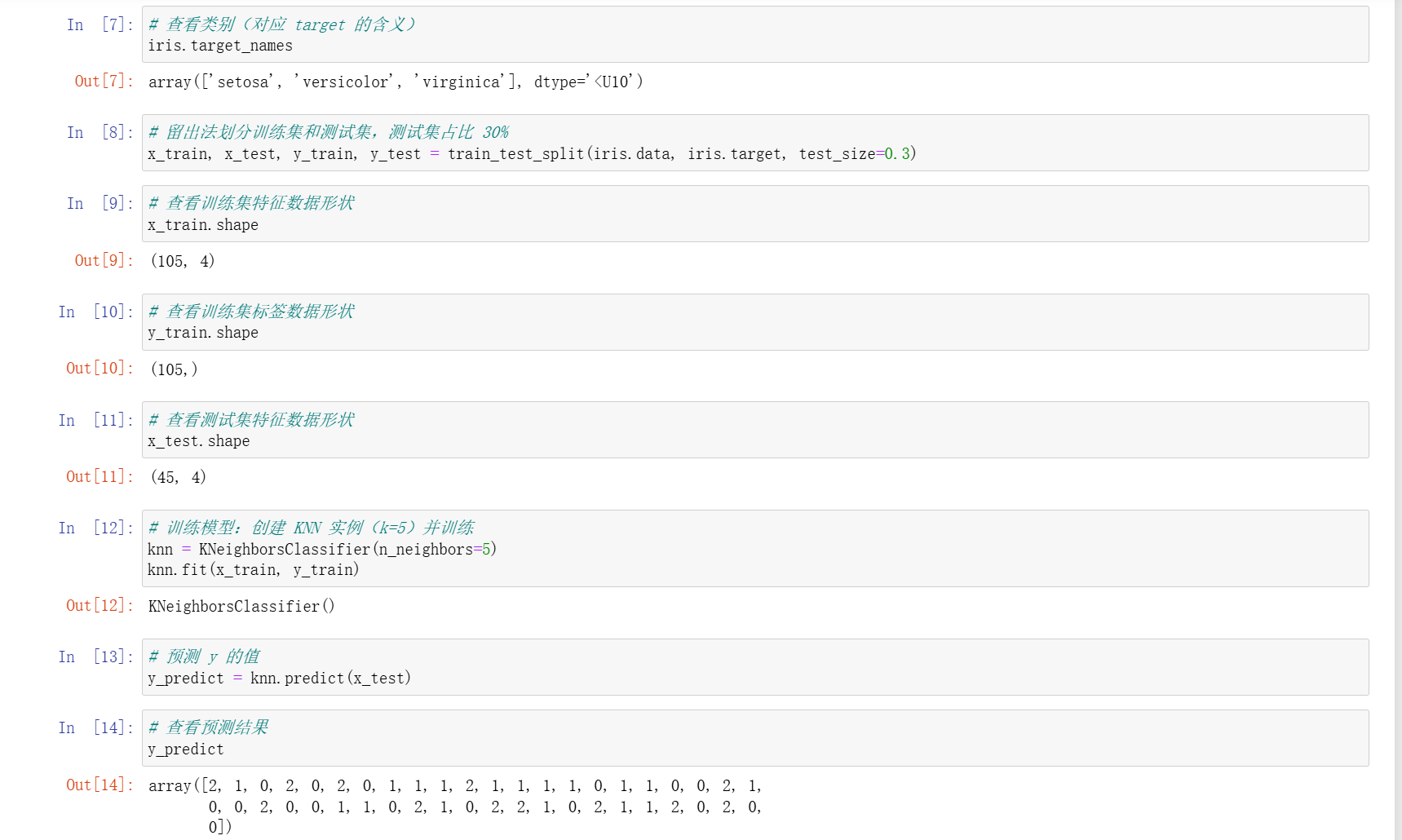
iris.target(分类标签)、iris.feature_names(特征名称)、iris.target_names(类别名称)了解数据 - 划分训练集和测试集:
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3) - 创建并训练模型:
knn = KNeighborsClassifier(n_neighbors=5, metric="euclidean"),knn.fit(x_train, y_train) - 模型评估:通过
knn.score(x_train, y_train)和knn.score(x_test, y_test)分别获取训练集和测试集得分 - 预测结果:
y_pred = knn.predict(x_test)
- 加载数据集:
我还自己尝试了一个水果测试的数据集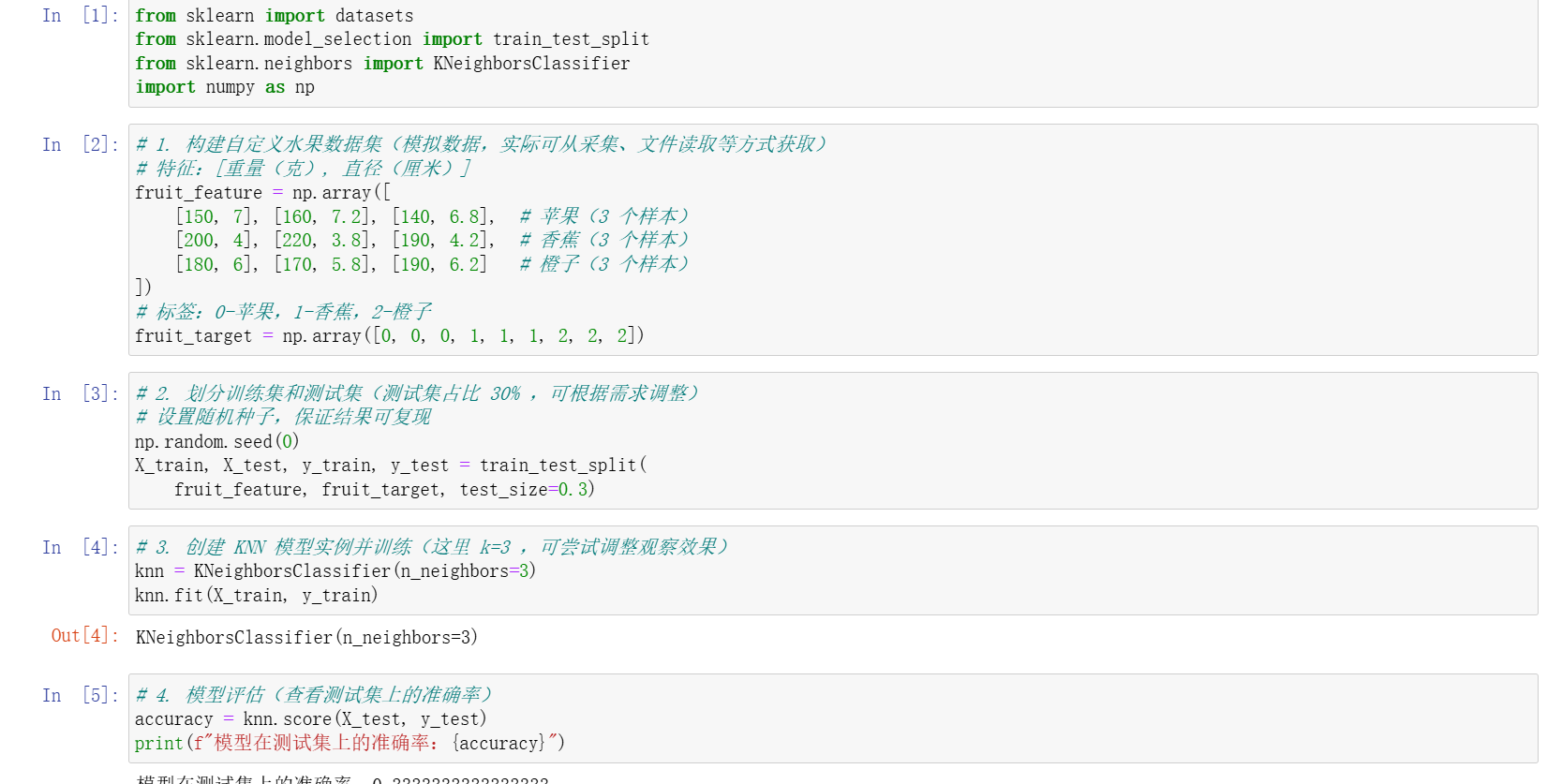
四、学习收获与总结
- 知识掌握:深入理解了 KNN 算法的原理和实现流程,掌握了欧式距离、曼哈顿距离等距离度量方法,学会了使用交叉验证选择最优 K 值,能够运用 sklearn 库实现基于 KNN 的分类任务。
- 实践能力:通过电影分类和鸢尾花分类案例,提升了将理论知识应用于实际问题的能力,熟悉了数据集加载、划分、模型训练、评估和预测的完整流程。
- 算法特点认知:认识到 KNN 算法是一种 “惰性学习” 算法,不需要预先训练模型,而是在预测时进行计算,其性能受 K 值和距离度量方式影响较大,在实际应用中需合理选择参数。
通过今天的学习,我不仅掌握了 KNN 算法的相关知识,也为后续学习其他机器学习算法奠定了基础,同时深刻体会到理论与实践结合的重要性。在今后的学习中,将进一步探索 KNN 算法的优化方法及在更多领域的应用。