Shader开发(十三)理解片元插值
在上一节中,我们成功创建了一个绚丽的彩虹三角形,见证了从三个不同颜色的顶点生成平滑渐变效果的神奇过程。但你是否好奇:GPU是如何仅凭3个顶点就生成成千上万个具有不同颜色的片元的? 今天,我们将探索片元插值的工作原理。
让我们先理解一个事实:
输入:仅有3个顶点,每个顶点包含位置和颜色信息
输出:可能数万个片元,每个都有独特的颜色值
过程:GPU通过数学插值算法实现这一转换
💡 思考一下:一个1024×768分辨率的三角形可能覆盖数十万个像素,但我们只定义了3个顶点的颜色。GPU是如何"猜出"中间所有像素的颜色的?
片元插值的原理
在示例项目中,三角形网格仅包含 3 个顶点。顶点着色器向 GPU 发送这些顶点的位置数据,GPU 则使用它们生成填充实心三角形的片元(像素数据)。由于片元位于顶点之间,GPU 需要决定如何分配顶点输出数据。
GPU 不会简单复制单一顶点的数据,而是从构成三角形面的 3 个顶点中混合数据。这种混合过程称为片元插值:
线性混合:插值在网格面上线性进行,仅基于当前面的顶点数据。
距离相关:片元颜色(或其它属性)根据其与顶点的相对距离计算,更靠近某个顶点的片元会继承更多该顶点的属性。
片元着色器中的所有 in 变量(如颜色)均通过这种方式从顶点数据插值得到。
片元插值(Fragment Interpolation)是计算机图形学中的核心技术,它解决了从稀疏的顶点数据生成密集的片元数据的问题。
基本原理:
顶点数据 → 光栅化 → 片元生成 → 插值计算 → 片元着色器
线性插值的数学基础
GPU使用重心坐标(Barycentric Coordinates)来实现片元插值:
// 对于三角形内任意一点P,其属性值为:
vec3 interpolatedColor = w1 * color1 + w2 * color2 + w3 * color3;
// 其中 w1 + w2 + w3 = 1.0(权重归一化)权重计算规律:
距离反比关系:离某个顶点越近,该顶点的权重越大
面积比例法:权重与子三角形面积成正比
线性保证:确保插值结果在顶点值的合理范围内
插值的约束条件
GPU插值遵循的规则:
只在单个三角形面内进行插值,绝不跨面
插值始终是线性的,保证平滑过渡
由GPU硬件直接计算,速度极快
使用浮点运算确保颜色精度
示例说明
假设三角形顶点分别为 R(红)、G(绿)和 B(蓝)。片元插值会生成中间颜色的片元:
中心片元:均衡混合 R、G、B。
靠近 R 的片元:包含更多红色。
此过程确保从有限顶点生成平滑渐变效果。
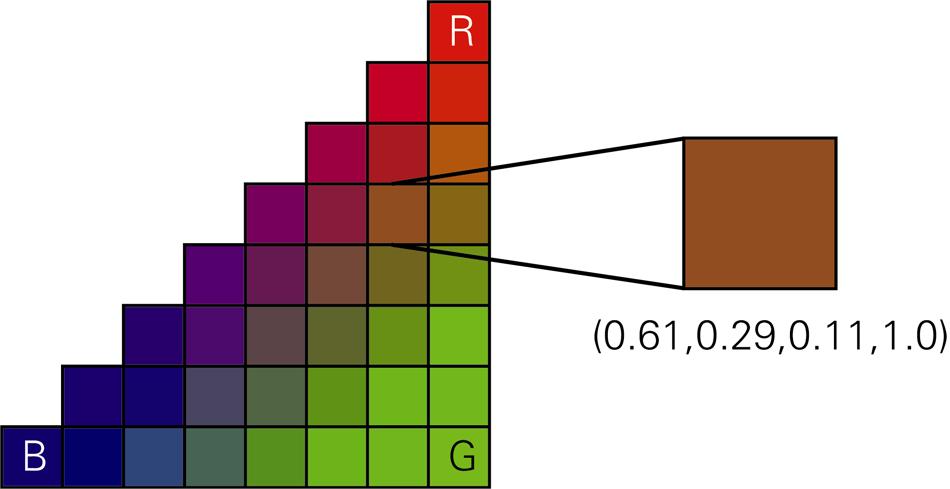
片元插值的实际效果
从上图中我们可以观察到:
红色区域(靠近R顶点)
权重分布:wR ≈ 0.7, wG ≈ 0.2, wB ≈ 0.1
颜色结果:主要是红色,略带绿色和蓝色成分
混合区域(三角形中心附近)
权重分布:wR ≈ 0.33, wG ≈ 0.33, wB ≈ 0.33
颜色结果:RGB均匀混合,呈现白色或灰色
绿色区域(靠近G顶点)
权重分布:wR ≈ 0.1, wG ≈ 0.7, wB ≈ 0.2
颜色结果:主要是绿色,带有少量其他色彩
图中高亮显示的片元展示了插值的精确性:
不在三角形几何中心,更靠近红色顶点
红色成分占主导,绿色和蓝色按距离比例减少
颜色值符合重心坐标的计算结果
片元插值的优势与局限
片元插值适用于逐顶点或逐片元变化的数据(如颜色渐变),高效利用 GPU 并行计算。但对于不变数据(如全局颜色),逐顶点存储会造成浪费。这类数据通常通过其他机制(如 uniform 变量)处理,后续章节将介绍。
uniform变量允许我们向着色器传递全局常量,避免不必要的顶点属性重复,大幅提升渲染效率。
