数据结构初阶(14)排序算法—交换排序(冒泡)(动图演示)
2.3 交换排序
2.3.0 基本思想
交换排序的基本思想:
基本思想
- 根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置。
(比较结果→交换位置)特点
- 将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
比 + 换
2.3.1 冒泡排序
基本逻辑
冒泡排序是一种非常直观的排序算法:遍历数组,每次比较两个元素,如果前者比后者大,则交换位置 ,重复的进行直至没有再需要交换,说明该数组排序完成。
每趟冒泡排序就是将当前最大的元素“沉底”。
冒泡排序的名字由来:越小的元素会经过交换慢慢"浮"到数组的顶端。
冒泡是一种形象的思想,但它主要是通过交换达到有序的。(交换排序)
动图演示
算法步骤
核心逻辑
- 外层循环控制轮数,共进行 n-1 轮遍历,n 为数组长度。
- 每轮内层循环比较相邻元素 arr[j] 和 arr[j+1],若前者较大则交换。
- 每轮结束后,当前未排序部分的最大值会“冒泡”到正确位置(数组末尾)。
优化方法
- 减少遍历范围:每轮外层循环后,数组末尾已有序,内层循环无需再比较已排序部分。
- 提前终止:引入exchange变量,如果在某轮内循环未发生交换,说明数组有序,可直接结束排序。
终止条件
- 外层循环完成n - 1次遍历,或exchange = false
代码实现
注意
- 函数的命名不建议使用拼音——MaoPaoPaiXu、MaoPaoSort、……
- 因为拼音需要配合音调使用,用拼音作函数名,做不到“见名知意”,代码的可读性极差
排序算法的实现,先实现单趟,再实现整体。
1. 先考虑单趟
- a[i]:第一趟若是a[1]~a[n-1]和前一个数据比较+交换。
- 初始化 i = 1;结束条件 i = n,循环 i < n
- a[i]:第一趟若是a[0]~a[n-2]和后一个数据比较+交换。
- 初始化 i = 0;结束条件 i = n - 1,循环 i < n - 1
2.再考虑整体
- 第一趟是a[1]~a[n-1],循环 i < n;每一趟就是 i < n - j
- 最后一趟就是只有a[1],循环 i < 2;j = n - 2;结束条件 j = n - 1,循环 j < n- 1
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 冒泡排序——一种交换排序
void BubbleSort(int* a, int n)
{//2.单趟变整体for (int j = 0; j < n - 1; j++) //注意控制0——n-1,一共需要排序n-1趟{//1.先考虑单趟,把最大的沉到最后int exchange = 0;for (int i = 1; i < n - j; i++) //注意控制1——n-j{//如果前一个更大if (a[i - 1] > a[i]) //i的起始是1,若i的起始是0,则a[i] > a[i+1],需要控制结束条件{//就交换一下Swap(&a[i - 1], &a[i]);exchange = 1;}}//如果某一趟冒泡排序没有发生交换if (exchange == 0)break;}
}代码测试。
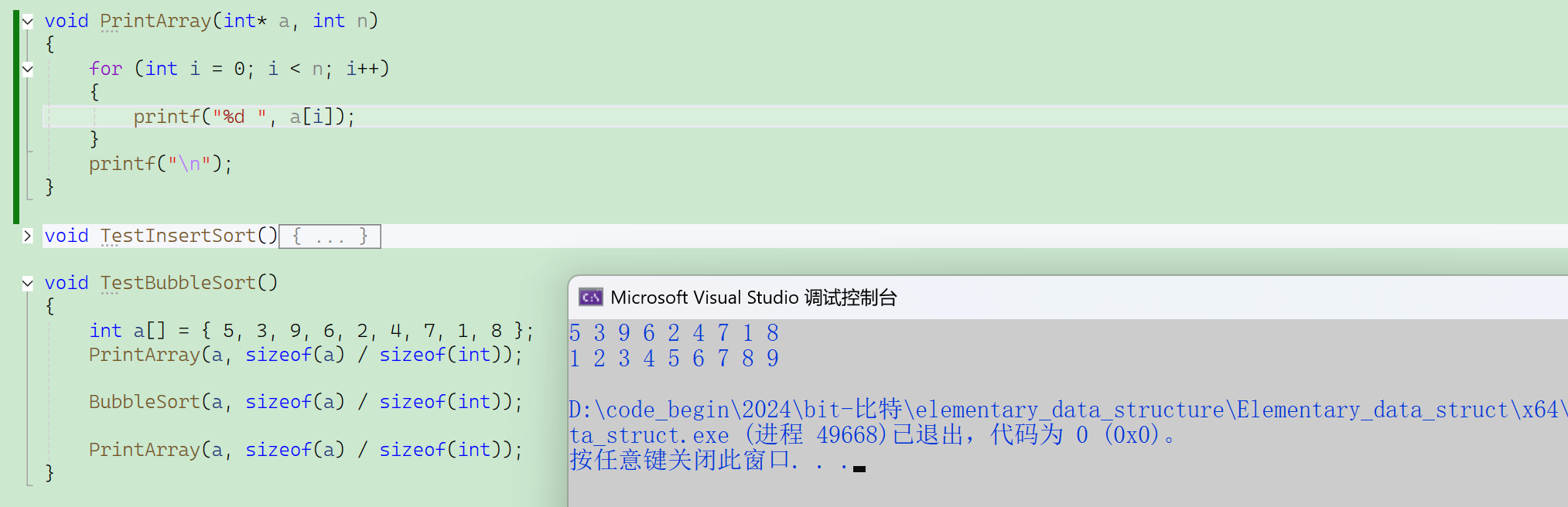
性能分析
最好情况:数组已经有序,此时只需要遍历一次,时间复杂度 O(n)。
最坏情况:数组完全倒序,此时需要比较n-1、n-2、……、1次,因此时间复杂度为O(n^2)。
时间复杂度:
情况 时间复杂度 说明 最优情况(已排序数组) O(N) 每趟只需比较一次,无需移动元素 最坏情况(完全逆序) O(N^2) 每次插入需比较和移动所有已排序元素 平均情况(随机数组) O(N^2) 平均需要 (N^2) / 4次比较和移动 空间复杂度:
- 空间复杂度:需常数额外空间O(1)——创建变量。
稳定性:
- 稳定
冒泡排序和插入排序的性能比较
注意
- 测性能的时候,需要使用release版本。
- 可能debug测出来性能差3倍,release测出来可能差10倍。
因为,debug要打各种调试信息进去,而且优化没有全开,编译器有些指令没有优化到极致,所以debug测出来就不能作为参考。- 而且实际的运行环境也是以release的方式运行的。
void TestOP()
{srand(time(0)); //要产生随机需要一个种子,否则随机是写死的伪随机const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N); //产生2个数组,每个数组含10万个元素int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i) //产生10万个元素,给2个数组{a1[i] = rand();a7[i] = a1[i];}int begin1 = clock(); //系统启动到执行到此的毫秒数InsertSort(a1, N);int end1 = clock(); //系统启动到执行到此的毫秒数//debug 版本,10万个数据,执行时差2425ms ——2.425s//release版本,10万个数据,执行时差605ms ——0.6s √//release版本,100万个数据,执行时差65971ms——65sint begin7 = clock();BubbleSort(a7, N);int end7 = clock();//debug 版本,10万个数据,执行时差 60526ms ——60s//release版本,10万个数据,执行时差11378ms——11.3s √//100万个数据,半天都跑不完 printf("InsertSort:%d\n", end1 - begin1);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a7);
}int main()
{//TestBubbleSort();TestOP();return 0;
}结论
- 虽然两个函数的时间复杂度相同(同一档),但是性能差距仍较大。
- 但是被认为是同一档。
- 时间复杂度只反映一个大概的量级。
不同量级的比较——冒泡排序和堆排序O(N*logN)
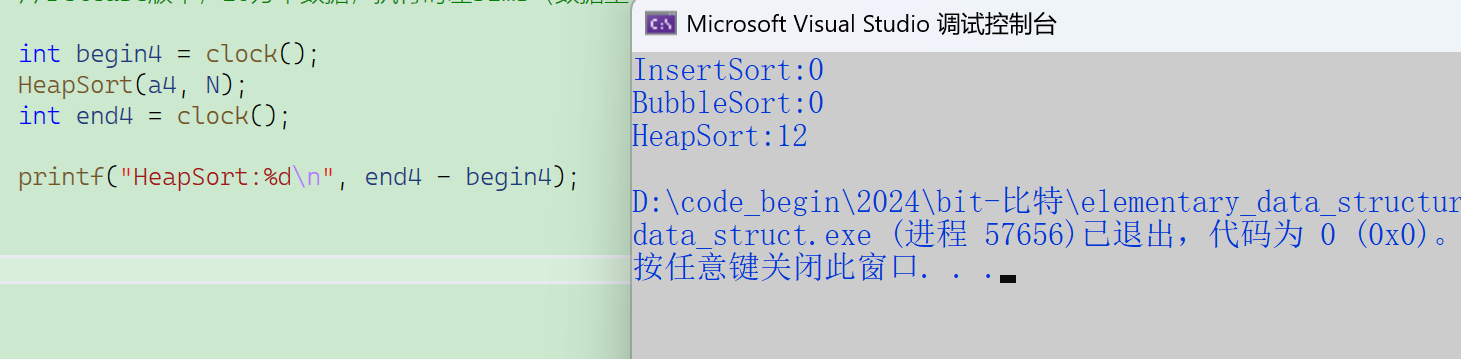
这还只是10万这个量级;
100万个数据:插入65971ms(65s),堆排序81ms,冒泡半天都跑不完。
结论
- 不同时间复杂度档次之间有很大的性能差异。
- 同一档内的不同算法,又有较大的性能差异。

插入比冒泡好很多的核心原因:就是因为插入的思想有非常强的适应性。
冒泡基本上提前终止很难(全有序),一般都要走到N^2——几乎每次都是最坏。
冒泡不再排序的条件是很苛刻的——全有序,在数据随机的情况下是很难达成的。
插入的思想,只有end+1的数据,比end前面的数据都小,才需要挪数据end次。
而挪动次数一般都达不到end次,因为一般都存在局部有序,只需要挪动部分数据——几乎每次都不是最坏。
特性总结
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序。(教学意义)
- 时间复杂度:O(N^2)。
- 空间复杂度:O(1)。
- 稳定性:稳定。
