DBSCAN 算法的原理

DBSCAN 是基于密度的聚类方法，它将簇定义为密度相连的点的最大集合，能够把密度足够高 + 连在一起的区域划分为簇，不受簇形状和噪声的影响。

一、DBSCAN 的核心概念：

• 两个算法参数：

  • Eps (Epsilon)：邻域半径，表示一个点的邻居范围
    • Eps 邻域：以某个点为圆心，以 Eps 为半径的圆（在更高维度中，圆变为超球面），称为这个点的 Eps 邻域
    • 密度 (Density)：Eps 邻域内点的个数
  • MinPts (Min Points)：构成一个簇的最小点数，表示一个点要成为核心点所需的最小邻居数，一个人为设定的阈限

• 三种点的类型：

  • 核心点 (Core Point)：如果某个点邻域半径内点的个数（含自身） >= MinPts，这个点就是核心点
  • 边界点 (Border Point)：如果某个点邻域半径内点的个数 < MinPts，且这个点本身在另一个核心点的邻域半径内（是一个核心点的邻居），这个点就是边界点
  • 噪声点 (Noise Point)：如果某个点既不是核心点，也不是边界点，它就是噪声点——也就是说这个点邻域半径内点的个数 < MinPts，且这个点本身不在任何核心点的邻域半径内（不是任何核心点的邻居）

• 四种点的关系：

  • 直接密度可达 (Directly Density Reachable)：如果 p 是一个核心点，q 在 p 的 Eps 邻域内（即q 和 p 之间的距离 <= eps），就称 q 是从 p 出发直接密度可达的
  • 密度可达 (Density Reachable)：如果存在一系列点 p1, p2, …, pn，其中每对相邻点 pi 和 pi+1 都是直接密度可达的，则点 p1 密度可达点 pn，即密度可达可以通过一系列的直接密度可达传递。
  • 密度连接 (Density Connected)：如果存在两个点 p 和 q，以及一个点 o，其中 o 到 p 密度可达，o 到 q 密度可达，就称 p 和 q 是密度相连的，q 和 p 也是密度相连的（即密度相连是对称的）。
    • o 到 p 密度可达：o 是核心点，p 在 o 的邻域内
    • o 到 q 密度可达：o 是核心点，q 在 o 的邻域内
    • p 和 q 之间不一定是密度可达的
  • 非密度相连：密度相连的两个点属于同一个聚类簇，非密度相连的两个点属于不同的聚类簇，或者其中存在噪声点。

点的类型示例

以下图为例：邻域半径 Eps = 1，MinPts = 4

• C1 - C7 为核心点，以其为圆心，Eps 为半径，圆内分别包含了 4、5、4、4、5、4 个点 >= 4，因此这些点是核心点
• B1 - B2 为边界点，以其为圆心，Eps 为半径，圆内分别包含了 2、2 个点 < 4，同时B1、B2 在核心点的邻域半径内，因此这些点是边界点
• N 为噪声点，以其为圆心，Eps 为半径，圆内包含了 1 个点 < 4，同时这个点在不在任何一个核心点的邻域半径内，因此这个点是噪声点

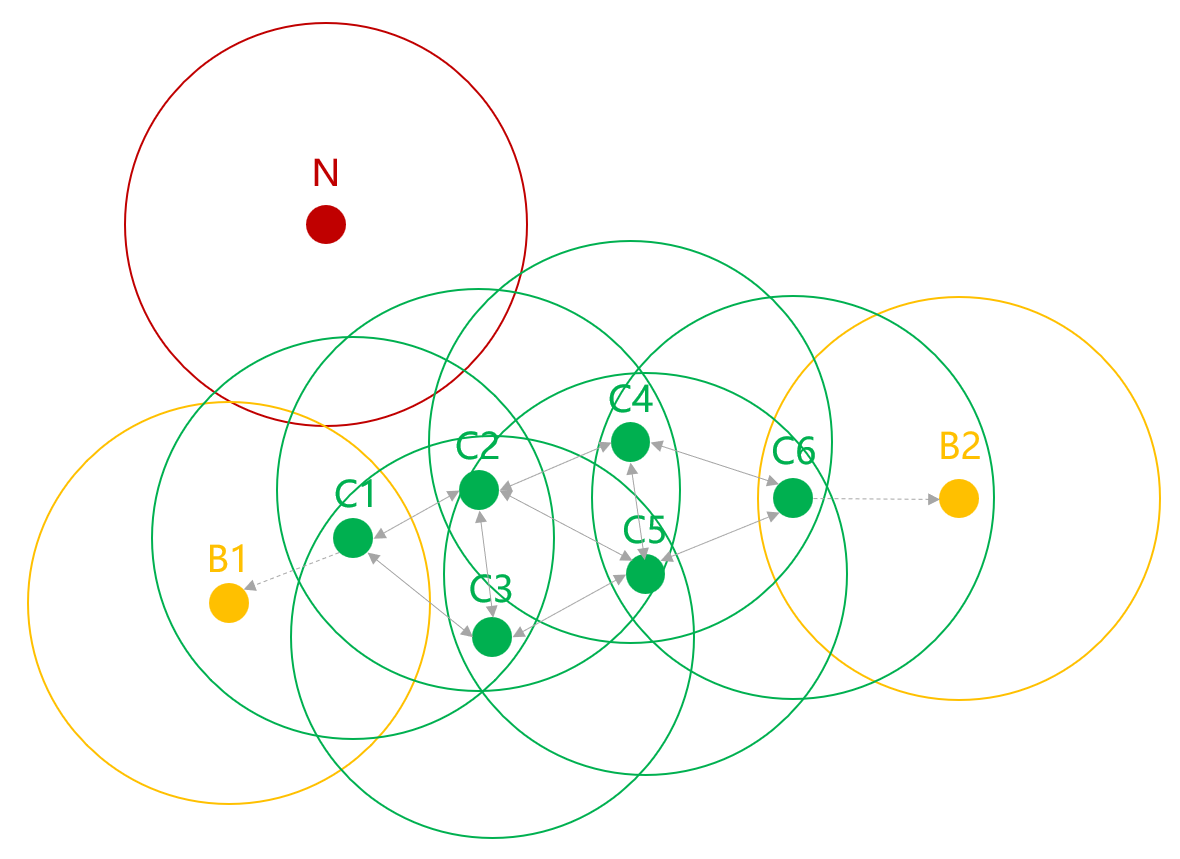
DBSCAN 算法的目标是找到密度相连对象的最大集合，并将密度相连的最大对象集合作为簇。

二、DBSCAN 聚类算法的步骤：

（1）寻找核心点，形成临时聚类簇

1）扫描全部样本点，找出全部核心点（邻域内点的数量 >= MinPts）

2）将这些点加入核心点列表，并且每个核心点和从它出发密度可达的点形成一个临时聚类簇（也就是核心点和它邻域内的所有点组成一个临时聚类簇）

（2）合并临时聚类簇，得到聚类簇

3）对于每个临时聚类簇，检查其中的点是否是核心点（是否在核心点列表中），如果是，将该核心点对应的临时聚类簇和当前聚类簇合并，得到新的临时聚类簇

4）重复此操作，直到当前临时聚类簇中的所有点，要么是核心点且从它出发密度直达的点都已经在该临时聚类簇内，要么是非核心点（也就是边界点）

5）将该临时聚类簇升级为聚类簇

（3）继续对剩余的临时聚类簇进行相同的合并操作，直到全部临时聚类簇都被处理

所有点，要么在聚类簇中，要么是噪声点

算法步骤示例

• 有数据集 D，n = 12，数据如下所示，取 eps = 1， MinPts = 4，使用 DBSCAN 算法对其进行聚类。

数据点	A	B	C	D	E	F	G	H	I	J	K	L
X1	2	5	1	2	3	4	5	6	1	2	5	2
X2	1	1	2	2	2	2	2	2	3	3	3	4

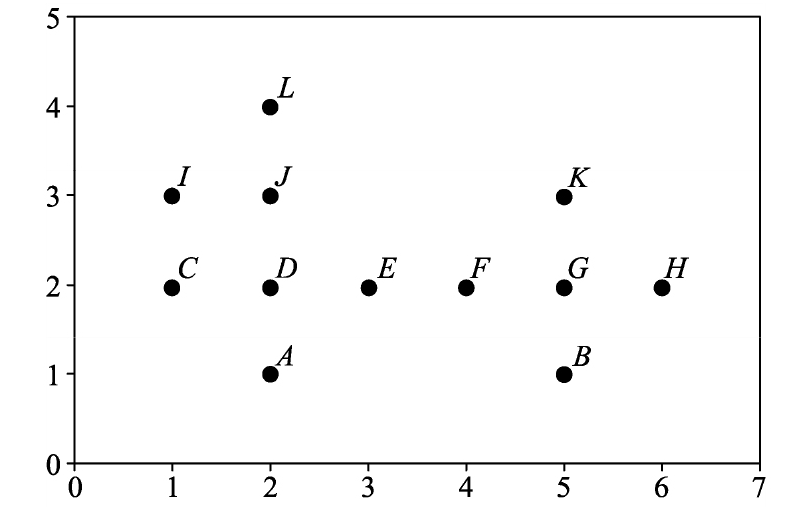
• 计算每个点到其他点的距离，使用欧式距离：

	A	B	C	D	E	F	G	H	I	J	K	L
A	0.0	3.0	1.4	1.0	1.4	2.2	3.2	4.1	2.2	2.0	3.6	3.0
B	3.0	0.0	4.1	3.2	2.2	1.4	1.0	1.4	4.5	3.6	2.0	4.2
C	1.4	4.1	0.0	1.0	2.0	3.0	4.0	5.0	1.0	1.4	4.1	2.2
D	1.0	3.2	1.0	0.0	1.0	2.0	3.0	4.0	1.4	1.0	3.2	2.0
E	1.4	2.2	2.0	1.0	0.0	1.0	2.0	3.0	2.2	1.4	2.2	2.2
F	2.2	1.4	3.0	2.0	1.0	0.0	1.0	2.0	3.2	2.2	1.4	2.8
G	3.2	1.0	4.0	3.0	2.0	1.0	0.0	1.0	4.1	3.2	1.0	3.6
H	4.1	1.4	5.0	4.0	3.0	2.0	1.0	0.0	5.1	4.1	1.4	4.5
I	2.2	4.5	1.0	1.4	2.2	3.2	4.1	5.1	0.0	1.0	4.0	1.4
J	2.0	3.6	1.4	1.0	1.4	2.2	3.2	4.1	1.0	0.0	3.0	1.0
K	3.6	2.0	4.1	3.2	2.2	1.4	1.0	1.4	4.0	3.0	0.0	3.2
L	3.0	4.2	2.2	2.0	2.2	2.8	3.6	4.5	1.4	1.0	3.2	0.0

• 在 eps 范围内，点数量 >= 4 的点有：D, G, J

• 聚类：

（1）扫描核心点，得到核心点列表 [D, G, J]

（2）每个核心点和从它出发密度可达的点形成一个临时聚类簇

• 从核心点 D 出发，可以得到临时聚类簇 [A, C, D, E, J]
• 从核心点 G 出发，可以得到临时聚类簇 [B, F, G, H, K]
• 从核心点 J 出发，可以得到临时聚类簇 [D, I, J, L]

（3）合并临时聚类簇

• 核心点 D 的临时聚类簇 [A, C, D, E, J] 中，包含另一个核心点 J
• 将 J 对应的临时聚类簇  [D, I, J, L] 和 D 对应的临时聚类簇合并，得到新的临时聚类簇 [A, C, D, E, I,  J, L]
• 新的临时聚类簇，只包含：①核心点，且从它出发密度直达的点都已经在该临时聚类簇内 ②非核心点
• 临时聚类簇升级为聚类簇 [A, C, D, E, I,  J, L]

（4）继续合并其他临时聚类簇

• 核心点 G 的临时聚类簇 [B, F, G, H, K] 中，不包含其他核心点
• 升级为聚类簇 [B, F, G, H, K]

（5）所有点均在聚类簇中，聚类完成

• 两个聚类簇：[A, C, D, E, I,  J, L]、[B, F, G, H, K]

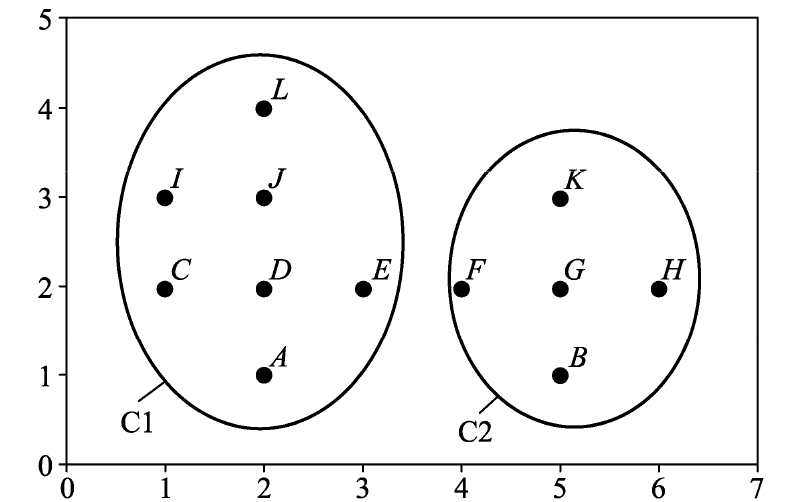
三、Eps 和 MinPts 值的确定

Eps 可以通过绘制 K-距离曲线（K-Distance Graph）来确定

K-距离：对于给定的 K ，对每个点，计算其对应的第 K 个最近邻点和它的距离，得到 K 距离值，并将所有点对应的 K 距离值按照降序排序，得到 K-距离曲线，曲线中第一个谷点位置对应的 K 距离值，是较好的 Eps 值选择。

K-距离曲线对 K 值的大小不敏感，一般可以将 K 值设置为4。

MinPts 的设置原则：（1）MinPts 不能为 1，因为 MinPts = 1 意味着每个点都是一个簇，没有意义；（2）MinPts 为2时，和层次距离最近邻域结果相同；（3）MinPts 应该选择 >= 3 的值；（4）MinPts 应该 >= dim + 1，dim 是待聚类数据的维度；MinPts 最好是维度数的 2 倍。

 

四、DBSCAN 算法的优缺点

优点：

不易受噪声影响——可以过滤低密度区域，发现稠密样本区域

能够发现任意形状的簇

不需要预先指定要聚类的簇数

缺点：

参数选取困难

不适合多密度数据和变化密度数据

数据集大时，收敛时间长

不适合高维数据