当前位置：首页 > news >正文

四分位数与箱线图

news 2025/8/15 23:03:52

四分位数

下限、Q1（25%值，又称第一四分位数）、中位数、Q3（75%值，又称第三四分位数）、上限、IQR（Inter Quartile Range，即四分位距）和异常值。

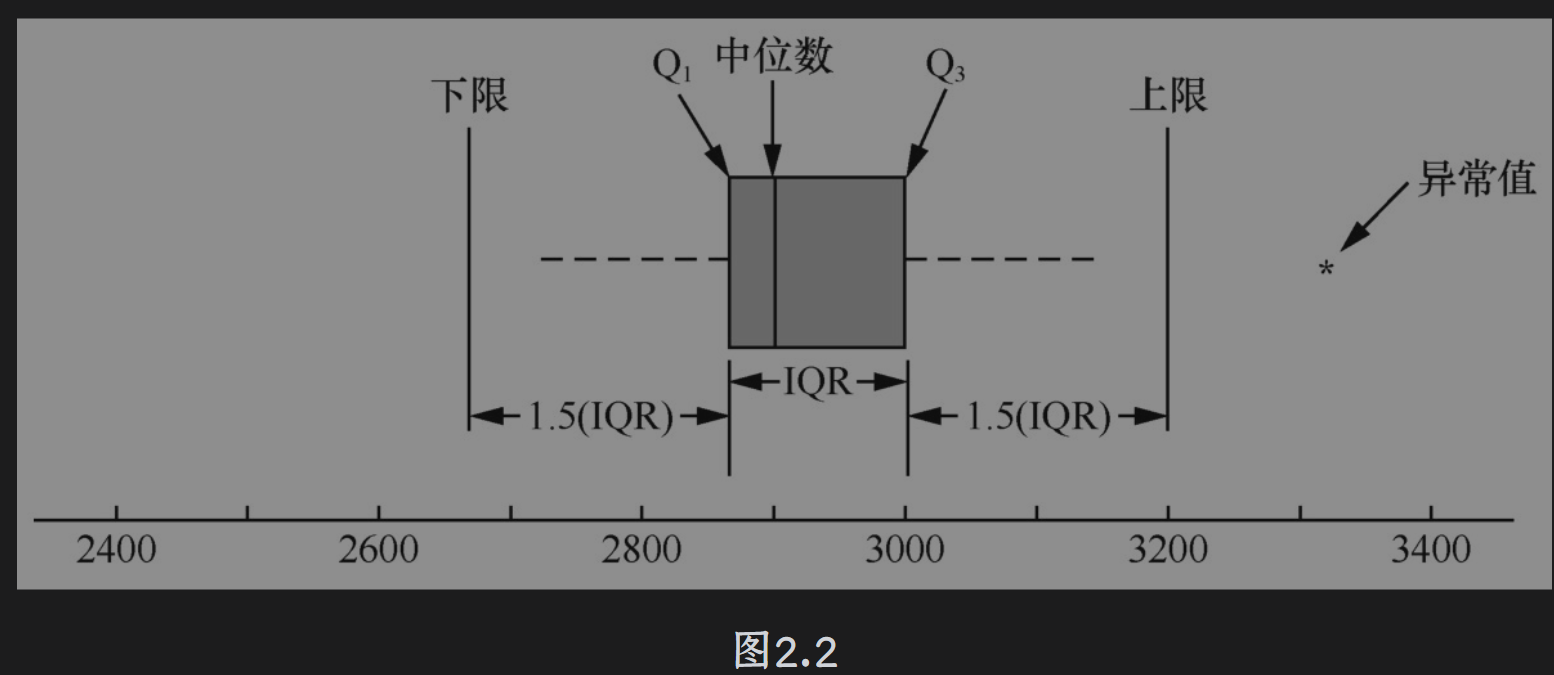
1. 四分位数的定义

四分位数是将一组有序数据分成四个等份的三个关键分割点，分别记为：
• Q1（第一四分位数）：第25%分位数，表示25%的数据小于或等于它。

• Q2（第二四分位数）：即中位数，第50%分位数。

• Q3（第三四分位数）：第75%分位数，表示75%的数据小于或等于它。

通过这三个点，可以快速了解数据的分布范围和集中趋势。

2. 四分位数的计算方法

步骤1：将数据从小到大排序

数据必须是有序的才能计算四分位数。

步骤2：确定中位数（Q2）

• 如果数据量（n）为奇数，中位数是正中间的数。

• 如果n为偶数，中位数是中间两个数的平均值。

步骤3：计算Q1和Q3

• Q1：数据下半部分的中位数（即小于Q2的部分）。

• Q3：数据上半部分的中位数（即大于Q2的部分）。

📌 注意：不同统计软件（如Excel、R、Python）对四分位数的计算规则可能略有差异（例如是否包含中位数），但核心逻辑一致。

3. 实例演示

例子1：奇数个数据

数据：[3, 7, 8, 5, 12, 14, 21, 13, 18]
步骤1：排序 → [3, 5, 7, 8, 12, 13, 14, 18, 21]
步骤2：找Q2（中位数）
• 共9个数，中位数是第5个数 → Q2 = 12

步骤3：找Q1和Q3
• Q1：下半部分 [3, 5, 7, 8] 的中位数 → (5+7)/2 = 6

• Q3：上半部分 [13, 14, 18, 21] 的中位数 → (14+18)/2 = 16

结果：Q1=6, Q2=12, Q3=16

例子2：偶数个数据

数据：[1, 3, 5, 7, 9, 11, 13, 15]
步骤1：已排序
步骤2：找Q2
• 共8个数，中位数是第4、5个数的平均值 → (7+9)/2 = 8

步骤3：找Q1和Q3
• Q1：下半部分 [1, 3, 5, 7] 的中位数 → (3+5)/2 = 4

• Q3：上半部分 [9, 11, 13, 15] 的中位数 → (11+13)/2 = 12

结果：Q1=4, Q2=8, Q3=12

4. 四分位数的应用

（1）箱线图（Boxplot）
• 箱体范围：Q1到Q3（IQR = Q3 - Q1）。

• 箱内线：Q2（中位数）。

• 异常值：通常定义为小于 Q1 - 1.5×IQR 或大于 Q3 + 1.5×IQR。

（2）数据分布分析
• 对称分布：Q2 - Q1 ≈ Q3 - Q2。

• 右偏分布：Q3 - Q2 > Q2 - Q1（数据向右延伸）。

• 左偏分布：Q2 - Q1 > Q3 - Q2（数据向左延伸）。

（3）识别异常值
例如，若Q1=6, Q3=16，则：
• IQR = 16 - 6 = 10

• 异常值边界：6 - 1.5×10 = -9 和 16 + 1.5×10 = 31

• 任何小于-9或大于31的数据点均为异常值。

5. 常见问题

Q1：四分位数和百分位数有什么关系？
• Q1 = 25%分位数，Q2 = 50%分位数，Q3 = 75%分位数。

Q2：如果数据有重复值怎么办？
计算方法不变，重复值需保留排序后的位置。
例如：[2, 4, 4, 6, 8]的Q1是第25%位置的值 → 取第2个数 4。

Q3：Excel中如何计算四分位数？
• 使用函数 QUARTILE.INC(data, quart)，其中 quart=1,2,3 分别对应Q1/Q2/Q3。

总结

四分位数是描述数据分布的核心工具，尤其适用于：
• 快速了解数据的离散程度（通过IQR）。

• 检测异常值。

• 比较不同数据集的分布（如箱线图对比）。

箱线图

参考：Python学习笔记：异常值检测之箱线图 - Hider1214 - 博客园

1. 箱线图的定义

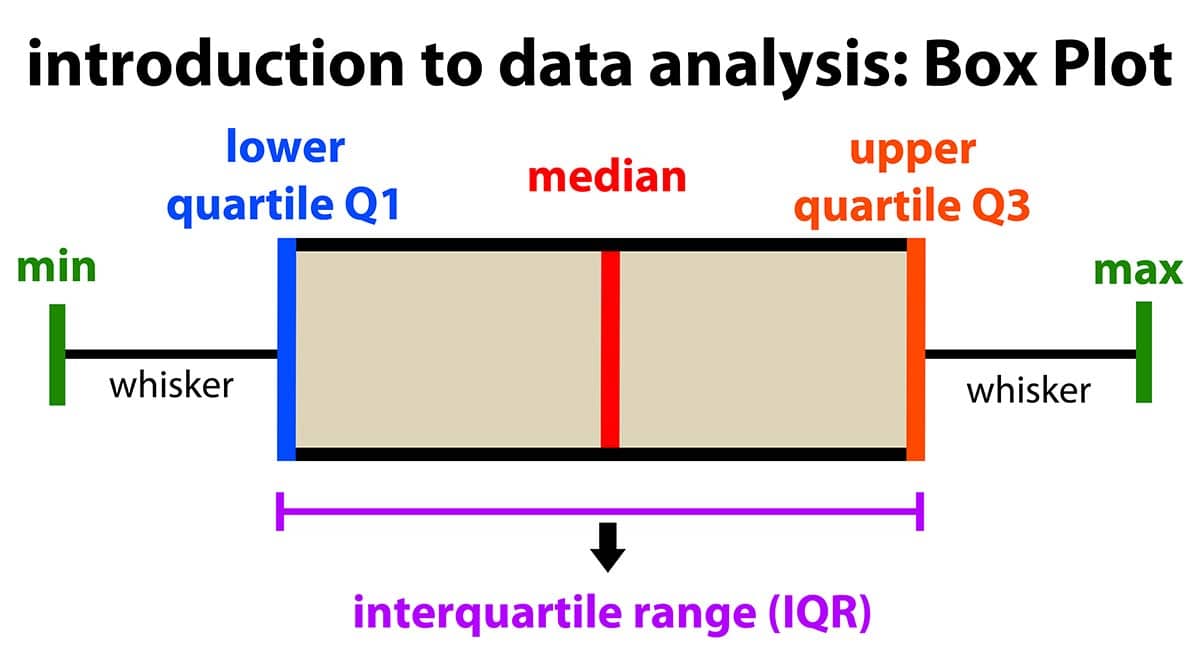
箱线图是一种可视化数据分布的图表，通过五个关键统计量（最小值、Q1、Q2、Q3、最大值）和异常值检测，直观展示数据的：
• 集中趋势（中位数）

• 离散程度（四分位距IQR）

• 偏态与异常值

2. 箱线图的构造

核心组成部分

箱体（Box）：
1. 下边缘：第一四分位数（Q1）。
2. 箱内线：中位数（Q2）。
3. 上边缘：第三四分位数（Q3）。
4. 箱体高度 = IQR（Q3 - Q1），反映中间50%数据的分布范围。
须线（Whiskers）：
1. 上须：延伸到不超过 Q3 + 1.5×IQR 的最大值。
2. 下须：延伸到不低于 Q1 - 1.5×IQR 的最小值。
异常值（Outliers）：超出须线范围的数据点，通常用圆点或星号标记。

📌 示意图

     最大值（非异常值）|
Q3 +-------+   Q3 + 1.5×IQR（上限）|-----|      ○ 异常值Q2  |  ┃  | |-----|
Q1 +-------+   Q1 - 1.5×IQR（下限）|最小值（非异常值）

3. 箱线图的绘制步骤（以实际数据为例）

数据集：[12, 15, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 30, 40]

步骤1：计算四分位数
• Q1 = 第25%位数 → 18

• Q2 = 中位数 → 21.5

• Q3 = 第75%位数 → 24

• IQR = Q3 - Q1 = 6

步骤2：确定须线边界
• 上须边界 = Q3 + 1.5×IQR = 24 + 9 = 33

• 数据中 ≤33的最大值是 30，因此上须延伸到30。

• 下须边界 = Q1 - 1.5×IQR = 18 - 9 = 9

• 数据中 ≥9的最小值是 12，因此下须延伸到12。

步骤3：标记异常值
• 40 > 33 → 40是异常值，单独标记。

最终箱线图

       ○ 40|
30 ----+       |-------|
24   | 21.5  ||-------|
18 ----+|
12 ----+

4. 箱线图的解读技巧

（1）分布形态判断
• 对称分布：中位数（Q2）在箱体中央，须线长度相近。
• 右偏分布：Q2靠近Q1，上须较长（如收入数据）。

• 左偏分布：Q2靠近Q3，下须较长。

（2）异常值检测
• 任何超出 [Q1-1.5×IQR, Q3+1.5×IQR] 的数据点均为潜在异常值。

（3）比较多组数据
并列箱线图可直观对比不同组别的分布差异（如下图）。

5. 箱线图的优缺点

优点：
• 直观展示数据分布和异常值。

• 适用于小样本和大样本数据。

• 节省空间，适合多组数据对比。

缺点：
• 隐藏了数据的具体分布形状（如双峰分布需结合直方图）。

• 对极端异常值敏感（可调整1.5×IQR的倍数）。

6. 实际应用场景

学术研究：比较实验组与对照组的成绩分布。
商业分析：分析不同地区销售额的离散程度。
质量控制：检测生产线的产品尺寸是否稳定。

案例：学生考试成绩对比

班级	箱线图关键值
A班	Q1=60, Q2=75, Q3=85, 异常值：95
B班	Q1=70, Q2=80, Q3=90, 无异常值

解读：A班成绩分散且存在高分异常，B班成绩更集中。

7. 常见问题解答

Q1：箱线图和直方图如何选择？
• 箱线图：快速比较多组数据的分布和异常值。

• 直方图：展示单组数据的详细分布形状（如是否双峰）。

Q2：为什么用1.5×IQR定义异常值？
• 基于经验法则（Tukey's Fence），覆盖约99.3%的正态分布数据。

Q3：如何用Python绘制箱线图？

import matplotlib.pyplot as plt
data = [[12,15,17,18,19,20,21,22,23,24,25,26,30,40]]
plt.boxplot(data)
plt.show()

8. 如何科学解读箱线图

1. 箱线图的五大核心要素
首先明确箱线图的每个部分代表的含义：

箱体（Box）：覆盖中间50%的数据（Q1到Q3）。
中位数线（Q2）：箱体内的横线，反映数据集中趋势。
须线（Whiskers）：延伸至正常范围的最大最小值。
异常值（Outliers）：超出须线的离散点。
IQR（四分位距）：Q3 - Q1，衡量数据离散程度。

2. 分步骤解读指南
步骤1：看中位数（Q2）的位置
• 中位数靠近箱体底部（Q1） → 数据可能右偏（尾部向右延伸）。

• 中位数靠近箱体顶部（Q3） → 数据可能左偏（尾部向左延伸）。

• 中位数在箱体中央 → 数据分布较对称。

示例：若中位数线在箱体下半部，说明更多数据集中在较小值区域（如收入数据常见右偏）。

步骤2：观察箱体高度（IQR）
• 箱体越宽 → 数据离散程度越大（中间50%数据分布分散）。

• 箱体越窄 → 数据越集中。

示例：比较A/B两组箱线图，A组IQR=20，B组IQR=5 → B组数据更稳定。

步骤3：分析须线长度
• 上须长于下须 → 数据右侧有更多极端大值（右偏）。

• 下须长于上须 → 数据左侧有更多极端小值（左偏）。

• 须线对称 → 数据分布可能对称。

示例：若上须延伸到很远，而下须很短，说明存在少数极大值（如富豪收入拉长右尾）。

步骤4：识别异常值
• 异常值单独标记（如圆圈或星号）。

• 需结合业务判断是否剔除或处理（如传感器故障数据）。

示例：某班级考试成绩箱线图中，有一个异常低分（40分），需调查是否缺考或作弊。

3. 实际案例解析：电商销售额箱线图

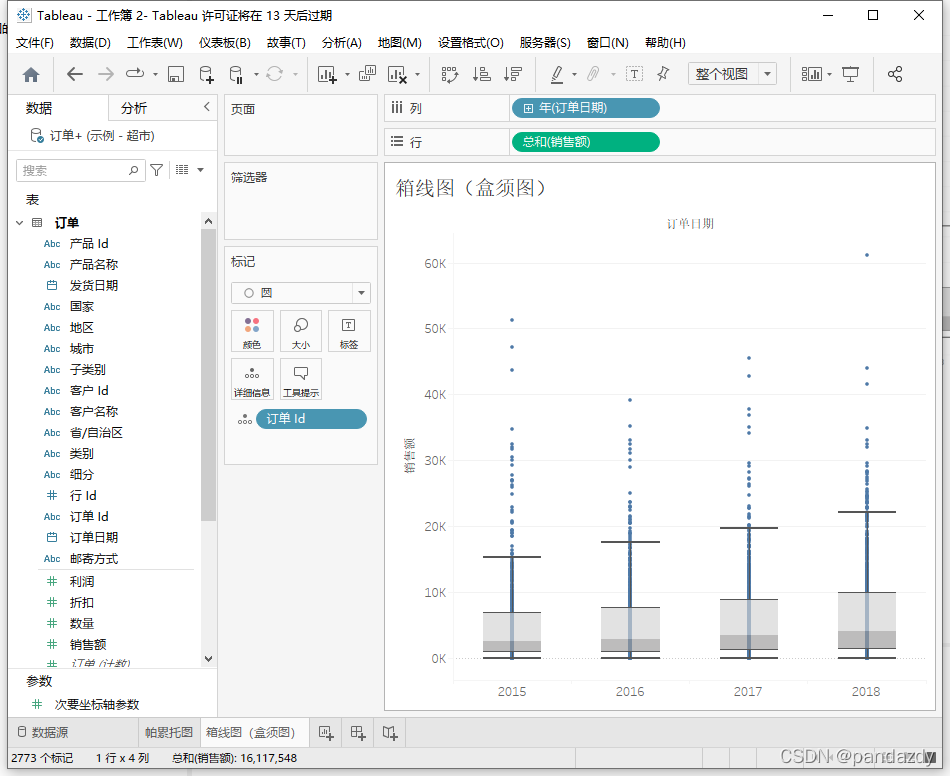
• Q2（中位数）：靠近箱体底部 → 多数订单金额较低，少数高额订单拉高均值（右偏）。

• IQR：箱体较窄 → 大部分订单金额集中在小范围内。

• 异常值：多个极高值 → 可能存在大客户或刷单行为。

4. 常见分布形态判断

箱线图形状	数据分布特征
中位数居中，须线对称	近似对称分布（如正态分布）
中位数靠近Q1，上须长	右偏分布（如收入数据）
中位数靠近Q3，下须长	左偏分布（如考试成绩满分堆积）
箱体窄，须线短	数据高度集中
箱体宽，异常值多	数据分散且存在极端值

5. 解读时的注意事项

结合业务背景：异常值可能是错误数据，也可能是关键信息（如医疗中的罕见病例）。
样本量影响：小样本时箱线图可能不稳定，需谨慎解读。
补充其他图表：若发现双峰分布（如箱体分裂），需用直方图验证。

6. 实战练习
数据集：[22, 23, 24, 24, 25, 26, 27, 28, 29, 30, 50]

你的任务：

计算Q1、Q2、Q3和IQR。
判断是否存在异常值。
描述数据分布形态。

答案：

Q1=24, Q2=26, Q3=29, IQR=5
异常值边界：24-7.5=16.5，29+7.5=36.5 → 50是异常值。
中位数略低于箱体中心，上须极长 → 明显右偏，存在极端大值。

总结
箱线图的本质是用五个数字概括数据分布，快速判断数据偏态和离散程度，识别异常值，比较多组数据差异。

补充知识一：数据的测量尺度

数据的测量尺度（Measurement Scale） 是指数据的分类方式，反映了数据的性质、可进行的数学运算以及适用的统计分析方法，它决定了你能用这些数据做什么样的计算和分析。

通常分为 4 种测量尺度，从低到高依次为：

在统计学中，数据的测量尺度（Measurement Scale） 是指数据的分类方式，反映了数据的性质、可进行的数学运算以及适用的统计分析方法。它决定了你能用这些数据做什么样的计算和分析。

通常分为 4 种测量尺度，从低到高依次为：

1. 名义尺度（Nominal Scale）

特点：数据仅用于分类或标记，没有顺序、大小或数学意义。
例子：
- 性别（男、女、其他）
- 颜色（红、蓝、绿）
- 国家（中国、美国、日本）
可进行的运算：
- 计算频数（如“男性有多少人”）
- 计算众数（哪个类别出现最多）
- 不能计算平均数、中位数（因为类别没有数值意义）
统计方法：卡方检验、列联表分析

2. 顺序尺度（Ordinal Scale）

特点：数据可以排序，但无法精确衡量差异大小。
例子：
- 教育程度（小学、中学、大学、研究生）
- 满意度评分（非常不满意、不满意、一般、满意、非常满意）
- 比赛名次（第一名、第二名、第三名）
可进行的运算：
- 可以计算中位数、百分位数
- 可以比较大小（如“大学学历 > 中学学历”）
- 但不能计算平均数（因为“非常满意”比“满意”高多少无法量化）
统计方法：秩和检验（如 Mann-Whitney U 检验）、Spearman 等级相关

3. 等距尺度（Interval Scale）

特点：数据有顺序，且可以计算差异，但没有绝对零点（即“0”不代表完全没有）。
例子：
- 温度（摄氏度或华氏度，0°C 不代表没有温度）
- IQ 分数（0 分不代表完全没有智力）
- 年份（2020 年、2021 年，但“0 年”是人为设定的）
可进行的运算：
- 可以计算平均数、标准差
- 可以加减（如“30°C 比 20°C 高 10°C”）
- 但不能乘除（因为“20°C 不是 10°C 的两倍热”）
统计方法：t 检验、ANOVA、Pearson 相关

4. 比率尺度（Ratio Scale）

特点：数据有顺序、可计算差异，且有绝对零点（“0”代表完全没有）。
例子：
- 身高（0 cm 代表没有高度）
- 体重（0 kg 代表没有重量）
- 收入（0 元代表没有收入）
- 反应时间（0 秒代表没有时间）
可进行的运算：
- 可以计算所有统计量（平均数、中位数、标准差等）
- 可以加减乘除（如“100 kg 是 50 kg 的两倍”）
统计方法：所有参数检验（回归分析、t 检验等）

总结表格

测量尺度	特点	例子	可计算统计量	适用统计方法
名义尺度	分类，无顺序	性别、颜色	频数、众数	卡方检验
顺序尺度	可排序，但差异无意义	满意度、名次	中位数、百分位数	秩和检验
等距尺度	可计算差异，无绝对零点	温度、IQ	平均数、标准差	t 检验、ANOVA
比率尺度	可计算比例，有绝对零点	身高、收入	所有统计量	回归分析