二叉搜索树的C语言实现

简介

        二叉搜索树也叫二叉排序树、二叉查找树，不一定是完全二叉树，满足以下性质：

        1、非空左子树的所有键值小于其根结点的键值

        2、非空右子树的所有键值大于其根结点的键值

        3、左右子树均是二叉搜索树

        4、对二叉排序树进行中序遍历可以得到一个递增的有序序列。

        由于是二叉树，所以树的每个结点都有两个指针域分别指向左孩子、右孩子和一个数据域。

typedef int ElemType;typedef struct Tree_Node
{struct Tree_Node *left;ElemType data;struct Tree_Node *right;
}*BinTree;

        对二叉搜索树的操作包括查找特定数据、查找最小数据、查找最大数据、插入元素、删除特定元素。

查找

查找特定数据

        查找是从根结点开始，如果树为空，返回NULL。

        若搜索树非空，则根结点关键字和要查找的数据x对比，并进行不同处理：

        1、x小于根结点键值，只需在左子树搜索。

        2、x大于根结点键值，只需在右子树搜索。

        3、x等于根结点键值，搜索完成。

BinTree BinTree_find(BinTree tree,ElemType data)
{BinTree current = tree;while (current){if(data > current->data)current = current->right;else if(data < current->data)current = current->left;else if(data == current->data)break;}return current;
}

查找最值数据

        由二叉搜索树的性质：左孩子结点的数据一定小于父结点的数据，右孩子结点的数据一定大于父结点的数据，所以最大数据一定在二叉搜索树的最右分支的端结点上，最小数据一定在二叉搜索树的最左分支的端结点上。

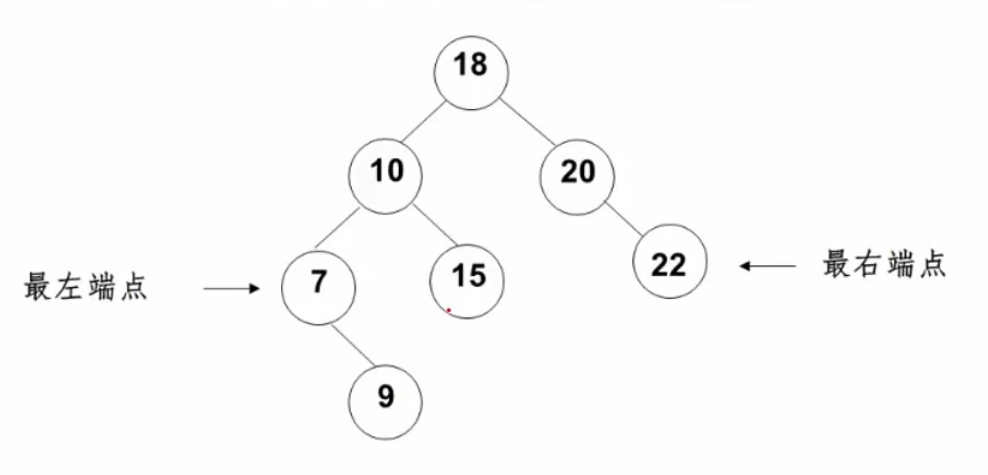
BinTree BinTree_find_max(BinTree Tree)
{if(Tree == NULL)return;BinTree current = Tree;while (current->right){current = current->right;}return current;
}BinTree BinTree_find_min(BinTree Tree)
{if(Tree == NULL)return;BinTree current = Tree;while (current->left){current = current->left;}return current;
}

插入

        进行二叉搜索树的插入操作时，关键是要找到元素应该插入的位置，可以采用类似find的方法。

        基本思想就是将要插入的元素X和根结点的键值相比较，根据大小来决定往右或者往左找，直至找到一个结点为空，插入元素并挂在父结点上。

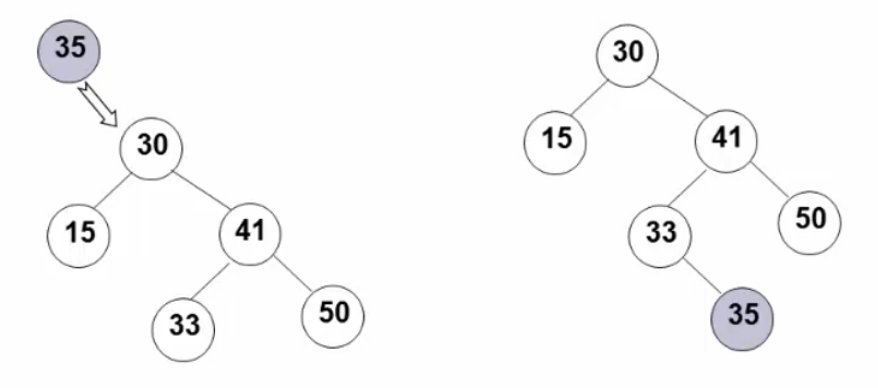
BinTree BinTree_insert(BinTree tree,ElemType data)
{//当前结点为空，插入新元素if(tree == NULL){tree = (BinTree)malloc(sizeof(struct Tree_Node));tree->data = data;tree->left = tree->right = NULL;}//若插入数据大于当前结点，递归插入右子树if(data > tree->data)tree->right = BinTree_insert(tree->right,data);else if(data < tree->data)//若插入数据小于当前结点，递归插入左子树tree->left = BinTree_insert(tree->left,data);//若插入数据等于当前结点，返回原树//当有新元素插入时，也会是相等的情况，也避免了重复插入return tree;
}

删除

        删除操作和查找的关系比较密切，查找到该元素所在的位置（其实应该查找到该元素的父结点的位置和相对于父结点的方向，左/右），但是删除操作的实现比较复杂，需要讨论多种情况：待删除结点记作该结点。

        1、该结点没有左子树：根据二叉搜索树的结构要求，要使该结点的父结点的左/右指针指向该结点的右子树，之后释放该结点。这种情况也包括了右子树为空的情况（叶子结点）。若右子树为空（即该结点为叶子结点），则指向NULL，正确。

        2、该结点没有右子树：前面已经讨论了该结点没有左子树的情况，如果使用if-else结构的话，那么本情况下该结点一定有左子树。根据二叉搜索树的结构要求，要使该结点的父结点的左/右指针指向该结点的左子树，之后释放该结点。

        3、该结点既有左子树又有右子树：此时为了二叉搜索树的结构要求，应该从左子树的最右侧结点或者右子树的最左侧结点来替换该结点。因为从左子树拿出最大值，才能使左子树的结点都小于该结点，因为是左子树的结点，所以肯定小于右子树的结点；或者从右子树拿出最小值，才能使右子树的结点都大于该结点，因为是右子树的结点，所以肯定大于左子树的结点。我更倾向于选择左子树的最右侧结点。选择左子树的最右侧结点时又分两种情况：

        （1）该结点的左孩子结点就是左子树的最右侧结点：此时应该让左孩子结点的值覆盖该结点的值，使该结点的左指针更新，替换为左孩子结点的左指针（左孩子结点没有右子树，因为他已经是最右侧结点了），即使左孩子结点的左指针为NULL也正确。之后释放最右侧结点。

        （2）该结点的左子树的最右侧结点另有其人：此时应该让最右侧结点的值覆盖该结点的值，使最右侧结点的父结点的右指针更新，替换为最右侧结点的左指针（最右侧结点没有右孩子了），之后释放最右侧结点。

BinTree BinTree_delete(BinTree tree,ElemType data)
{BinTree current = tree;//当前结点int flag = 0;//0代表当前结点是父结点的左孩子，1代表是右孩子BinTree pre = NULL;//当前结点的父结点//找到要删除的结点while (current){if(data > current->data){//更新父结点pre = current;//更新当前结点current = current->right;//更新左/右flag = 1;}else if(data < current->data){pre = current;current = current->left;flag = 0;}else if(data == current->data)break;}//该元素不存在if(current == NULL)return tree;//该元素没有左孩子结点,根据当前结点相对于父结点的关系，更新父结点指向其右子树if(current->left == NULL){//若父结点为空则代表删除的结点是根结点，只需要释放当前结点,并返回右子树//否则根据flag更新父结点的左/右指针if(pre){flag ? (pre->right = current->right) : (pre->left = current->right);free(current);return tree;}else{BinTree tmp_right = current->right;free(current);return tmp_right;}}//该元素没有右孩子结点else if (current->right == NULL){if(pre){flag ? (pre->right = current->left) : (pre->left = current->left);free(current);return tree;}else{BinTree tmp_left = current->left;free(current);return tmp_left;}}//该元素有两个结点else{//寻找左子树的最右侧结点BinTree tmp = current->left;BinTree tmp_pre = NULL;while (tmp->right){tmp_pre = tmp;tmp = tmp->right;}//将最右侧结点的值替换掉要删除的结点的值，这样就不破坏原有结构current->data = tmp->data;//若左孩子结点就是左子树中最右侧的结点，则需要更新current的左指针，否则需要更新其父结点的右指针tmp_pre ? (tmp_pre->right = tmp->left) : (current->left = tmp->left);free(tmp);return tree;}
}

        还有一种压缩的考虑方法，是将上述的情况2和3合并了，只需要考虑两种情况：

        一是该结点没有左子树，此时直接提拔右子树。

        二是该结点有左子树，在上述的情况2中考虑的是没有右子树，则直接提拔左子树。本种情况的处理则是不管有没有右子树，都直接从左子树中挑最右侧结点进行替换，该情况下仍然要区分左子树的最右侧结点时的两种情况。

        下面对情况一二进行解释：

        一：此时若右子树存在，删除结点之后则只有右子树可以补上；即使右子树不存在，为NULL，相当于补上了一个空树，肯定不影响树的结构。

        二：此时若右子树存在，按之前的情况3来看，可以从左子树的最右侧和右子树在最左侧选择一个结点来替换，这里我选择的是左子树的最右侧结点，和之前的情况3重合，不再解释；此时若右子树不存在，按之前的情况2，可以直接将左子树补上，但是如果我们选择用左子树的最右侧结点来替换，结果也是正确的，因为最右侧结点就是树中元素的最大值，左子树的根结点肯定小于它，符合二叉搜索树的结构。

        所以合并之前的情况2,3的关键在于将情况2换了一种处理方法，使其和情况3的处理方法一致。

BinTree BinTree_delete(BinTree Tree,ElemType data)
{BinTree pre = NULL;        //当前结点的父结点，当前结点初始为根结点，所以父结点初始为NULLBinTree current = Tree;    //当前结点，初始为根结点int flag = 0;               //0代表当前结点是父结点的左孩子，1代表是右孩子//循环找到待删除结点while (current){if(data > current->data){pre = current;current = current->right;flag = 1;}else if(data < current->data){pre = current;current = current->left;flag = 0;}else//找到时跳出循环break;}//若不存在该结点，则返回原树if(current == NULL)return Tree;//若该结点没有左子树，则提拔右子树补齐if(current->left == NULL){//若待删除结点不是根结点则使父结点更新左/右指针if(pre){BinTree tmp = current;(flag == 1) ? (pre->right = current->right) : (pre->left = current->right);free(tmp);return Tree;}//若待删除结点是根结点则要返回新的根结点else{BinTree tmp = current->right;free(current);return tmp;}}//若该结点有左子树，则不管有没有右子树都从左子树中提取最右侧结点else{//保存待删除结点BinTree tmp = current;pre = current;current = current->left;//循环找到左子树的最右侧结点while (current->right){pre = current;current = current->right;}//替换掉待删除结点的数据域tmp->data = current->data;//若左子树只有一个结点，则需要更新待删除结点的左指针，其余情况更新父结点的右指针if(pre == tmp)pre->left = current->left;elsepre->right = current->left;//最右侧结点的数据已经替换了，所以该结点可以释放了free(current);return Tree;}
}