当前位置：首页 > news >正文

Python生成统计学公式

news 2025/8/8 5:44:17

一元线性回归模型
§2.1回归分析概述/25
一、回归分析基本概念/25
二、总体回归函数/27
三、随机误差项/29
四、样本回归函数/30
§2.2 一元线性回归模型的参数估计/32
一、参数估计的普通最小二乘法/32
二、拟合优度/35
§2.3基本假设与普通最小二乘估计量的统计性质/36
一、一元线性回归模型的基本假设/36
二、普通最小二乘估计量的统计性质/39
§2.4 一元线性回归模型的统计检验/42
一、参数估计量的概率分布及随机干扰项方差的估计/42
二、变量的显著性检验/43
三、参数检验的置信区间估计/45
§2.5 一元线性回归分析的应用：预测问题/46
一、预测值是条件均值或个别值的一个无偏估计/46
二、总体条件均值与个别值预测值的置信区间/47
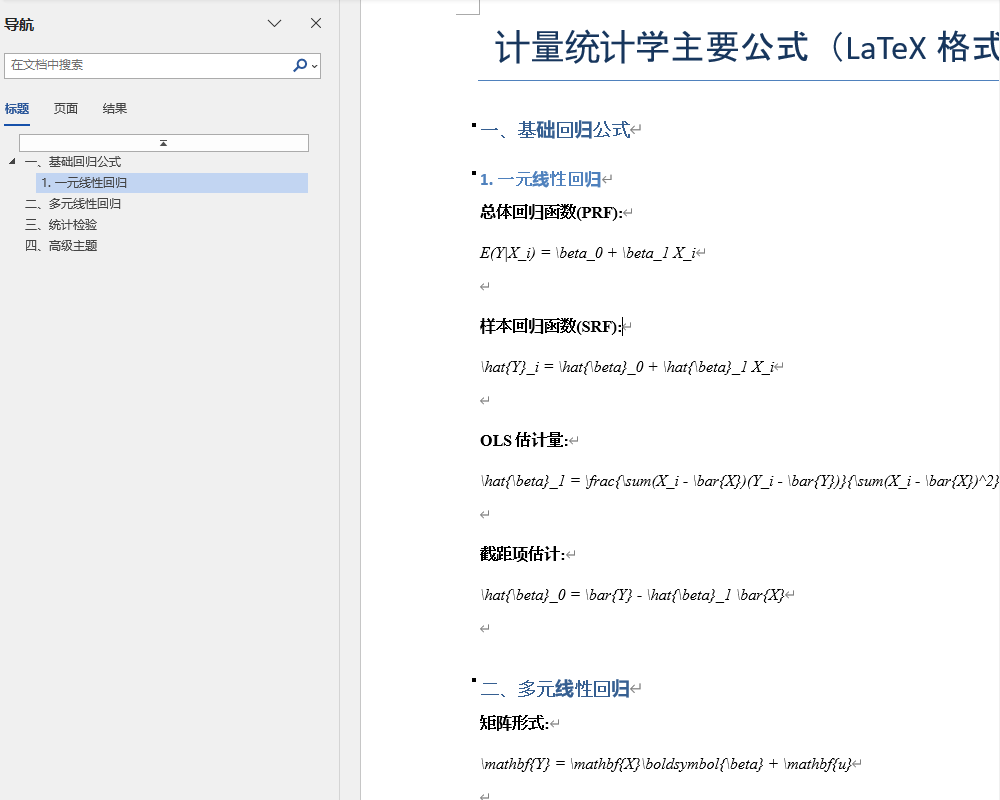
主要公式latex格式，word版

from docx import Document
from docx.shared import Pt
from docx.oxml import OxmlElement
from docx.oxml.ns import qndef create_formula_doc():doc = Document()# 设置文档默认字体style = doc.styles['Normal']font = style.fontfont.name = 'Times New Roman'font.size = Pt(12)# 添加标题title = doc.add_heading('计量统计学主要公式（LaTeX格式）', level=0)title.alignment = 1  # 居中# ================= 1. 基础回归公式 =================doc.add_heading('一、基础回归公式', level=1)# 1.1 一元线性回归doc.add_heading('1. 一元线性回归', level=2)add_formula(doc, '总体回归函数(PRF):', r'E(Y|X_i) = \beta_0 + \beta_1 X_i')add_formula(doc, '样本回归函数(SRF):', r'\hat{Y}_i = \hat{\beta}_0 + \hat{\beta}_1 X_i')add_formula(doc, 'OLS估计量:', r'\hat{\beta}_1 = \frac{\sum(X_i - \bar{X})(Y_i - \bar{Y})}{\sum(X_i - \bar{X})^2}')add_formula(doc, '截距项估计:', r'\hat{\beta}_0 = \bar{Y} - \hat{\beta}_1 \bar{X}')# ================= 2. 多元回归 =================doc.add_heading('二、多元线性回归', level=1)add_formula(doc, '矩阵形式:', r'\mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \mathbf{u}')add_formula(doc, 'OLS估计量:', r'\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{Y}')add_formula(doc, '方差协方差矩阵:', r'\text{Var}(\hat{\boldsymbol{\beta}}) = \sigma^2 (\mathbf{X}^\top \mathbf{X})^{-1}')# ================= 3. 统计检验 =================doc.add_heading('三、统计检验', level=1)add_formula(doc, 't检验统计量:', r't = \frac{\hat{\beta}_k}{se(\hat{\beta}_k)} \sim t(n-K)')add_formula(doc, 'F检验统计量:', r'F = \frac{(RSS_R - RSS_U)/q}{RSS_U/(n-K)} \sim F(q,n-K)')add_formula(doc, '拟合优度:', r'R^2 = 1 - \frac{RSS}{TSS}, \quad \bar{R}^2 = 1 - \frac{n-1}{n-K}(1-R^2)')# ================= 4. 高级主题 =================doc.add_heading('四、高级主题', level=1)add_formula(doc, 'White异方差稳健标准误:', r'\text{Var}_{robust}(\hat{\boldsymbol{\beta}}) = (\mathbf{X}^\top \mathbf{X})^{-1} \left( \sum e_i^2 \mathbf{x}_i \mathbf{x}_i^\top \right) (\mathbf{X}^\top \mathbf{X})^{-1}')add_formula(doc, '最大似然估计:', r'\ln L(\boldsymbol{\theta}) = \sum \ln f(Y_i | \mathbf{X}_i; \boldsymbol{\theta})')add_formula(doc, 'AR(1)模型:', r'Y_t = \rho Y_{t-1} + \varepsilon_t, \quad |\rho| < 1')# 保存文档doc.save('计量统计学公式.docx')print("Word文档已生成：计量统计学公式.docx")def add_formula(doc, description, latex_formula):"""添加带描述的公式到Word文档"""# 添加描述文本p = doc.add_paragraph()p.add_run(description).bold = True# 添加LaTeX公式（实际使用时需转换为Word公式对象）# 这里使用简单文本模拟，实际应使用LaTeX转Word公式工具formula = doc.add_paragraph()formula.add_run(latex_formula).italic = True# 添加空行doc.add_paragraph()if __name__ == "__main__":create_formula_doc()