车间调度|基于帝王蝶优化算法的车间调度(Matlab代码实现)
目录
1 概述
2 蝴蝶优化算法
3 车间调度
3.1 车间调度描述
3.2 数学模型
4 运行结果
5 参考文献
6 Matlab代码实现
1 概述
随着智能化在制造业中的普及,解决车间生产调度的问题能有效提高车间的工作学习效率,实现车间现场管理的有序化、智能化和高效化。为了合理地协调控制各个机器的生产以实现多方面目标的 pareto最优状态,学者们经过多年的研究,使用各种不同的方法来分析和解决生产环节的FJSP。
随着研究的逐渐深入,为了更贴近车间生产现场的工作状态,人们将柔性车间这一概念与车间调度问题相融合并提出了FJSP。由于FJSP问题在生产中广泛存在,因此,该问题引起了国内外相关学者的广泛关注与研究"5'。IshibuchiH使用遗传算法求解FJSP问题,但算法的有效性较低l6'。Deng Q W使用NSGA-II算法并考虑分两阶段对多目标FJSP进行求解,并通过一些常用的函数验证算法的准确性。Kaya S 导人入lI新管法的思想解决以完工分析了多目例上S是小和瓶颈工序负荷最小为目时间最大、机器负荷最小和瓶颈工序负荷最小为目标的FJSP问题。
2 蝴蝶优化算法
| 基于帝王蝶算法MBO求解最优目标(Matlab完整代码实现) |
3 车间调度
3.1 车间调度描述
作业车间调度是根据实际车间有限的可用资源和已定的生产计划,在满足工艺约束的基础上合理安排生产路线,均衡生产负荷,完成生产计划的同时实现某种既定目标的问题。FJSP是为了解决作业车间调度如何才能与多台并行机相结合而提出的,主要涉及以下两个问题:
(1)按什么顺序加工工件。
(2)如何合理地分配机器。
FJSP已被证明是更复杂的NP-hard问题,本文的FJSP问题主要是基于解决以上2个问题,并结合车间的实际生产为了达到完成时间最短和总流程时间最短的目标求出的pareto最优解。
FJSP可以用以下例子来描述:设车间有m台机器,需要加工n个工件,每台机器表示为M,
M,。每个工件表示为N, N2,…., Nn。每个工件在机器上一次性完成的工艺过程叫工序,表示工件i的第j道工序。最终的目标是使完成这批工件所用的时间最短和消耗的能源最少。相关的约束条件有:
( 1)一台机器在某一时刻只加工一个工件。
(2)每个工件加工生产的工序相同,工序的加工顺序相同,根据算例的不同,不同工件在不同机器上加工消耗的时间不同。
(3)相同工件在某一时刻不能被不同的两台机器加工。
( 4)工件在加工过程中不能更换机器加工。经典的FJSP 如下所示。以5台机器加工3个工件,每个工件有3个加工工序的情况为例,加工的时间表如表1所示。
3.2 数学模型

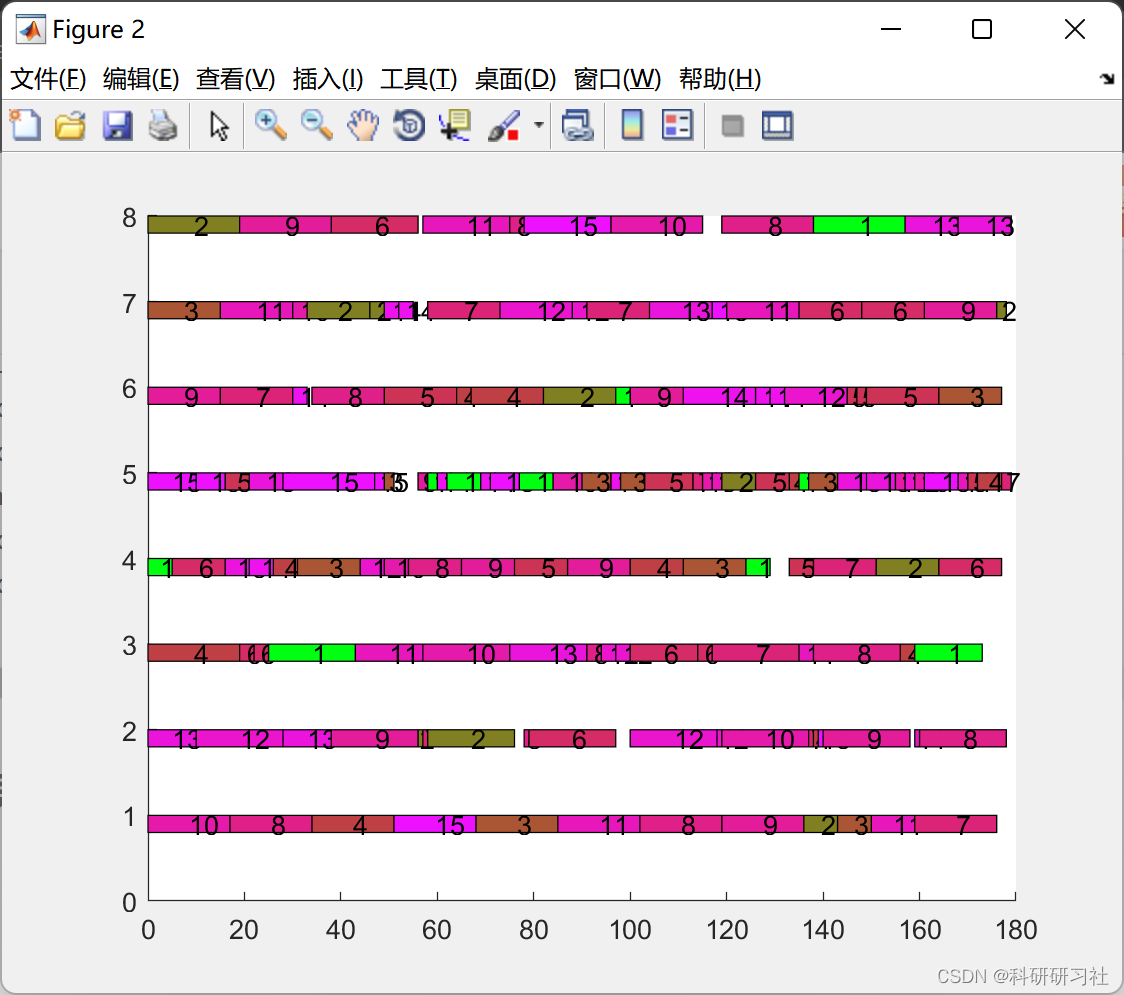
4 运行结果


5 参考文献
部分理论引用网络文献,如有侵权请联系删除。
[1]杨红雄,王惠酩.麻雀搜索算法解决柔性作业车间调度问题[J].制造技术与机床,2022(7):158-164
[2]郑洪清,冯文健,周永权.融合正弦余弦算法的蝴蝶优化算法[J].广西科学,2021,28(2):152-159
6 Matlab代码实现
博客主页:@橘柑橙柠桔柚
