算法11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

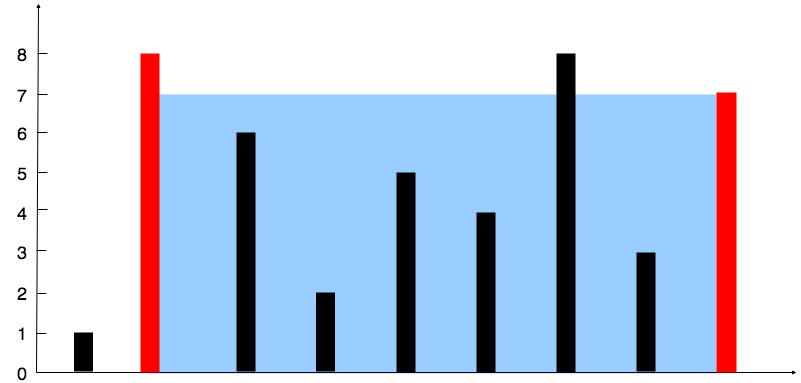
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

class Solution:# 双指针做法def maxArea(self, height: List[int]) -> int:max_area=0left = 0right = len(height) -1 while left < right:area = min(height[left],height[right])*(right-left)max_area = max(max_area,area)if height[left]<height[right]:left+=1else:right-=1return max_area

🧠 为什么移动较矮的一边？

我们来思考一个问题：

当前 left 和 right 构成一个容器。
如果我们移动一个指针，另一个不动，哪边移动后有可能得到更大的面积？

假设：height[left] < height[right] → 移动 left

• 当前高度由 height[left] 决定（短板）
• 如果我们移动 right 向内：
  • 宽度一定变小（right - left 减小）
  • 高度最多还是 height[left]（因为左边没变）
  • 所以面积一定 ≤ 当前面积（甚至更小）
• 但如果我们移动 left 向内：
  • 宽度变小，但新的 height[left] 可能更高，从而提升整体高度
  • 有可能得到更大的面积

✅ 所以：只有移动较矮的一边，才有可能获得更大的面积

移动较高的那一边，宽度减小，高度不会增加（仍受短板限制），面积只会更小或不变。