算法-CodeTop(三)
7整数反转
题目
思路解析
溢出条件有两个,一个是大于整数最大值MAX_VALUE,另一个是小于整数最小值 MIN_VALUE
设当前计算结果为 ans,下一位为 pop
从 ans * 10 + pop > MAX_VALUE 这个溢出条件来看:
- 当出现 ans > MAX_VALUE / 10 且 还有pop需要添加 时,则一定溢出
- 当出现 ans == MAX_VALUE / 10 且 pop > 7 时,则一定溢出,7 是 2^31 - 1 的个位数
从 ans * 10 + pop < MIN_VALUE 这个溢出条件来看:
- 当出现 ans < MIN_VALUE / 10 且 还有pop需要添加 时,则一定溢出
- 当出现 ans == MIN_VALUE / 10 且 pop < -8 时,则一定溢出,8 是-2^31 的个位数
最大值 MAX_VALUE:2^31 - 1,计算结果为 2147483647,其个位数是7
最小值 MIN_VALUE:-2^31,计算结果为 -2147483648,其个位数是8(忽略负号时)
代码
class Solution {public int reverse(int x) {int ans = 0;while (x != 0) {int pop = x % 10;if (ans > Integer.MAX_VALUE / 10 || (ans == Integer.MAX_VALUE / 10 && pop > 7)) return 0;if (ans < Integer.MIN_VALUE / 10 || (ans == Integer.MIN_VALUE / 10 && pop < -8)) return 0;ans = ans * 10 + pop;x /= 10; }return ans;}
}
LCR 187 破冰游戏
题目
思路解析
这个问题是约瑟夫问题
N个人围成一圈,第一个人从1开始报数,报M的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,求最后的胜利者
我们只需要关注最后存活人的下标的变化,最后存活人的在最后的下标一定是0
LCR 187. 破冰游戏 - 力扣(LeetCode)
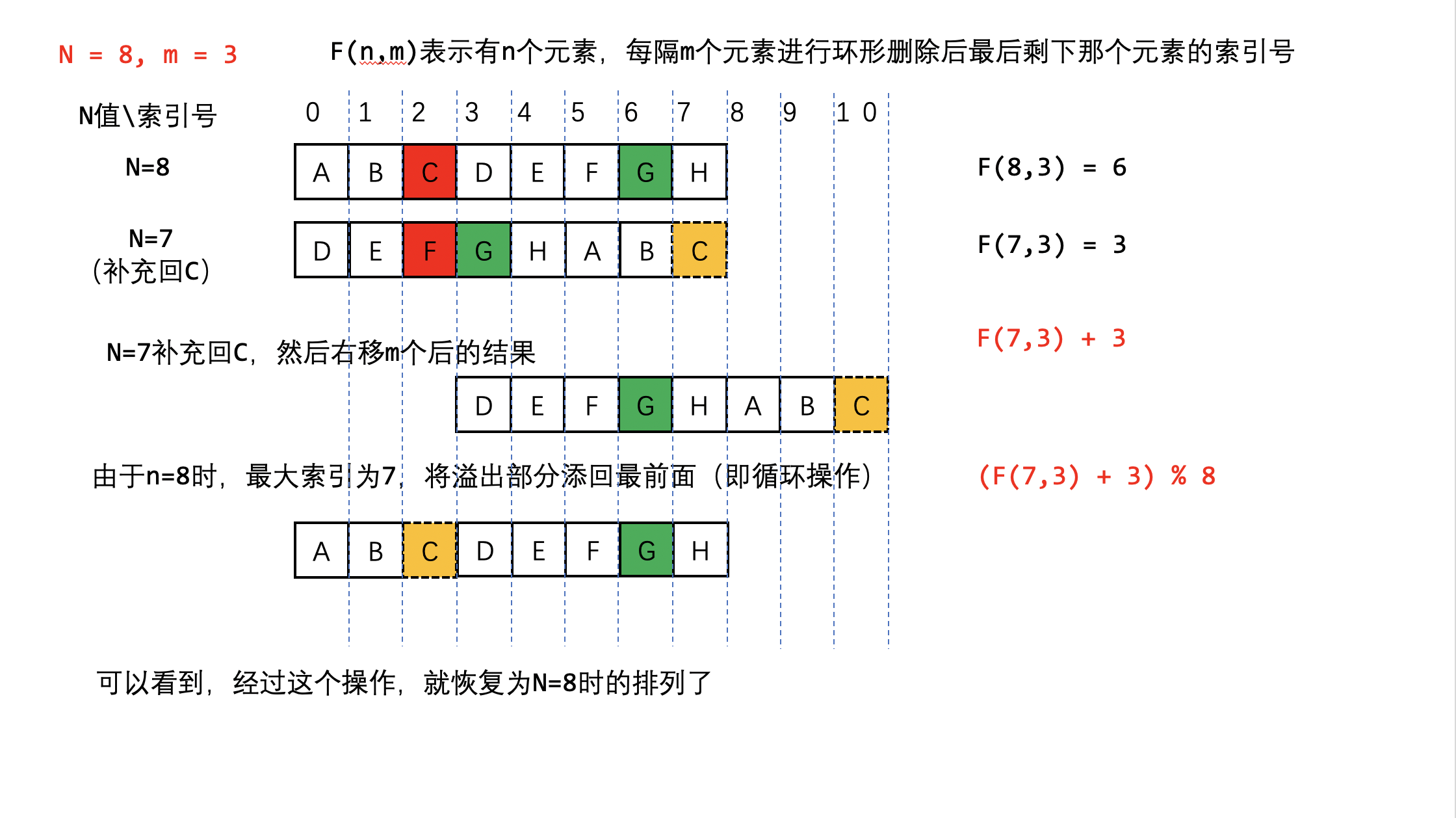
因此我们可以推出递推公式f(8,3)=[f(7,3)+3]%8
进行推广泛化,即f(n,m)=[f(n−1,m)+m]%n
直接从0开始倒推
代码
class Solution {public int iceBreakingGame(int num, int target) {int x = 0;for (int i = 2; i <= num; i++) {x = (x + target) % i;}return x;}
}LCR 139 训练计划 I
题目
思路解析
快慢指针,每次碰到fast指针碰到奇数就和low指针的元素交换位置
代码
class Solution {public int[] trainingPlan(int[] actions) {int low = 0, fast = 0;while (fast < actions.length) {// 若当前元素是奇数,与low位置元素交换,并移动low指针if ((actions[fast] & 1) == 1) {int temp = actions[low];actions[low] = actions[fast];actions[fast] = temp;low++;}// 无论是否交换,fast指针始终向后移动fast++;}return actions;}
}LCR 126 斐波那契数
题目
思路解析
动态规划
代码
dp【】数组动态规划
class Solution {public int fib(int n) {if(n == 0) return 0;int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i-1] + dp[i-2];dp[i] %= 1000000007;}return dp[n];}
}空间复杂度优化
class Solution {public int fib(int n) {int a = 0;int b = 1;int sum;for(int i = 0; i < n; i++){sum = (a + b) % 1000000007;a = b;b = sum;}return a;}
}1047 删除字符串中的所有相邻重复项
题目
思路解析
利用栈,先放进去,遇到相同的则弹出
代码
class Solution {public String removeDuplicates(String s) {ArrayDeque<Character> deque = new ArrayDeque<>();for (int i = 0; i < s.length(); i++) {if (deque.size() == 0 || deque.peek() != s.charAt(i)) {deque.push(s.charAt(i));} else {deque.pop();}}StringBuilder str = new StringBuilder();while (!deque.isEmpty()) {str.insert(0, deque.pop());}return str.toString();}
}163 Excel 表列名称
题目
思路解析
这是一道从 1 开始的的 26 进制转换题
对于一般性的进制转换题目,只需要不断地对 columnNumber 进行 % 运算取得最后一位
然后对 columnNumber 进行 / 运算,将已经取得的位数去掉,直到 columnNumber 为 0 即可
一般性的进制转换题目无须进行额外操作
这是因为我们是在「每一位数值范围在 [0,x)」的前提下进行「逢 x 进一」
但本题需要我们将从 1 开始,因此在执行「进制转换」操作前,我们需要先对 columnNumber 执行减一操作,从而实现整体偏移
(char)(cn % 26 + 'A')代码
class Solution {public String convertToTitle(int cn) {StringBuilder sb = new StringBuilder();while (cn > 0) {cn--;sb.append((char)(cn % 26 + 'A'));cn /= 26;}sb.reverse();return sb.toString();}
}
459 重复的子字符串
题目
思路解析
假设字符串 s 真的是由某个子串重复组成的,比如 s = "abcabc",它的重复子串是 "abc",重复了 2 次
那 s + s 就是 "abcabcabcabc"。现在看这个拼接后的字符串
我们去掉第一个字符和最后一个字符,得到 "bcabcabca"
你会发现,"abcabc"(也就是原始的 s)就藏在这个新串里 —— 从第 2 个字符到第 7 个字符就是它
再换个例子,s = "ababab",重复子串是 "ab",重复了 3 次
s + s 是 "abababababab",去掉首尾字符后是 "bababababa",这里面显然能找到 "ababab"
为什么会这样?
因为当 s 由子串 t 重复 n 次组成时(s = t×n),s + s 就等于 t×n + t×n
这时候,只要从第一个 t 的第二个字符开始截取,就能在中间部分找到一个完整的 t×n(也就是 s)
比如 "abcabc"+"abcabc" 变成 "abcabcabcabc",从第二个字符开始的 "bcabcabcab" 里,就包含 "abcabc"
反过来,如果 s 不能由重复子串组成,比如 s = "abcd",那么 s + s = "abcdabcd",去掉首尾后是 "bcdabc",这里面根本找不到 "abcd"
所以这个方法的逻辑是:如果 s 是重复子串组成的,那么 s+s 掐头去尾后一定包含 s
反之则不包含
关键步骤分析
- 字符串拼接:String str = s + s;
将原字符串 s 复制一份并拼接在后面,形成新字符串 str - 子串截取:str.substring (1, str.length () - 1)
截取 str 的中间部分(去掉第一个字符和最后一个字符)
这样可以排除 s 作为前缀或后缀的情况 - 包含判断:.contains (s)
检查截取的中间部分是否包含原始字符串 s
如果包含,则说明 s 可以由某个子串重复组成
代码
优雅代码
class Solution {public boolean repeatedSubstringPattern(String s) {String str = s + s;return str.substring(1, str.length() - 1).contains(s);
}
}
暴力代码
如果s由重复子串t组成(即s = t×n),那么:
- 循环右移 k 位(k 是 t 的长度的倍数)相当于把前 m 个 t 移到后面
- 这不会改变字符串的周期性,因此移位后的字符串仍等于原字符串
这个算法的时间复杂度是 O (n²),因为需要尝试 n-1 次移位,每次移位需要 O (n) 时间。虽然不是最优解,但它提供了一个直观且有效的判断方法。
class Solution {
public boolean repeatedSubstringPattern(String s) {for(int i = 1; i < s.length(); i++) {String str = rotate(s.toCharArray(),i);if(s.equals(str)) return true;}return false;}public String rotate(char[] nums, int k) {k = k % nums.length;reverse(nums, 0, nums.length - 1);reverse(nums, 0, k - 1);reverse(nums, k, nums.length - 1);return String.valueOf(nums);}public void reverse(char[] nums, int begin, int end) {int i = begin, j = end;while(i < j) {char temp = nums[i];nums[i++] = nums[j];nums[j--] = temp;}}
}