当前位置： 首页 > news >正文

对College数据进行多模型预测(R语言)

news 2025/7/30 8:25:14

目录

一、目的

二、数据准备

1、数据加载并分析

1.1 变量解读

2、创建训练集和测试集

三、建模

1. 回归模型

1.1线性回归

 1.1.4 处理多重共线性的方法

1.2逐步回归

1.3岭回归

​编辑

1.4LASSO回归

1.5 Elastic Net回归

2.树模型

2.1决策树

2.2随机森林

2.3 梯度提升模型 XGBoost 

3.降维

3.1 主成分回归 PCR = PCA + 回归

3.2 偏最小二乘回归 PLS

 四、模型比较

一、目的

利用R语言对ISLR包中的College数据的Apps列进行预测

二、数据准备

1、数据加载并分析

library(ISLR)
college <- College
head(college)
# 查看data类型
str(college)# 检查是否有缺失数据(无data缺失)
library(VIM)
aggr(college,prop=F,numbers=T)

1.1 变量解读

变量含义
PrivateYes私立学校or公立学校
Accept被录取者
Enroll实际入学者
Top10perc学生中前 10% 的比例
Top25perc学生中前 25% 的比例
F.Undergrad全日制本科生
P.Undergrad非全日制本科生
Outstate州外学费
Room.Board食宿费用
Books书本费
Personal其他个人支出
perc.alumni有多少比例的校友向母校捐款
Expend每位学生支出
Grad.Rate毕业率

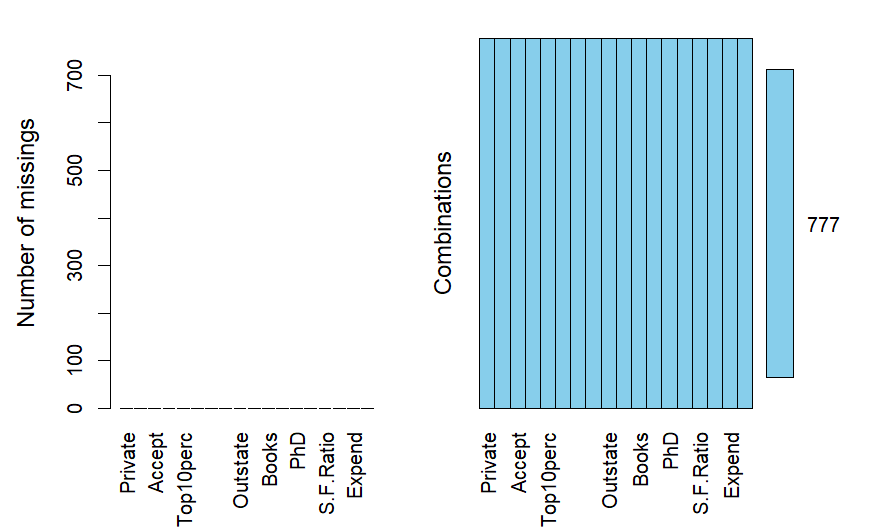
分析：1.由上图可知，各变量数据完整

        2. Apps 为申请人数，为连续型数值变量，所以后续可以做回归 

2、创建训练集和测试集

set.seed(123) # 设置随机种子使实验结果可重复性
# 取70%为训练集
ind <- sample(1:nrow(college),nrow(college)* .7)
train <- college[ind,]
test <- college[-ind,]

三、建模

1. 回归模型

# reason: 目标变量（特征变量）是连续性数值变量 ；自变量很丰富 ； 两者存在潜在的线性 or 非线性关系
# ATTN: 当存在变量之间的多重共线性问题(变量高度相关) 则可以引入岭回归/LASSO模型
# Q1: 如何感性和理性判断变量之间存在多重共线性问题？
# Q2: 如何解决变量之间存在的多重共线性问题？
# Q2+: 岭回归/LASSO回归 为什么可以解决多重共线性问题，优势在哪？

1.1线性回归

1.1.1 建模

lm <- lm(Apps ~ .,data = train)
summary(lm)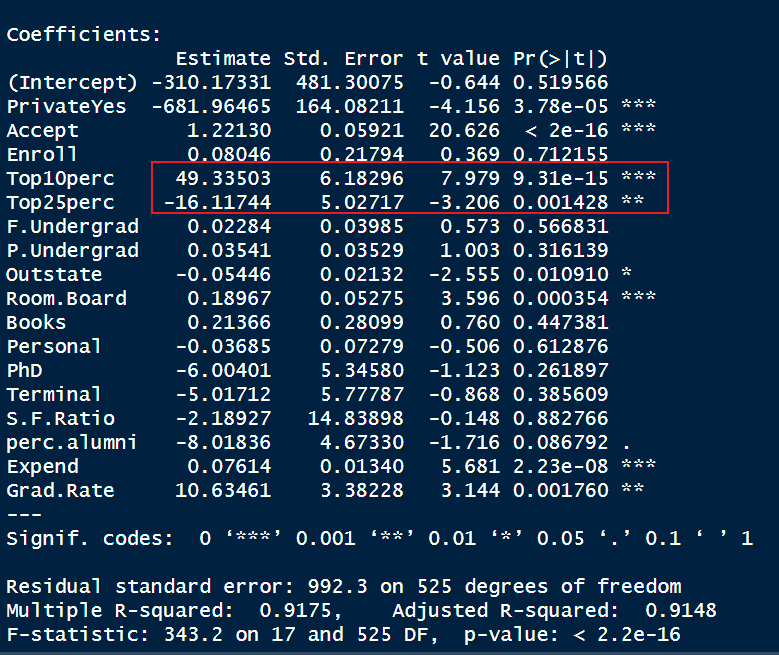

我们知道Top10prec 和Top25prec为 相同性质的参数，应该对apps均为正向作用，但是上述回归模型却表现出相反的效果，由此可以存在着多重共线性问题

1.1.2预测&评价

pred_lm <- predict(lm,newdata = test)
mse_lm <- mean( (pred_lm - test$Apps) ^ 2) 
mse_lm # 均方误差MSE 1734841
rmse_lm <- sqrt(mean((pred_lm-test$Apps)^2))
rmse_lm # 均方根误差 1317.134
mae_lm <- mean(abs(pred_lm - test$Apps))
mae_lm # 平均绝对误差 644.1637

1.1.3判断是否存在多重共线性

1.1.3.1利用相关系数

if > 0.8,则表示存在多重共线性，根据相关系数不同进行分类，从而可以直观看到

# 相关系数矩阵
cor_matrix <- cor(college[,sapply(college,is.numeric)],use = "complete.obs")symbolize_cor <- function(r) {ifelse(abs(r) >= 0.8, "★★★",ifelse(abs(r) >= 0.3, "★★",ifelse(abs(r) >= 0.1, "★", "○")))
}# 3. 生成符号化矩阵
symbol_matrix <- apply(cor_matrix, c(1,2), symbolize_cor)
diag(symbol_matrix) <- "-"  # 对角线设为"-"symbol_matrix
library(ggplot2)
library(reshape2)
melted_cor <- melt(cor_matrix) ggplot(melted_cor, aes(Var1, Var2, fill = value)) + geom_tile(color = "white") +geom_text(aes(label = symbolize_cor(value)), size = 4) +   scale_fill_gradient2(low = "blue", high = "red", mid = "white", midpoint = 0, limit = c(-1,1), name = "Correlation") +theme_minimal() +theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1)) +coord_fixed()

结果：

 

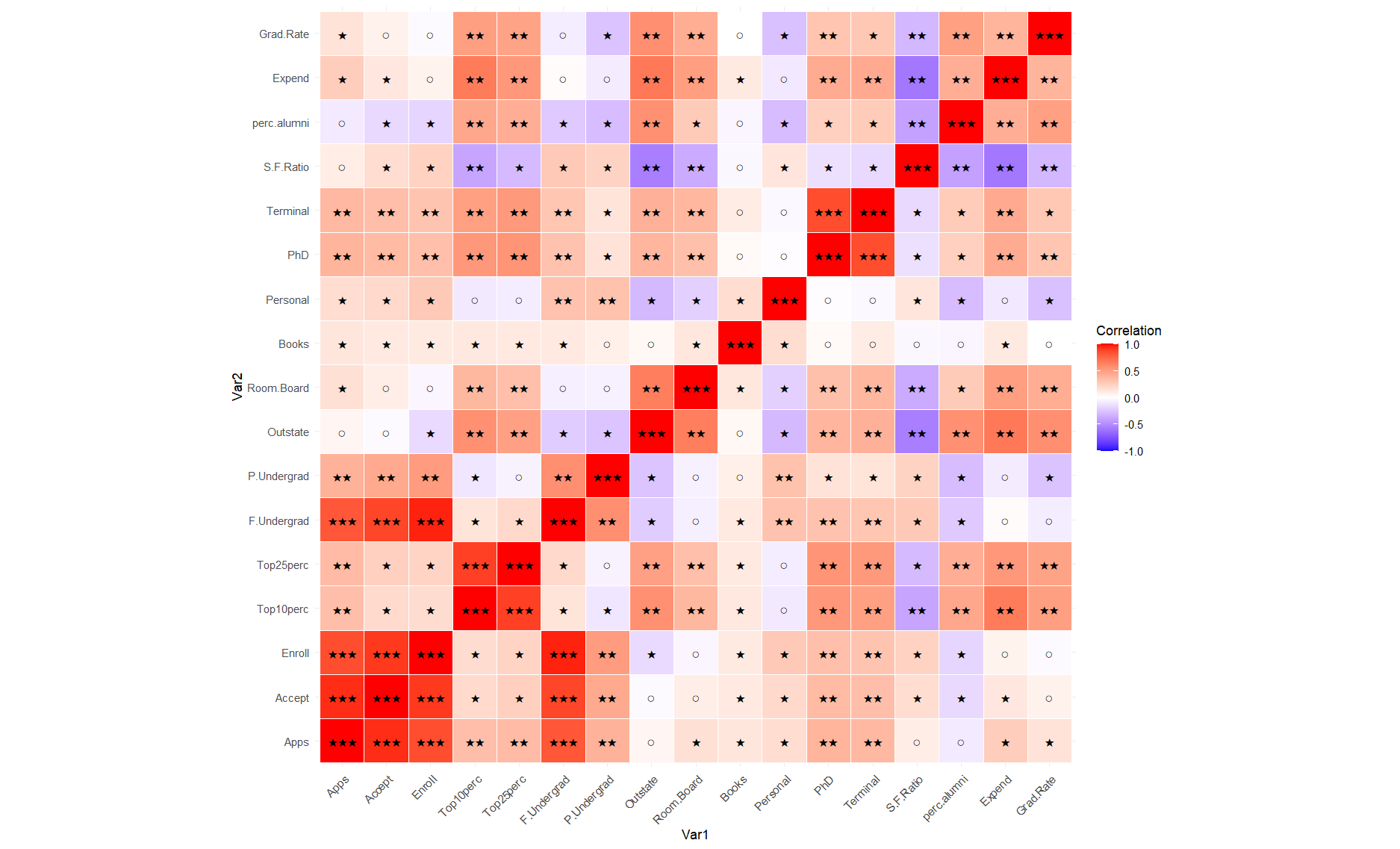
由非对角线上三星的可知强相关： F & Accept 、F & enroll 、Top10 & Top25 、 Enroll & Accept

1.1.3.2 方差膨胀因子（VIF）

VIF 值区间解读
1 ~ 5基本无多重共线性问题，可接受 ✅
5 ~ 10有中等共线性，需注意 ⚠️
> 10共线性严重，建议处理 ❌
# VIF
library(car)
model <- lm(Apps ~ ., data = college)
vif(model)

由此可知：# 严重：Enroll、F  中等：Top10 、Top25、Accept 

 1.1.4 处理多重共线性的方法

思想        方法
正则化
                		LASSO回归
岭回归
Elastic Net 回归
降维PCR
PLS

dis ： 正则化 vs 降维

正则化是用惩罚系数使某些变量不起作用，但是变量还在

降维是直接去掉某些变量

1.2逐步回归

if不知道如何处理多重共线性，那么可先用逐步回归进行降维，时选择回归模型中变量的自动方法，目标是寻找最优子集模型

1.2.1 AIC 和 BIC（模型选择准则） 

AIC（Akaike 信息准则）

AIC = 2 𝑘 − 2 ln ⁡ ( 𝐿 )

BIC（贝叶斯信息准则）

BIC = ln(n)k − 2ln(L)

通过aic或者bic 指标进行逐步回归模型的建立，之后选择aic 和 bic 最小值的模型即可

library(ISLR)
# 拟合全模型
full_model <- lm(Apps ~ ., data = college)
# 空模型（仅包含截距）
null_model <- lm(Apps ~ 1, data = train)
# 逐步回归（默认使用 AIC）
step_model_aic <- step(null_model,scope=list(lower = null_model, upper = full_model), direction = "both", trace = FALSE)
summary(step_model_aic) # .9154 
# 设置 BIC = AIC + log(n) * k - 2logL
n <- nrow(college)
step_model_bic <- step(full_model, direction = "both", k = log(n), trace = FALSE)
summary(step_model_bic) # 0.9274 # 输出 AIC 与 BIC 值进行比较
cat("AIC比较：\n")
cat("Full Model AIC:", AIC(full_model), "\n") # 13022.43
cat("Stepwise Model AIC:", AIC(step_model_aic), "\n") # 9044.535
cat("Stepwise Model BIC:", AIC(step_model_bic), "\n") # 13018.01cat("BIC比较：\n")
cat("Full Model BIC:", BIC(full_model), "\n") # 13110.88
cat("Stepwise Model AIC:", BIC(step_model_aic), "\n") # 9100.397
cat("Stepwise Model BIC:", BIC(step_model_bic), "\n") # 13073.87# 在测试集上预测
pred_full <- predict(full_model, newdata = test)
pred_step_aic <- predict(step_model_aic, newdata = test)
pred_step_bic <- predict(step_model_bic, newdata = test)# 计算 RMSE
rmse_full <- sqrt(mean((pred_full - y_test)^2))
rmse_step_aic <- sqrt(mean((pred_step_aic - y_test)^2))
rmse_step_bic <- sqrt(mean((pred_step_bic - y_test)^2))cat(sprintf("完整模型 RMSE: %.2f\n", rmse_full)) # 1056.23
cat(sprintf("AIC标准逐步回归模型 RMSE: %.2f\n", rmse_step_aic)) # 1309.17
cat(sprintf("BIC标准逐步回归模型 RMSE: %.2f\n", rmse_step_bic)) # 1077.85

由此可知参数最佳模型为step_model_aic,但是在拟合度上仍低于拟合全模型

1.3岭回归

library(glmnet)
# 1.数据准备  
# 将所有解释变量转为 数值矩阵 
x_train <- model.matrix(Apps ~ ., train)[, -1] # [, -1]:glmnet 自动会加上 intercept
x_test <- model.matrix(Apps ~ ., test)[, -1]
y_train <- train$Apps
y_test <- test$Apps# 2.建模 & 交叉验证选择 λ（惩罚参数）
ridge_mod <- glmnet(x_train, y_train, alpha = 0)#  alpha = 0表示岭回归； alpha = 1 则是 Lasso 回归
cv_ridge <- cv.glmnet(x_train, y_train, alpha = 0) # cv.glmnet使用 交叉验证（默认 10 折） 来选择最佳的 lambda。
best_lambda_ridge <- cv_ridge$lambda.min # lambda.min 是使交叉验证误差最小的那个 lambda，即最佳惩罚强度。plot(ridge_mod, xvar = "lambda", label = TRUE)
title("岭回归 系数路径图") # 3.预测与评估模型
pred_ridge <- predict(ridge_mod,s = best_lambda_ridge,newx = x_test)
mse_ridge <- mean((pred_ridge - y_test) ^ 2)
mse_ridge  # 2976365
rmse_ridge <- sqrt(mean((pred_ridge - y_test) ^ 2))
rmse_ridge # 1725.214

1.4LASSO回归

# LASSO 回归
library(glmnet)
# 1.数据准备 （同上） 
x_train <- model.matrix(Apps ~ ., train)[, -1] 
x_test <- model.matrix(Apps ~ ., test)[, -1]
y_train <- train$Apps
y_test <- test$Apps# 2.建模 & 交叉验证选择min lambda
lasso_mod <- glmnet(x_train,y_train,alpha = 1)
cv_lasso <- cv.glmnet(x_train,y_train,alpha = 1)
best_lambda_lasso <- cv_lasso$lambda.min# # 画出 LASSO 系数路径图
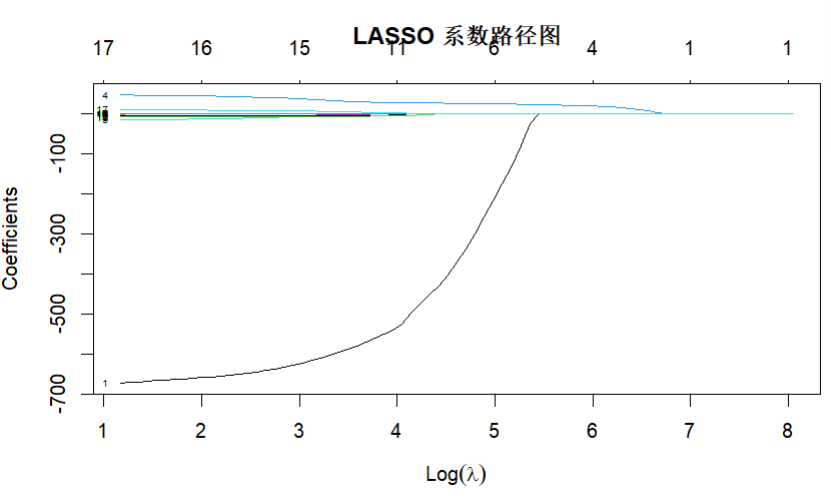
plot(lasso_mod, xvar = "lambda", label = TRUE)
title("LASSO 系数路径图")# 预测与评估模型
pred_lasso <- predict(lasso_mod,s = best_lambda_lasso,newx = x_test)
mse_lasso <- mean((pred_lasso - y_test) ^ 2)
mse_lasso # 1730981
rmse_lasso <- sqrt(mse_lasso)
rmse_lasso # 1315.667

1.5 Elastic Net回归

#  Elastic Net 回归分析(结合了 Ridge（L2 正则）和 LASSO（L1 正则）的一种回归方法)
elastic_mod <- glmnet(x_train, y_train, alpha = 0.5)
cv_elastic <- cv.glmnet(x_train, y_train, alpha = 0.5)
best_lambda_elastic <- cv_elastic$lambda.min
pred_elastic <- predict(elastic_mod, s = best_lambda_elastic, newx = x_test)
mse_elastic <- mean((pred_elastic - y_test)^2)
mse_elastic # 1784335
rmse_elastic <- sqrt(mse_elastic)
rmse_elastic # 1335.79

上述代码是将 Lasso 和 ridge 做相同权重进行的回归分析，但是我们可知最优的情况下Lasso 和 ridge 权重不一定相等

#  调整 alpha 和 lambda
# 设置 alpha 值的搜索范围
alpha_values <- seq(0, 1, by = 0.1)  # 从 0 到 1，步长为 0.1# 初始化用于记录最优结果的变量
best_mse <- Inf
best_alpha <- NA
best_lambda <- NA# 遍历每个 alpha，使用 cv.glmnet 找 lambda.min
for (a in alpha_values) {set.seed(123)  # 保持可重复性cv_model <- cv.glmnet(x_train, y_train, alpha = a, nfolds = 10)# 取交叉验证得到的最优 lambdalambda_min <- cv_model$lambda.min# 用当前模型对测试集进行预测pred <- predict(cv_model, s = lambda_min, newx = x_test)# 计算测试集 MSEmse <- mean((pred - y_test)^2)# 打印每个 alpha 的结果（可选）cat("alpha =", a, "| lambda.min =", round(lambda_min, 4), "| test MSE =", round(mse, 2), "\n")# 更新最优参数if (mse < best_mse) {best_mse <- msebest_alpha <- abest_lambda <- lambda_min}
}# 输出最终结果
cat("\n✅ 最优 alpha:", best_alpha,  # 1"\n✅ 最优 lambda:", best_lambda,  # 6.168902"\n✅ 最小测试集 MSE:", round(best_mse, 2), "\n") # 1730913# 用最优参数重新训练模型
final_model <- glmnet(x_train, y_train, alpha = best_alpha)
final_pred <- predict(final_model, s = best_lambda, newx = x_test)
final_mse <- mean((final_pred - y_test)^2)
cat("\n📌 使用最优参数的 Elastic Net 模型最终测试集 MSE:", round(final_mse, 2), "\n") # 1730913 
final_rmse <- sqrt(final_mse)
final_rmse # 1315.642

 由此可知，当alpha = 1时即 Lasso回归时 rmse min

2.树模型

非线性模型

2.1决策树

# 1.决策树模型（rpart）
library(rpart)
library(rpart.plot)tree_model <- rpart(Apps ~ ., data = train,method = "anova")
rpart.plot(tree_model)pred_tree <- predict(tree_model,newdata = test)
mse_tree <- mean((pred_tree - y_test) ^ 2)
mse_tree
rmse_tree <- sqrt(mse_tree)
rmse_tree # 2479.202

2.2随机森林

# 2.随机森林 
library(randomForest)
set.seed(123)
rf_model <- randomForest(Apps ~ .,data = train,importance = T,ntree = 500)pred_rf <- predict(rf_model, newdata = test)
mse_rf <- mean((pred_rf - y_test)^2)
mse_rf
rmse_rf <- sqrt(mse_rf)
rmse_rf # 2348.264

2.3 梯度提升模型 XGBoost 

# 梯度提升模型 XGBoost
library(xgboost)# 将数据转化为 xgboost 可用格式
x_train <- model.matrix(Apps ~ ., train)[, -1]
x_test <- model.matrix(Apps ~ ., test)[, -1]
y_train <- train$Apps
y_test <- test$Appsdtrain <- xgb.DMatrix(data = x_train, label = y_train)
dtest <- xgb.DMatrix(data = x_test, label = y_test)# 训练模型
set.seed(123)
xgb_model <- xgboost(data = dtrain,nrounds = 100, # 迭代次数max_depth = 6,eta = 0.1, # 学习率subsample = 0.8, # 行采样比率colsample_bytree = 0.8, # 列采样比率objective = "reg:squarederror", # 损失函数verbose = 0 # 是否显示训练过程信息
)# nrounds 迭代次数（boosting rounds），也就是训练多少棵树（弱学习器）。太小可能欠拟合，太大可能过拟合。# objective 损失函数，这里使用平方误差（最小化 MSE），适用于回归问题。# verbose 是否显示训练过程信息，0 表示不显示，1 或 2 会打印更多训练进度。# 预测与评估
pred_xgb <- predict(xgb_model, newdata = dtest)
mse_xgb <- mean((pred_xgb - y_test)^2)
print(paste("XGBoost MSE:", round(mse_xgb, 2)))
rmse_xgb <- sqrt(mse_xgb)
rmse_xgb # 2151.398

上述参数是用常用的一组参数组进行的梯度提升模型的训练，但是并非为最优参数组

# 确定最优参数组： caret + 网格搜索 自动调参
library(caret)# 参数组合网格
xgb_grid <- expand.grid(nrounds = c(100, 200, 300),max_depth = c(3, 5, 7),eta = c(0.01, 0.05, 0.1),gamma = 0,          # 可选：控制剪枝，越大越保守colsample_bytree = c(0.7, 0.9),min_child_weight = 1,subsample = c(0.7, 0.9)
)# 交叉验证设置
ctrl <- trainControl(method = "cv", number = 5)# 模型训练 + 自动调参
xgb_tuned <- train(x = x_train, y = y_train,method = "xgbTree",trControl = ctrl,tuneGrid = xgb_grid,verbose = FALSE
)# 输出最优参数组合
xgb_tuned$bestTune

调用最优参数组进行模型训练

final_model <- xgboost(data = dtrain,nrounds = xgb_tuned$bestTune$nrounds, max_depth = xgb_tuned$bestTune$max_depth,eta = xgb_tuned$bestTune$eta,subsample = xgb_tuned$bestTune$subsample,colsample_bytree = xgb_tuned$bestTune$colsample_bytree,min_child_weight = xgb_tuned$bestTune$min_child_weight,objective = "reg:squarederror",verbose = 0
)# 在测试集上预测
pred_xgb <- predict(final_model, newdata = dtest)
final_mse_xgb <- mean((pred_xgb - y_test)^2)
cat("最终 XGBoost 测试集 MSE:", round(mse_xgb, 2), "\n")
final_rmse_xgb <- sqrt(final_mse_xgb)
final_rmse_xgb # 2042.134

3.降维

3.1 主成分回归 PCR = PCA + 回归

library(pls)
# PCR 建模： 内部已经做了PCA
pcr_model <- pcr(Apps ~ ., data = train, scale = T,  # scale = TRUE：对每个变量标准化（均值为0，方差为1），避免量纲影响validation = "CV") # 使用交叉验证（Cross Validation）来评估模型性能

在进行预测时需要确定主成分个数，因此需要确定最佳主成分个数

注意 ：个数不能太少（1~2个） 容易欠拟合；个数不能太多（接近原来个数） 容易过拟合

validationplot(pcr_model, val.type = "MSEP",main = "PCR - CV MSE vs 主成分数") # 绘制验证图


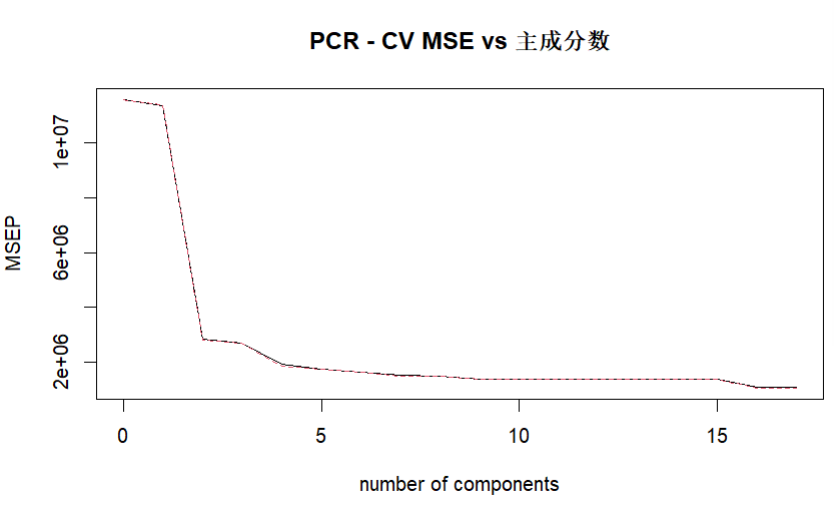
mse_vals_pcr <- MSEP(pcr_model)$val[1, 1, ]
delta_mse_pcr <- diff(mse_vals_pcr)# 打印每一步下降的幅度： 选择肘点
for (i in 1:length(delta_mse_pcr)) {cat(sprintf("从 %d 到 %d 主成分，MSE 下降：%.4f\n", i, i+1, delta_mse_pcr[i]))
}

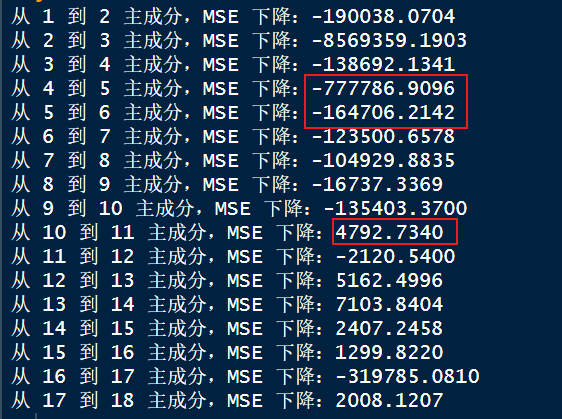
在此次测试中，我选用了肘点，并非使用min mse 对应的主成分数

由此可知可选用的主成分数为 4 or 5 

pred_pcr <- predict(pcr_model, newdata = test, ncomp = 4)  
rmse_pcr <- sqrt(mean((pred_pcr - test$Apps)^2))
rmse_pcr # 2179.3

3.2 偏最小二乘回归 PLS

 偏最小二乘回归 PLS
pls_model <- plsr(Apps ~ ., data = train, scale = T, validation = "CV")

        PLS 在预测时依然需要确定主成分个数，因此需要确定最佳主成分个数

# 可视化验证误差随成分数的变化
validationplot(pls_model, val.type = "MSEP", main = "PLS: MSEP vs 主成分数")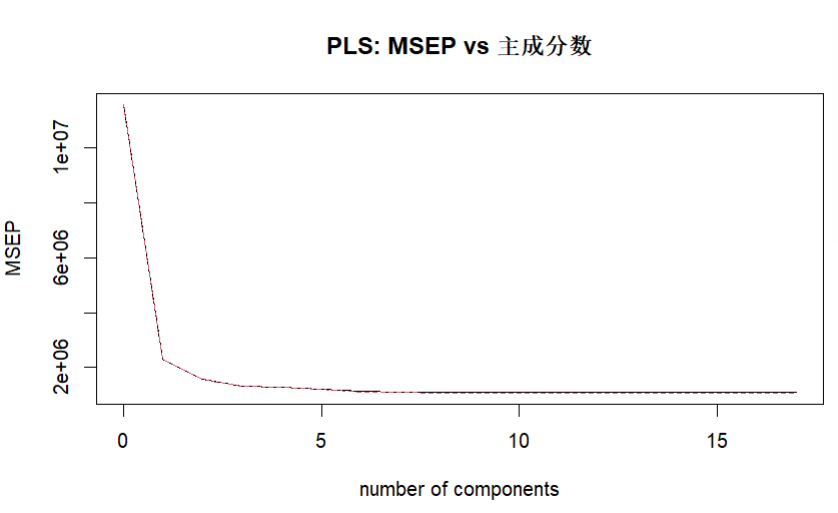

mse_vals_pls <- MSEP(pls_model)$val[1,1,-1]  # 去掉截距项
delta_mse_pls <- diff(mse_vals_pls)
for (i in 1:length(delta_mse_pls)) {cat(sprintf("从 %d 到 %d 主成分，MSE 下降：%.4f\n", i, i+1, delta_mse_pls[i]))
}# 使用推荐主成分数进行预测
pred_pls <- predict(pls_model, newdata = test, ncomp = 6)
# 计算均方误差
rmse_pls <- sqrt(mean((pred_pls - y_test)^2))
cat("PLS 模型的 RMSE 为：", rmse_pls, "\n")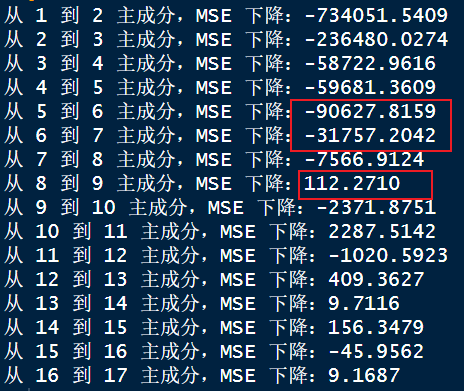

 

由此可知可选用的主成分数为 6 or 7

# 使用推荐主成分数进行预测
pred_pls <- predict(pls_model, newdata = test, ncomp = 6)
# 计算均方误差
rmse_pls <- sqrt(mean((pred_pls - y_test)^2))
cat("PLS 模型的 RMSE 为：", rmse_pls, "\n") # 1361.724

 四、模型比较

模型模型RMSE
回归模型线性回归1317.134
逐步回归（b）1309.17
岭回归1725.214
LASSO回归1315.667
Elastic Net 回归1335.79
树模型决策树2479.202
随机森林2348.264
XGBoost2151.398
降维PCR2179.3
PLS1361.724 

由此可知回归模型整体的拟合度较高

http://www.dtcms.com/a/304596.html

相关文章：

  • 《React与Vue构建TODO应用的深层逻辑》
  • 【lucene】SegmentCoreReaders
  • linux_前台，后台进程
  • LeetCode热题100——155. 最小栈
  • (LeetCode 面试经典 150 题) 150. 逆波兰表达式求值 （栈）
  • 电脑主机显示的python版本是3.8.6，但是我在控制面板没有找到，想删除不知道怎么操作怎么办
  • 《 java 随想录》| LeetCode链表高频考题
  • 【LeetCode】大厂面试算法真题回忆(111)--身高排序
  • 鱼皮项目简易版 RPC 框架开发（五）
  • 2.oracle保姆级安装教程
  • 逐渐走进Ai世界~
  • Django模型开发：模型字段、元数据与继承全方位讲解
  • Unity_SRP Batcher
  • 【WRF-Chem 实例1】namelist.input 详解- 模拟CO2
  • 基于AI代码疫苗技术的开源软件供应链安全治理
  • C# _列表（List＜T＞）_ 字典（Dictionary＜TKey, TValue＞）
  • 【dropdown组件填坑指南】—怎么实现下拉框的位置计算
  • 【机器学习深度学习】为什么需要分布式训练？
  • 从硬编码到自主智能体：营销AI的20年技术演进与未来展望
  • 前端开发为什么没有后端开发那么清除业务
  • sqLite 数据库 (2)：
  • 摔倒识别误报率↓79%：陌讯动态时序融合算法实战解析
  • System V IPC机制：进程通信的统一设计
  • 单片机（STM32-WIFI模块）
  • 【JavaScript】手写 Object.prototype.toString()
  • Qt 移动应用常见问题与解决方案
  • React服务端渲染 Next 使用详解
  • 安卓模拟器 adb Frida hook 抓包
  • Ubuntu第一步——下载、网络、apt
  • 用系统架构思维，告别“意大利面条式”系统提示词