递归、搜索与回溯算法核心思想解析

14.找出所有子集的异或总和再求和

题目链接
一个数组的 异或总和 定义为数组中所有元素按位 XOR 的结果；如果数组为 空 ，则异或总和为 0 。

• 例如，数组 [2,5,6] 的 异或总和 为 2 XOR 5 XOR 6 = 1 。

给你一个数组 nums ，请你求出 nums 中每个 子集 的 异或总和 ，计算并返回这些值相加之 和 。

注意： 在本题中，元素 相同 的不同子集应 多次 计数。

数组 a 是数组 b 的一个 子集 的前提条件是：从 b 删除几个（也可能不删除）元素能够得到 a 。

示例 1：

输入： nums = [1,3]
输出： 6
解释：[1,3] 共有 4 个子集：

• 空子集的异或总和是 0 。
• [1] 的异或总和为 1 。
• [3] 的异或总和为 3 。
• [1,3] 的异或总和为 1 XOR 3 = 2 。
  0 + 1 + 3 + 2 = 6

示例 2：

输入： nums = [5,1,6]
输出： 28
解释：[5,1,6] 共有 8 个子集：

• 空子集的异或总和是 0 。
• [5] 的异或总和为 5 。
• [1] 的异或总和为 1 。
• [6] 的异或总和为 6 。
• [5,1] 的异或总和为 5 XOR 1 = 4 。
• [5,6] 的异或总和为 5 XOR 6 = 3 。
• [1,6] 的异或总和为 1 XOR 6 = 7 。
• [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
  0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

示例 3：

输入： nums = [3,4,5,6,7,8]
输出： 480
解释： 每个子集的全部异或总和值之和为 480 。

每次枚举到一个数据，我们就异或到path中去，然后进入到下一层去

class Solution{int path;int sum;public:int subsetXORSum(vector<int>& nums){dfs(nums,0);return sum;}void dfs(vector<int>&nums,int pos){sum+=path;for(int i=pos;i<nums.size();i++){path^=nums[i];dfs(nums,i+1);path^=nums[i];//恢复现场，就是重复异或两个相同的数，达到消除这个数的效果}}};

假设nums = [1, 2]，过程如下：

1. 在第一个递归调用时，path的值初始化为0。加入元素1，path ^= 1，现在path = 1。
2. 继续递归并加入元素2，path ^= 2，现在path = 3。
3. 回溯到上一级，撤销对path的改变，执行path ^= 2，恢复path为1（恢复现场）。
4. 继续探索下一个子集，执行path ^= 1，恢复path为0（恢复现场）。

通过这种方式，每次递归的path值都是独立计算的，不会受到其他递归分支的影响。

因此，“恢复现场”是为了确保在递归结束后path的值能够恢复到递归调用前的状态，防止影响后续的递归逻辑。

15.全排列 II

题目链接
示例 1：

输入： nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入： nums = [1,2,3]
输出： [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1] ]


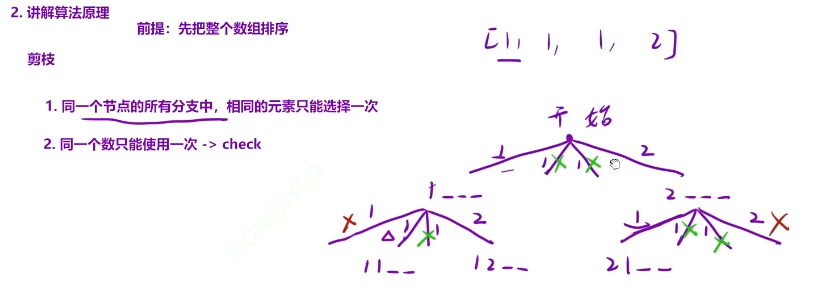
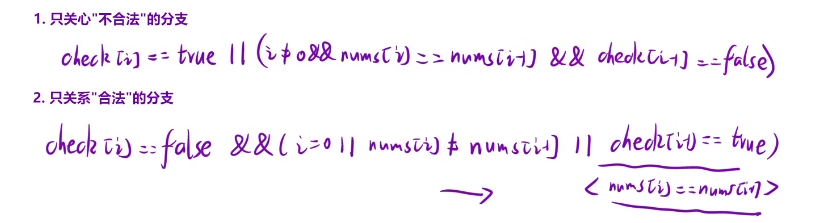
我们下面这种代码的策略就是只关心不合法的分支

class Solution{vector<vector<int>>ret;//记录最终结果vector<int>path;//记录路径bool check[9];//记录当前这个数是否已经被使用过了public:vector<vector<int>> permuteUnique(vector<int>& nums){sort(nums.begin(),nums.end());dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos==nums.size())//边界条件{ret.push_back(path);//将当前的路径添加到ret中去return ;}for(int i=0;i<nums.size();i++){//剪枝//如果我们当前的这个数字是用过的，并且前一个数和这数是相等的而且是没有用过的，我们直接跳过此次循环进行下一次循环if(check[i]==true||(i!=0&&nums[i]==nums[i-1]&&check[i-1]==false))continue;//说明我们此时的i位置是不合法的，我们需要跳过这个位置path.push_back(nums[i]);//我们将这个数放到路径中去check[i]=true;//修改我们这个数的一个状态dfs(nums,pos+1);//进入到下一个位置path.pop_back();//回溯后将这个路径中的最后一个数据删除掉check[i]=false;}}};

这里我们就是考虑的符合要求的条件，

class Solution{vector<vector<int>>ret;//记录最终结果vector<int>path;//记录路径bool check[9];//记录当前这个数是否已经被使用过了public:vector<vector<int>> permuteUnique(vector<int>& nums){sort(nums.begin(),nums.end());dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos==nums.size())//边界条件{ret.push_back(path);//将当前的路径添加到ret中去return ;}for(int i=0;i<nums.size();i++){//剪枝//如果我们这个数是没有使用过的，在这个前提下，我们的i=0或者是和前面的数不相等或者是虽然和前面的数相等，但是前面的值没有使用过if(check[i]==false&&(i==0||nums[i]!=nums[i-1]||check[i-1]!=false)){path.push_back(nums[i]);//我们将这个数放到路径中去check[i]=true;//修改我们这个数的一个状态dfs(nums,pos+1);//进入到下一个为止path.pop_back();//回溯后将这个路径中的最后一个数据删除掉check[i]=false;}}}};

16.电话号码的字母组合

题目链接
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入： digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

示例 2：

输入： digits = “”
输出：[]

示例 3：

输入： digits = “2”
输出：[“a”,“b”,“c”]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

我们只需要进行一次深度优先遍历，然后在叶子节点获取我们的结果就行了

class Solution{string hash[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};string path;//记录路径vector<string>ret;//返回结果public:vector<string> letterCombinations(string digits){if(digits.size()==0)return ret;//空字符串直接返回空的就行了dfs(digits,0);//从0位置开始翻译操作return ret;}void dfs(const string& digits,int pos)//不修改的前提下加个const和&减少拷贝{if(pos==digits.size())//越界了，就说明我们遍历到叶子节点了{ret.push_back(path);//将当前路径加入到返回结果中return ;}for(auto ch:hash[digits[pos]-'0'])//直接找出对应的字符所代表的字母{path.push_back(ch);//将每一次的字符加入到path之中去dfs(digits,pos+1);//去pos+1的位置去找path.pop_back();//恢复现场}}};

• 终止条件：当 pos == digits.size() 时，表示已经遍历完整个数字字符串，达到了叶子节点。此时将当前路径 path（即一个字母组合）添加到结果 ret 中。
• 递归部分：对于 digits[pos] 这个数字，找出它对应的字母（通过 hash[digits[pos] - '0']）。然后，将每一个字母加入 path 中，并递归调用 dfs 去处理下一个数字。
• 恢复现场：每次递归结束后，path.pop_back() 会把最后添加的字母移除，恢复到上一个状态，以便进行下一个字母的尝试。

17.括号生成

题目链接

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入： n = 3
输出： [“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]

示例 2：

输入： n = 1
输出： [“()”]

有效的括号组合？
1.左括号的数量=右括号的数量
2.从头开始的任意一个子串，左括号的数量>=右括号的数量

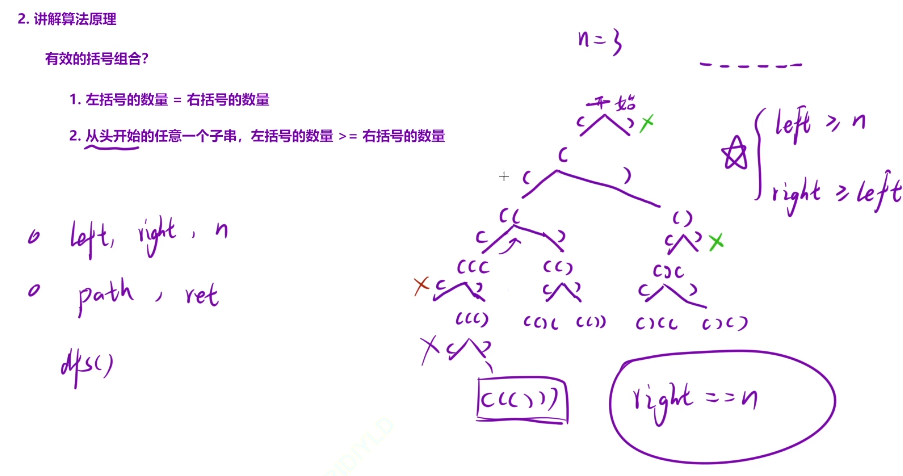
class Solution{int left,right,_n;string path;vector<string>ret;public:vector<string> generateParenthesis(int n){_n=n;dfs();return ret;}void dfs(){if(right==_n){ret.push_back(path);//当我们的右括号等于我们的n的时候，我们就到了叶子节点了，可以将路径添加到返回结果了return ;}if(left<_n)//添加左括号，直到我们的左括号的数量到达n{path.push_back('(');left++;//进行数量的统计操作dfs();//然后去下一层添加左括号path.pop_back();left--;//回溯，删除我们路径中的最后一个元素，并且进行数量的重新统计操作}if(right<left)//添加右括号{path.push_back(')');right++;//进行数量的统计操作dfs();//然后去下一层添加左括号path.pop_back();right--;//回溯，删除我们路径中的最后一个元素，并且进行数量的重新统计操作}}};

• • 终止条件：当 right == _n 时，表示当前组合已经生成了足够的右括号，并且这个组合是有效的，可以将其加入结果 ret 中。
    • 递归生成左括号：
      • 如果 left < _n，表示我们还可以继续添加左括号 (，就将 ( 加入到路径 path 中，更新 left 数量，并递归调用 dfs 生成下一层的组合。
      • 回溯时，弹出路径中的最后一个 (，恢复 left 的数量，继续尝试其他的可能性。
    • 递归生成右括号：
      • 如果 right < left，表示右括号 ) 的数量不能超过左括号 ( 的数量，我们可以添加右括号 )，将其加入路径 path 中，更新 right 数量，并递归调用 dfs 生成下一层的组合。
      • 同样地，回溯时，弹出路径中的最后一个 )，恢复 right 的数量，继续尝试其他的可能性。
• 回溯：递归的关键在于回溯（pop_back() 和数量恢复）。每次递归添加一个括号后，都需要进行回溯，以便尝试下一个可能的括号。

假设 n = 3，即需要生成 3 对括号。

• 初始时 left = 0, right = 0，路径为空 path = ""。
• 可以选择添加左括号 (，此时路径变成 path = "("，left = 1，继续递归。
• 继续添加左括号 (，路径变成 path = "(("，left = 2，继续递归。
• 继续添加左括号 (，路径变成 path = "((("，left = 3，此时左括号已经达到上限，可以开始添加右括号 )。
• 添加右括号 )，路径变成 path = "((()"，right = 1，继续递归。
• 继续添加右括号 )，路径变成 path = "((())"，right = 2，继续递归。
• 再添加右括号 )，路径变成 path = "((()))"，right = 3，此时左括号和右括号的数量都已达到 3，此时为一个有效的括号组合，可以将其加入结果 ret 中。
• 然后进行回溯，尝试其他组合，最终得到所有的有效括号组合。