散列表（哈希表）

散列表介绍

        散列表（hash table，又称哈希表），是一种数据集，其中数据项的存储方式尤其有利于将来快速的查找定位。

        散列表的基本思想是，首先在关键字key和存储位置p之间建立一个对应关系H，使得p = H(key),H称为哈希函数，p称为散列地址。当创建哈希表时，把关键字key的记录直接存入地址为H(key)的地址单元中；以后查找关键字为key的元素时，再利用哈希函数p = H(key)计算出该元素的散列地址p，从而达到直接存取记录的目的。因此，该方法的核心就是由哈希函数决定关键字值与散列地址之间的对应关系，通过这种关系来组织存储并进行查找等操作。

散列函数（哈希函数）的构造方法

        哈希函数的构造方法主要有两种：直接定址法和除数留余法。

直接定址法

        下面这种构造映射关系的方法是直接定址法，H(key)=key。

        假如关键字变为了100-105，那么对应的下标要用105个大小的数组吗？这样用105个大小的数组存储6个数据未免太浪费，那么我们可以更改散列函数为H(Key) = Key - 100。所以直接定址法的散列函数一般为H(key) = a * key + b;适合关键字基本连续的情况。 

除数留余法

        如果遇到关键字不连续的情况，再使用直接定址法会造成很大的空间浪费。若关键字分别为42 36 89 3 13 67，仅有六个数据，但是关键字分布杂乱，不连续，如果使用直接定址法，那么就需要0-89共90个存储空间。

        此时可以使用除留余数法：H(key) = key % p，这样求余操作可以把不连续的关键字映射到连续的地址空间。p一般取小于等于表长的最大质数，这样设置可以使发生冲突的概率变小，冲突就是多个关键字映射到了同一个下标上，这些映射到同一下标的多个关键字称为同义词，比如当p取5时，对5取余，如果要插入关键字为14和19的两个元素，19和17对5取余得到的散列地址都是4，都映射到了同一个下标上，但是同一个数组下标又无法同时存储两个数据。这种情况会影响散列表的性能，冲突越多，散列表的效率越低，但是冲突是无法避免的，只能尽量减少冲突。

        例如关键字分别为42 36 89 3 13 67，要存储这几个元素，表长最小为6，结合p要取小于等于表长的最大质数，所以最终表长定为7，p为7。最终插入结果如下图所示，由于还没有介绍处理冲突的方法，此处选用的关键字都是没有发生冲突的情况。

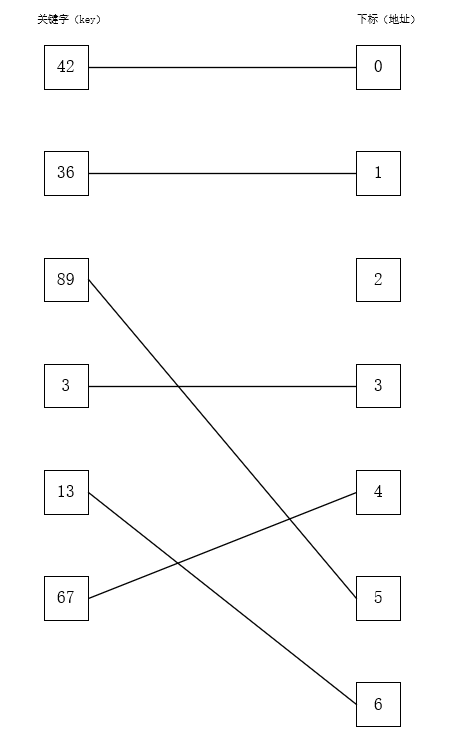
        还有另外一个参数会影响散列表的性能：空间利用率，也叫装填因子。装填因子等于表中元素个数/表的长度，装填因子越大，发生冲突的可能性越大；装填因子越小，发生冲突的可能性就越小，但是空间利用率就低，容易浪费很多空间。

两种方法的比较

	直接定址法	除数留余法
主要形式	H(key) = a * key + b	H(key) = key % p (p一般取小于等于表长的最大质数)
适合情况	关键字分布连续的情况	任何情况，可以把不连续的关键字映射到连续的地址空间
是否会出现冲突	永远不会出现冲突	会出现冲突
空间利用率	低	强

处理冲突的方法

        影响散列表性能的因素除了散列函数，装填因子之外，处理冲突的方法也限制了散列表的性能。

        在发生冲突时我们会采用不同的处理冲突的方法，一般分为两种：开放定址法和拉链法，两种方法下的查找、删除操作都有不同的思路和实现，要特别区分，在进行查找、删除操作时一定要区分使用的是哪种冲突处理方法。

开放定址法

        在发生冲突时，为发生冲突的关键字2找一个新的位置来存储，这就是开放定址法。最简单的开放定址法的思路是线性探测法：在发生冲突后，依次探测后一个位置，直到遇见空闲位置。注意表尾的下一个位置是表首。

        例如将19 8 15 65 98 49 37 26使用除数留余法+线性探测法构造哈希表，要求装填因子为0.8.

装填因子等于元素个数 / 表长，那么表长就等于元素个数 / 装填因子，所以表长取为10，p取小于等于表长的最大质数，为7。然后开始按散列函数逐个将元素插入到对应的下标地址上：19%7为5，插入到下标5；8%7为1，插入到下标1；15%7为1，发生冲突，按线性探测法规则，继续查看下标2，下标2空闲，插入到下标2；65%7为2，发生冲突，继续查看下标3，下标3空闲，插入下标3；98%7为0，插入下标0；49%7为0，发生冲突，查看下标1，仍然冲突，继续向后查看，直到下标4空闲，插入下标4；37%7为2，发生冲突，逐个向后查看直到下标6空闲，插入下标6；26%7为5，发生冲突，向后探查直到下标7空闲，插入到下标7。最终插入结果如下图

typedef struct hash_list
{int *data;  //存储结构int length; //哈希表总长度int p;      //除数int size;   //哈希表当前元素个数
}hash_list;hash_list *hash_init(int length,int p)
{//分配结构体大小hash_list *hash = (hash_list *)malloc(sizeof(struct hash_list));//赋值哈希表总长度hash->length = length;//分配元素存储空间hash->data = (int *)malloc(sizeof(int) * length);//设置除数hash->p = p;//初始化哈希表当前元素个数hash->size = 0;//将哈希表数据初始化为0，代表空位置memset(hash->data,0,hash->length);return hash;
}
void hash_insert(hash_list *hash,int data)
{//判断哈希表是否满if(hash->size == hash->length)return;//通过哈希函数得到散列地址int i = data % hash->p;//若此处不为0或-1代表发生冲突，线性探测法向后查看while (hash->data[i] != 0 && hash->data[i] != -1){//防止数组溢出i = (i + 1) % hash->length;}//插入元素hash->data[i] = data;//当前元素个数+1hash->size++;
}

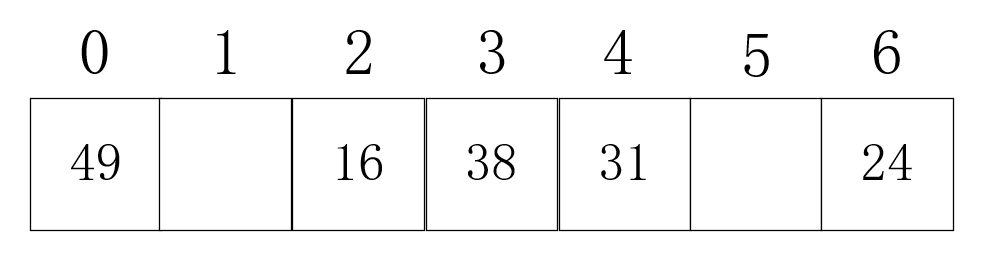
        开放定址法的另外一个思路就是平方探测法：发生冲突时按照+1²，-1²，+2²，-2²的顺序进行探测。这种方法的好处是可以缓解堆积问题，缺点就是由于是跳跃性的，不一定能探测到所有散列表位置。但是当表长为某个4k+3的质数时，那么就一定可以探测到所有位置。所以采用平方探测法时一般会按这个规则设置表长。例如要存16 38 49 31 24五个元素，那么使k为1，表长为7即可。

        下面详细说明插入过程：构造方法依然采用除数留余法，p=7。16%7为2，插入到下标2；38%7为3，插入到下标3；49%7为0，插入到下标0；31%7为3，发生冲突，按照顺序，先+1²，3+1²为4，插入下标4；24%7为3，发生冲突，3+1²为4，仍然冲突，3-1²为2，仍然冲突，3+2²为7，发生溢出，实则为下标0，仍然冲突，3-2²为-1，，发生溢出，实则为下标6，插入下标6。最终插入结果如下图：

 哈希表的查找

        此时如果我们需要查找一个数，依旧是按照散列函数对关键字进行映射，之后查看映射到的下标地址上的元素和要查找的数是否相同，如果不相同则继续向下一个位置查找，也就是插入时使用的线性探测法，直到找到。若要查找的数并不在散列表内，那么在使用线性探测法时，在移动之后就可能会碰到空元素，例如上述下标为1 5的地方就是空元素，遇见空元素就可以判定要查找的数不在散列表内。因为假如该数在散列表内，那么按照相同的映射关系和相同的线性探测法已经插入了，在查找时一定不会遇见空元素。

        空元素虽然被称为空元素，但位置上肯定会有数据的，一般我们会定义一个值为空位置的标记，比如如果这个下标是空的，那么就给他赋值为0，代表这是个空位置，但是要注意，这个标记值不能和关键字重复，防止混乱。

        我们在查找元素时也需要检查一下查找的次数，防止死循环。例如总表长为10，将所有元素全部插入之后又全部删除，此时所有位置都是删除标记，我们在查找时在遇见空位置标记才会停止，如果不限制查找次数，就会导致死循环。

//返回-1表示查找失败，返回0以上的值代表元素所在下标
int hash_find(hash_list *hash,int data)
{//若哈希表为空则停止查找if(hash->size == 0)return -1;//通过哈希函数得到散列地址int i = data % hash->p;int step = 0;//探测步数while (1){//若探测到空位置则代表元素不存在//当已经探测了表中的所有位置时，如果还没有探测到，那么就查找失败if(hash->data[i] == 0 || step >= hash->length)return -1;//查找到数据后返回所在下标地址if(hash->data[i] == data)break;//防止数组溢出i = (i + 1) % hash->length;//探测步数+1step++;}//返回该元素所在下标return i;
}

哈希表的删除

        如果我们要删除一个元素比如上图中的38，不能直接删除，因为删除之后，下标3处变为一个空位置，那么就会阻断后续数据的查找。比如删除之后要查找31，那么会从下标3开始，之后用线性探测法逐个比较，在下标3遇见了空位置，就会认为31这个元素不存在，但是实际上31是存在的。

        为了防止这种情况，我们可以再定义一个删除标记，代表这个位置不是空的，而是被删除的，删除元素之后在其位置打上删除标记。这样我们查找时只在遇见空位置时结束，碰见删除标记还会继续探测。注意删除标记也不能与空标记、关键字重复。一般可以设定空标记为0，删除标记为-1。

        定义了删除标记后，我们在进行插入操作时就需要额外判断一次，因为空位置可以插入，删除标记的位置同样也可以插入。比如删除38之后再插入一个元素45，此时映射到下标3处，发现下标3处被打上了删除标记，那么就可以插入到下标3处。

void hash_delete(hash_list *hash,int data)
{//若哈希表为空则返回if(hash->size == 0)return;//查找该元素所在地址int tmp = hash_find(hash,data);//若未查到则返回if(tmp == -1)return;//打上删除标记hash->data[tmp] = -1;//当前元素个数-1hash->size--;
}

拉链法

        拉链法的基本思想是将所有冲突的同义词用一个单链表串起来，以前是为发生冲突的关键字重新寻找新的位置，现在是把他们用链表串在一起。

        如果采用拉链法的话，那么数组中存储的就不是关键字了，而是链表的头指针，此时就变为了一个指针数组，当该位置为空时，存储的就是NULL。此时，删除和插入操作就成了对链表的插入和删除，构造方法还是选择除数留余法最好。

        例如将一些数据采用拉链法，除数留余法插入到链表中，结果如下。

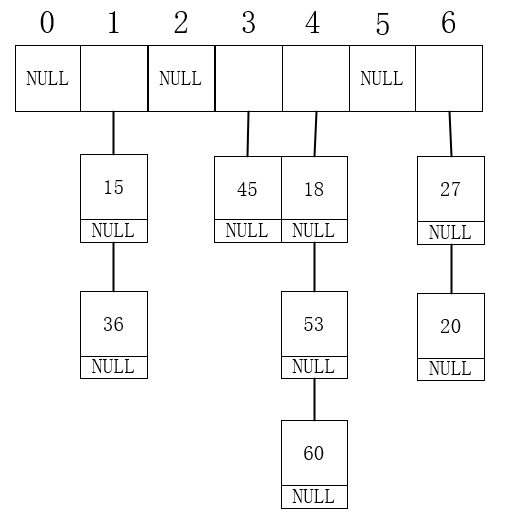
typedef struct node
{int data;struct node *next;
}Node;typedef struct hash
{struct node **Node; //指针数组，存放链表的头结点int point_length;   //链表个数int size;           //当前元素个数int p;              //除数
}hash_list;void list_head_insert(Node *list,int data)
{//为新结点分配内存Node *new_node = (Node *)malloc(sizeof(Node));//新结点赋值new_node->data = data;//新结点就是新的首元结点new_node->next = list->next;//更新头指针的后继指针list->next = new_node;
}hash_list *hash_init(int point_length,int p)
{hash_list *hash = (hash_list *)malloc(sizeof(struct hash));//为数组分配容纳point_length个指针的内存hash->Node = (struct node **)malloc(sizeof(struct node *) * point_length);hash->point_length = point_length;hash->size = 0;hash->p = p;for (int i = 0; i < point_length; i++){//为指针数组的每个元素分配内存，初始化每个链表的头结点hash->Node[i] = (struct node *)malloc(sizeof(struct node));hash->Node[i]->data = 0;hash->Node[i]->next = NULL;}return hash;
}void hash_insert(hash_list *hash,int data)
{//得到散列地址int i = data % hash->p;//链表插入list_head_insert(hash->Node[i],data);hash->size++;
}

哈希表的查找

        在拉链法情况下的查找思路是：通过散列函数映射到下标地址，然后根据从存放的链表头指针开始进行顺序查找。若元素存在肯定不必多说；若查找过程中碰到了NULL，那就说明查找已经到头了，没有查找到，所以元素不存在。 

Node *hash_find(hash_list *hash,int data)
{//得到散列地址int i = data % hash->p;Node *current = hash->Node[i]->next;while (current != NULL && current->data != data){current = current->next;}return current;
}

哈希表的删除

        在拉链法情况下删除元素是可以直接删除掉的，不用打删除标记。原因有如下两点：

        1、之前打删除标记是为了不阻断其他元素的查找路径，但是拉链法下的查找路径是单链表的路径，并不会被其他元素阻挡。

        2、之前打删除标记是为了告诉我们此处可以插入元素，但是拉链法下的插入操作在任何位置都是可以进行的，所以不需要特殊标记。

bool list_delete(Node *list,int data)
{//定义双指针，当前结点和前驱结点Node *current = list->next;Node *pre = list;while (1){//链表到头，则没有这个元素if(current == NULL)return false;//查找到了这个元素，跳出循环if(current->data == data)break;//更新前驱指针pre = current;//更新当前指针current = current->next;}//更新前驱指针的后继指针域pre->next = current->next;//释放当前指针free(current);return true;
}void hash_delete(hash_list *hash,int data)
{//得到散列地址int i = data % hash->p;//删除链表结点if(list_delete(hash->Node[i],data))hash->size--;
}void hash_free(hash_list *hash)
{Node *current;Node *tmp;//释放指针数组中每个链表的内存for (int i = 0; i < hash->point_length; i++){current = hash->Node[i];while (current){tmp = current;current = current->next;free(tmp);}}//释放指针数组的内存free(hash->Node);//释放哈希表结构体的内存free(hash);
}